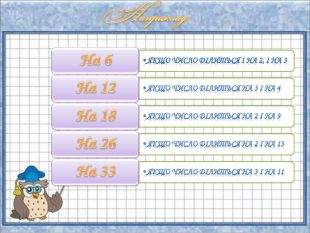
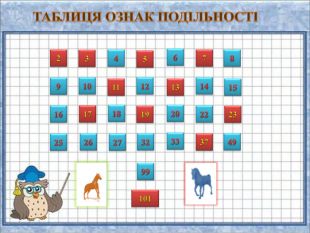
Презентація "Ознаки подільності натуральних чисел"

Мета дослідження: доведення основних ознак подільності натуральних чисел, наведення прикладів їх застосування для встановлення подільності одного числа на інше, а також при розв’язуванні задач підвищеної складності на доведення подільності чисел, або ж на знаходження остачі від ділення чисел, яку звичним способом знайти практично неможливо.

Ознакою подільності називається правило, за допомогою якого можна встановити подільність одного числа на друге, не виконуючи ділення.

ДОВЕДЕННЯ ОЗНАКИ ПОДІЛЬНОСТІ НА 7

Ознака подільності на 7 Якщо сума числа без останньої цифри і останньої цифри, помноженої на 5, ділиться на 7.36436 + (5×4) = 56. 56 ділиться на 7.ppt_x

Ознака подільності на 7 Різниця між числом без останньої цифри і подвоєної останньої цифри повинна ділитись на 7.36436 − (2×4) = 28. 28 ділиться на 7.ppt_x

Ознака подільності на 7 Якщо сума подвоєного числа без останніх двох цифр і останніх двох цифр ділиться на 7.364 (3x2) + 64 = 70. 70 ділиться на 7.ppt_x

Ознака подільності на 7 Число розбивається на блоки по три цифри, починаючи з кінця. Число ділиться на 7, якщо різниця суми блоків, що стоять на парних місцях, і суми блоків, що стоять на непарних місцях, ділиться на 72 911 272911 - (2 + 272) = 637. 637 ділиться на 7ppt_x

На 11 діляться числа, у яких сума цифр, що займають непарні місця, або дорівнює сумі цифр, що займають парні місця, або відрізняється від неї на число, яке ділиться на11. Ознака подільності на 11

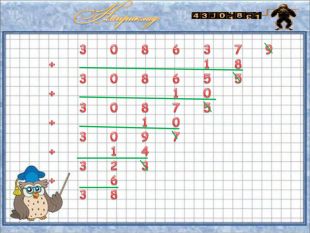
Число 9 163 627 ділиться на 11, тому що різниця між сумою цифр,що займають непарні місця (9+6+6+7=28), і сумою цифр, що займають парні місця (1+3+2=6), дорівнює 22, яке ділиться на 11. Число 461 025 не ділиться на 11, оскільки суми цифр, що займають непарні і парні місця (4+1+2=7, 6+0+5=11), не дорівнюють одна одній та їх різниця (11-7=4) не ділиться на 11.ppt_x

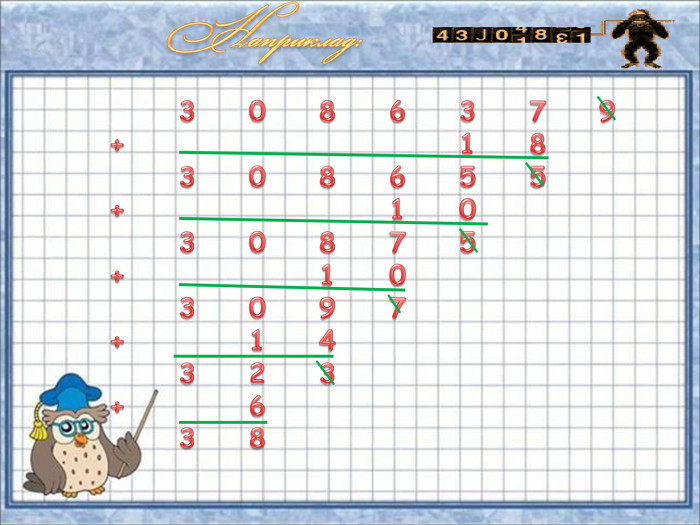
Ознака подільності на 19 Розглянемо ознаку подільності на 19, запропоновану студентом коледжу із Східної Африки Казангакі. Цей метод полягає у тому, що для з'ясування подільності числа N на 19 треба закреслити останню цифру цього числа і до числа, що залишилось, додати подвоєну викреслену цифру. Якщо здобуте таким чином число ділиться на 19, то задане число N теж ділиться на 19.

3 0 8 6 3 7 9+ 1 8 3 0 8 6 5 5 + 1 0 3 0 8 7 5 + 1 0 3 0 9 7 + 1 4 3 2 3 + 6 3 8 ppt_x

38 ділиться на 19. Отже, 3 086 379 ділиться на 19.

Число ділять на блоки по три цифри, починаючи з кінця. Числа, утворені блоками сумують. Сума повинна ділитись на 37. Ознака подільності на 37

2 651272925++=925 ділиться на 37. Отже, 2 651 272 ділиться на 37.ppt_x

ОЗНАКИ ПОДІЛЬНОСТІ НА СТЕПІНЬ 2, 5,10

ОЗНАКИ ПОДІЛЬНОСТІ НА СТЕПІНЬ 2, 5,10

ОЗНАКИ ПОДІЛЬНОСТІ НА СТЕПІНЬ 2, 5,10

ОЗНАКИ ПОДІЛЬНОСТІ НА СТЕПІНЬ 2, 5,10

ОЗНАКИ ПОДІЛЬНОСТІ НА СТЕПІНЬ 2, 5,10

ОЗНАКИ ПОДІЛЬНОСТІ НА СТЕПІНЬ 2, 5,10

Ознака подільності на 99 Розіб'ємо число на групи по 2 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп, вважаючи їх двозначними числами. Ця сума ділиться на 99 тоді і тільки тоді, коли саме число ділиться на 99.ppt_xppt_x

Ознака подільності на 101 Розіб'ємо число на групи по 2 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп із змінними знаками, вважаючи їх двозначними числами. Ця сума ділиться на 101 тоді і тільки тоді, коли саме число ділиться на 101.

-+=ppt_x

Якщо с ділиться а і с ділиться b, то с ділиться ab, якщо a і b взаємно прості. На основі цієї властивості можна встановити ознаки подільності за множниками дільника, якщо вони взаємно прості числа.

ppt_x

ТЕОРЕМА ФЕРМА17 серпня 1601 — 12 січня 1665 style.colorfillcolorfill.type

ppt_x

ТАБЛИЦЯ ОЗНАК ПОДІЛЬНОСТІ 23747810121113151416182019172227263225334923991016935

ТАБЛИЦЯ ПОДІЛЬНОСТІ ЧИСЕЛ

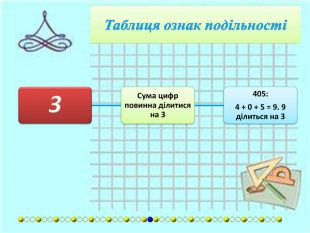
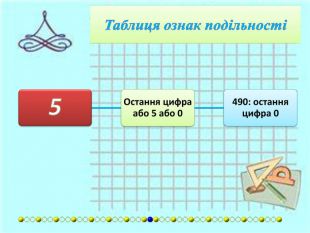
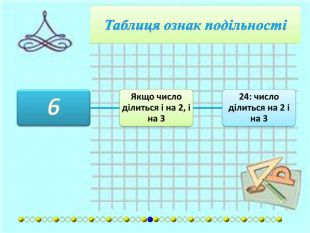
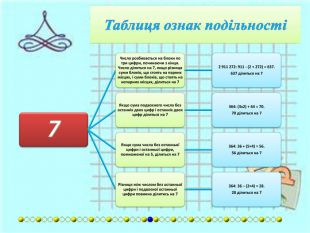
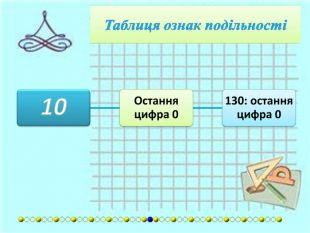
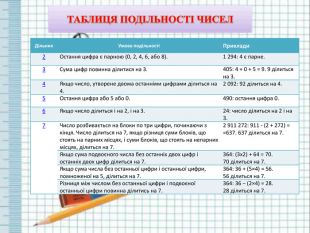
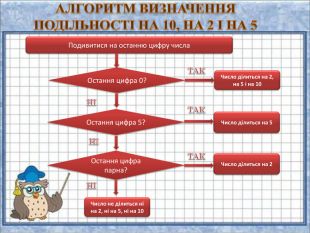
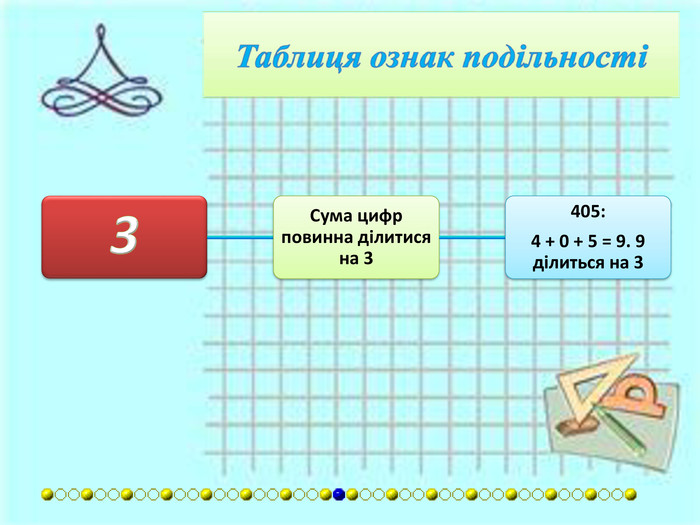
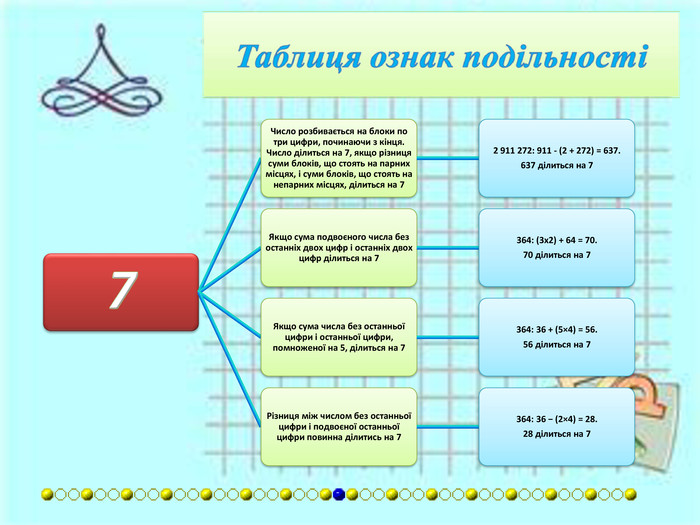
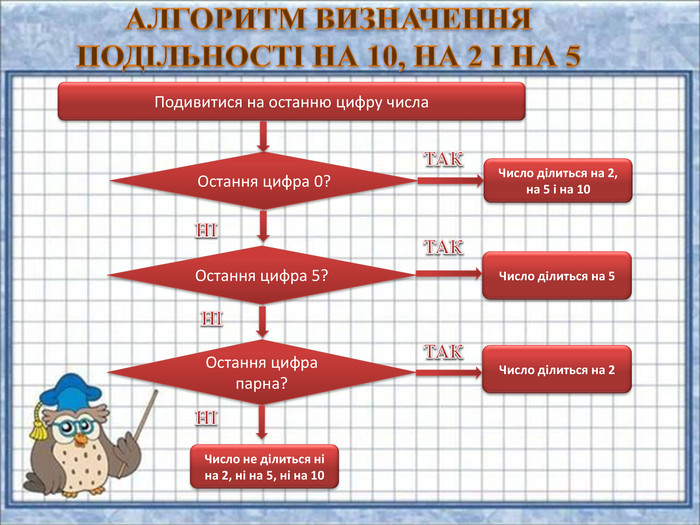
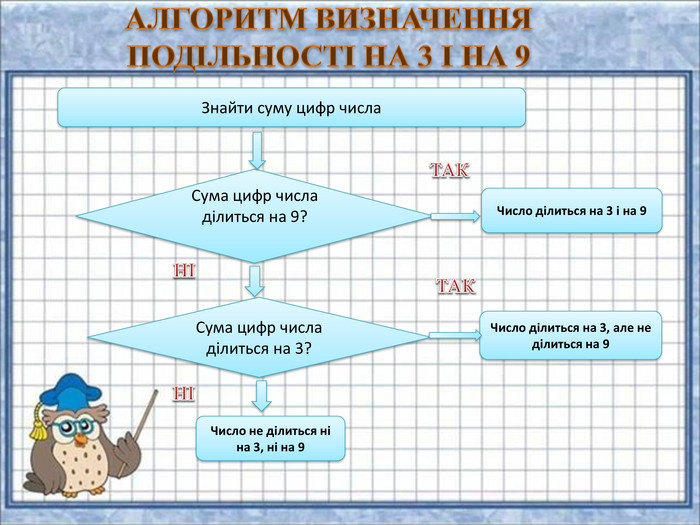
{FABFCF23-3 B69-468 F-B69 F-88 F6 DE6 A72 F2}Дільник. Умова подільностіПриклади2 Остання цифра є парною (0, 2, 4, 6, або 8).1 294: 4 є парне.3 Сума цифр повинна ділитися на 3.405: 4 + 0 + 5 = 9. 9 ділиться на 3.4 Якщо число, утворене двома останніми цифрами ділиться на 4.2 092: 92 ділиться на 4.5 Остання цифра або 5 або 0.490: остання цифра 0.6 Якщо число ділиться і на 2, і на 3.24: число ділиться на 2 і на 3.7 Число розбивається на блоки по три цифри, починаючи з кінця. Число ділиться на 7, якщо різниця суми блоків, що стоять на парних місцях, і суми блоків, що стоять на непарних місцях, ділиться на 7.2 911 272: 911 - (2 + 272) = =637. 637 ділиться на 7. Якщо сума подвоєного числа без останніх двох цифр і останніх двох цифр ділиться на 7.364: (3x2) + 64 = 70. 70 ділиться на 7. Якщо сума числа без останньої цифри і останньої цифри, помноженої на 5, ділиться на 7.364: 36 + (5×4) = 56. 56 ділиться на 7. Різниця між числом без останньої цифри і подвоєної останньої цифри повинна ділитись на 7.364: 36 − (2×4) = 28. 28 ділиться на 7.

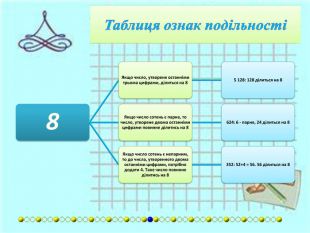
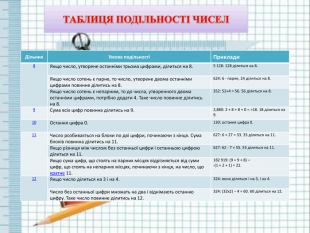
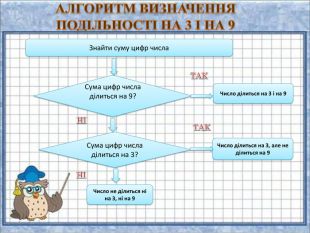
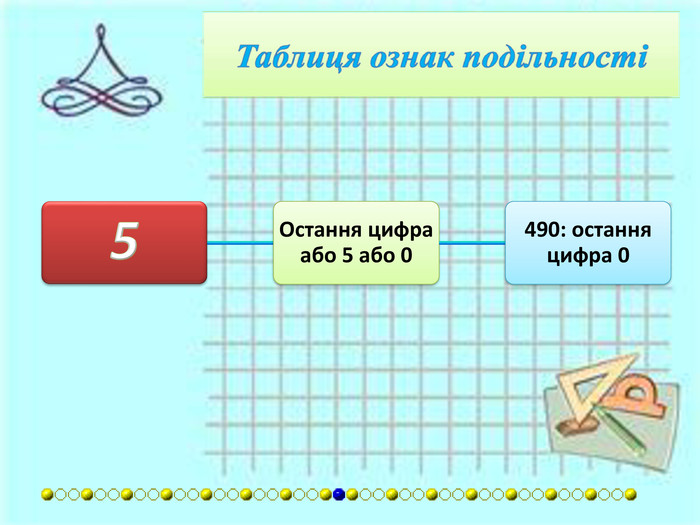
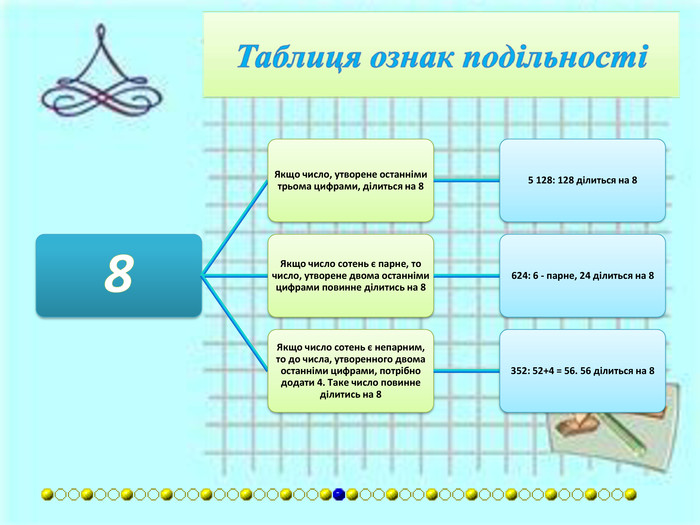
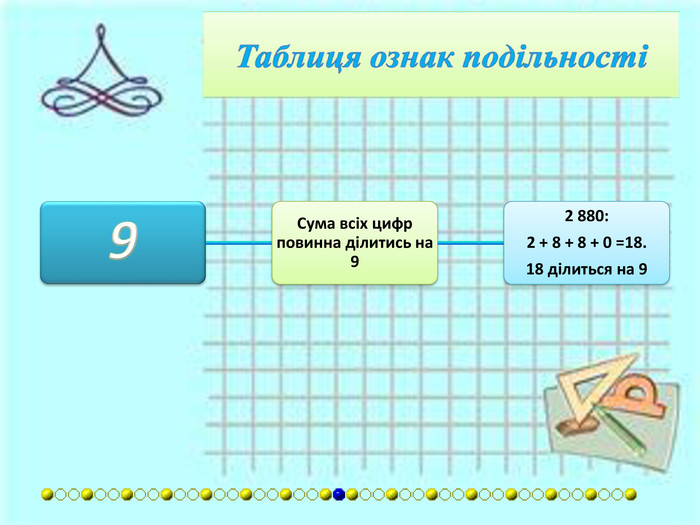
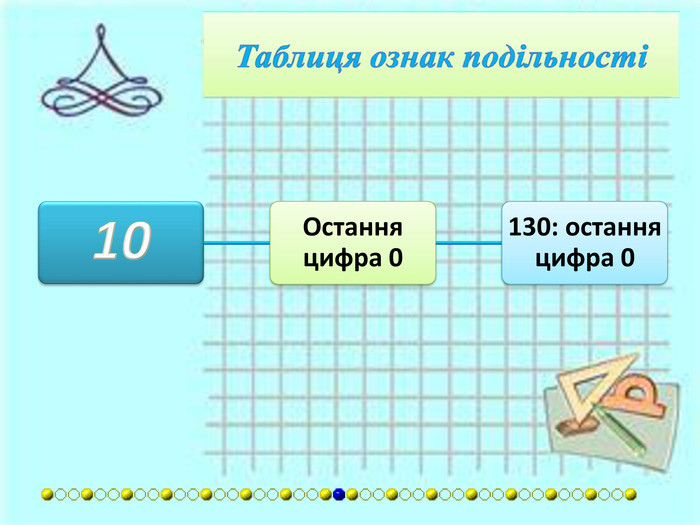
{7 DF18680-E054-41 AD-8 BC1-D1 AEF772440 D}Дільник. Умова подільностіПриклади8 Якщо число, утворене останніми трьома цифрами, ділиться на 8.5 128: 128 ділиться на 8. Якщо число сотень є парне, то число, утворене двома останніми цифрами повинне ділитись на 8.624: 6 - парне, 24 ділиться на 8. Якщо число сотень є непарним, то до числа, утворенного двома останніми цифрами, потрібно додати 4. Таке число повинне ділитись на 8.352: 52+4 = 56. 56 ділиться на 8.9 Сума всіх цифр повинна ділитись на 9.2,880: 2 + 8 + 8 + 0 = =18. 18 ділиться на 9.10 Остання цифра 0.130: остання цифра 0.11 Число розбивається на блоки по дві цифри, починаючи з кінця. Сума блоків повинна ділитись на 11.627: 6 + 27 = 33. 33 ділиться на 11. Якщо різниця між числом без останньої цифри і останньою цифрою ділиться на 11.627: 62 - 7 = 55. 55 ділиться на 11. Якщо сума цифр, що стоять на парних місцях відрізняється від суми цифр, що стоять на непарних місцях, починаючи з кінця, на число, що кратне 11.182 919: (9 + 9 + 8) – -(1 + 2 + 1) = 22.12 Якщо число ділиться на 3 і на 4.324: воно ділиться і на 3, і на 4. Число без останньої цифри множать на два і віднімають останню цифру. Таке число повинне ділитись на 12.324: (32x2) − 4 = 60. 60 ділиться на 12.

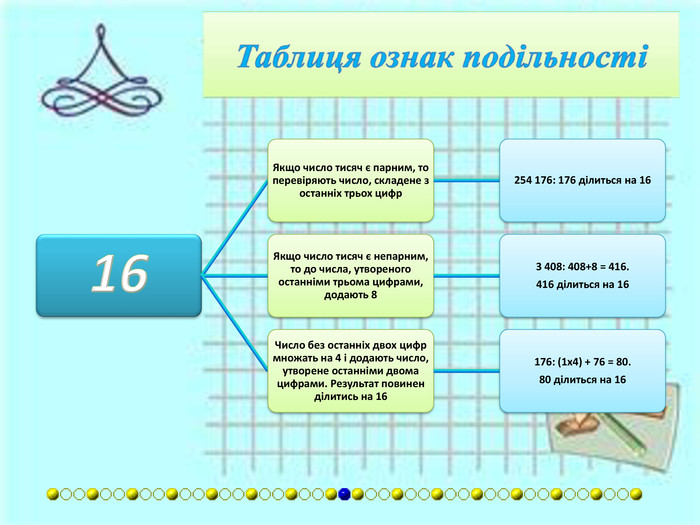
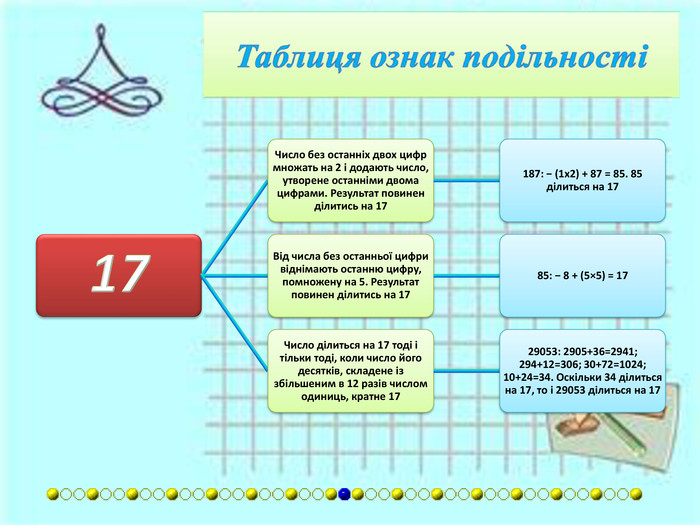
{7 DF18680-E054-41 AD-8 BC1-D1 AEF772440 D}Дільник. Умова подільностіПриклади13 Число ділиться на блоки по три цифри, починаючи з кінця. Сумуються блоки, що стоять на парних і непарних місцях. Різниця цих сум повинна ділитись на 13.2 911 272: 911 - (2 + +272) = 637. 637 ділиться на 13. До числа без останньої цифри додають останню цифру, помножену на 4. Утворене число повинне ділитись на 13.338: 33 + (8×4) = 65. 65 ділиться на 13. Від числа без останньої цифри віднімають останню цифру, помножену на 9. Утворене число повинне ділитись на 13.637: 63 − (7×9) = 0. 0 ділиться на 13.14 Якщо число ділиться на 2 і на 7.224: воно ділиться на і на 2, і на 7. Число без останніх двох цифр множать на 2. До результату додають число, утворене двома останніми двома цифрами. Сума повинна ділитись на 14.364: (3x2) + 64 = 70.15 Якщо число ділиться на 3 і на 5.390: число ділиться на 3 і на 5.16 Якщо число тисяч є парним, то перевіряють число, складене з останніх трьох цифр.254 176: 176 ділиться на 16. Якщо число тисяч є непарним, то до числа, утвореного останніми трьома цифрами, додають 8.3 408: 408+8 = 416. 416 ділиться на 16. Число без останніх двох цифр множать на 4 і додають число, утворене останніми двома цифрами. Результат повинен ділитись на 16.176: (1x4) + 76 = 80. 80 ділиться на 16.17 Число без останніх двох цифр множать на 2 і додають число, утворене останніми двома цифрами. Результат повинен ділитись на 17.187: − (1x2) + 87 = 85. 85 ділиться на 17. Від числа без останньої цифри віднімають останню цифру, помножену на 5. Результат повинен ділитись на 17.85: − 8 + (5×5) = 17. Число ділиться на 17 тоді і тільки тоді, коли число його десятків, складене із збільшеним в 12 разів числом одиниць, кратне 17.29053: 2905+36=2941; 294+12=306; 30+72=102; 10+24=34. Оскільки 34 ділиться на 17, то і 29053 ділиться на 17.

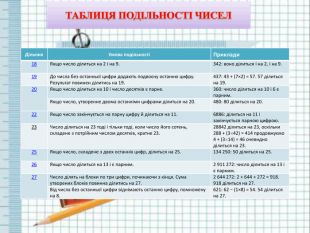
{7 DF18680-E054-41 AD-8 BC1-D1 AEF772440 D}Дільник. Умова подільностіПриклади18 Якщо число ділиться на 2 і на 9.342: воно ділиться і на 2, і на 9.19 До числа без останньої цифри додають подвоєну останню цифру. Результат повинен ділитись на 19.437: 43 + (7×2) = 57. 57 ділиться на 19.20 Якщо число ділиться на 10 і число десятків є парне.360: число ділиться на 10 і 6 є парним. Якщо число, утворенне двома останніми цифрами ділиться на 20.480: 80 ділиться на 20.22 Якщо число закінчується на парну цифру й ділиться на 11.6886: ділиться на 11 і закінчується парною цифрою.23 Число ділиться на 23 тоді і тільки тоді, коли число його сотень, складене з потрійним числом десятків, кратне 23.28842 ділиться на 23, оскільки 288 + (342) = 414 продовжуємо 4 + (314) = 46 очевидно ділиться на 23.25 Якщо число, складене з двох останніх цифр, ділиться на 25.134 250: 50 ділиться на 25.26 Якщо число ділиться на 13 і є парним.2 911 272: число ділиться на 13 і є парним.27 Число ділять на блоки по три цифри, починаючи з кінця. Сума утворених блоків повинна ділитись на 27.2 644 272: 2 + 644 + 272 = 918. 918 ділиться на 27. Від числа без останньої цифри віднімають останню цифру, помножену на 8.621: 62 − (1×8) = 54. 54 ділиться на 27.

{7 DF18680-E054-41 AD-8 BC1-D1 AEF772440 D}Дільник. Умова подільностіПриклади32 Якщо число десятків тисяч є парним, то перевіряють на подільність число, утворене останніми чотирма цифрами.41 312: 1312 ділиться на 32. Якщо число десятків тисяч є непарним, то до числа, утвореного останніми чотирма цифрами, додають 16.254 176: 4176+16 = 4192. 4192 ділиться на 32. Число без останніх двох цифр множать на 4 і до результату додають останні дві цифри. Суму перевіряють на подільність на 32.1 312: (13×4) + 12 = 64. 64 ділиться на 32.33 Якщо число ділиться на 11 і на 3.1 003 002: число ділиться на 11 і на 3. Число ділять на блоки по дві цифри, починаючи з кінця. Утворені блоками числа сумують. Результат повинен ділитись на 33.627: 6 + 27 = 33.37 Число ділять на блоки по три цифри, починаючи з кінця. Число, утворені блоками сумують. Сума повинна ділитись на 37.2 651 272: 2 + 651 + 272 = 925. 925 ділиться на 37. Від числа без останньої цифри віднімають останню цифру, помножену на 11. Результат повинен ділитися на 37.925: 92 − (5×11) = 37.49 До числа без останньої цифри додають останню цифру, помножену на 5. Таке число повинне ділитись на 49.1 127: 112 + (7×5) = 147. 147 ділиться на 49.99 Розіб'ємо число на групи по 2 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп, вважаючи їх двозначними числами. Ця сума ділиться на 99 тоді і тільки тоді, коли саме число ділиться на 99.53064 ділиться на 99, оскільки 5+30+64=99 ділиться на 99.101 Розіб'ємо число на групи по 2 цифри справа наліво (у найлівішій групі може бути одна цифра) і знайдемо суму цих груп із змінними знаками, вважаючи їх двозначними числами. Ця сума ділиться на 101 тоді і тільки тоді, коли саме число ділиться на 101.590547 ділиться на 101, оскільки 59-05+47=101 ділиться на 101.

Подивитися на останню цифру числа. Остання цифра 0?Остання цифра 5?Остання цифра парна?Число ділиться на 2, на 5 і на 10 Число ділиться на 5 Число ділиться на 2 Число не ділиться ні на 2, ні на 5, ні на 10 АЛГОРИТМ ВИЗНАЧЕННЯ ПОДІЛЬНОСТІ НА 10, НА 2 І НА 5 ТАКТАКТАКНІНІНІ

Знайти суму цифр числа. Сума цифр числа ділиться на 9?Сума цифр числа ділиться на 3?Число ділиться на 3 і на 9 Число ділиться на 3, але не ділиться на 9 Число не ділиться ні на 3, ні на 9 АЛГОРИТМ ВИЗНАЧЕННЯ ПОДІЛЬНОСТІ НА 3 І НА 9 ТАКТАКНІНІ

КЛАСИФІКАЦІЯ ОЗНАК ПОДІЛЬНОСТІ

ЗАДАЧІ НА ЗАСТОСУВАННЯ ОЗНАК ПОДІЛЬНОСТІ Яке найменше число треба задумати, щоб після збільшення його на 7 або на 19 результат ділився відповідно на 7 або на 19, після зменшення на 17 результат розділився б на 17, а після ділення його на 11 і результат розділився б на 11?Очевидно, що задумане число повинне ділитися на 7, 19, 17 і двічі на 11. Найменшим таким числом є 19∙17∙11∙11∙7= 273 581. Легко перевірити, що його подільність на свої множники зберігається як при збільшенні на 7 або 19, так і при зменшенні на 17.

Число ― монарх, що зводиться на трони, На книги й вежі міст являти чудо й суд. І замкнуто міста, і замкнуто закони, І в знаках чисел входить абсолют.

В своїй роботі я навів доведення основних ознак подільності натуральних чисел, приклади їх застосування для встановлення подільності одного числа на інше, а також при розв’язуванні задач підвищеної складності на доведення подільності чисел, або ж на знаходження остачі від ділення чисел, яку звичним способом знайти практично неможливо. ВИСНОВКИ

А також зробив систематизацію ознак подільності натуральних чисел у вигляді таблиці подільності, побудував алгоритм застосування деяких ознак подільності, класифікував ознаки за спільним принципом. ВИСНОВКИ

Матеріали моєї роботи можна використати на уроках математики при вивченні теми «Подільність натуральних чисел», а також для проведення факультативних та гурткових занять з математики та при підготовці до математичних олімпіад. ПРАКТИЧНЕ ВИКОРИСТАННЯ