Презентація "Паралельне перенесення"
Про матеріал
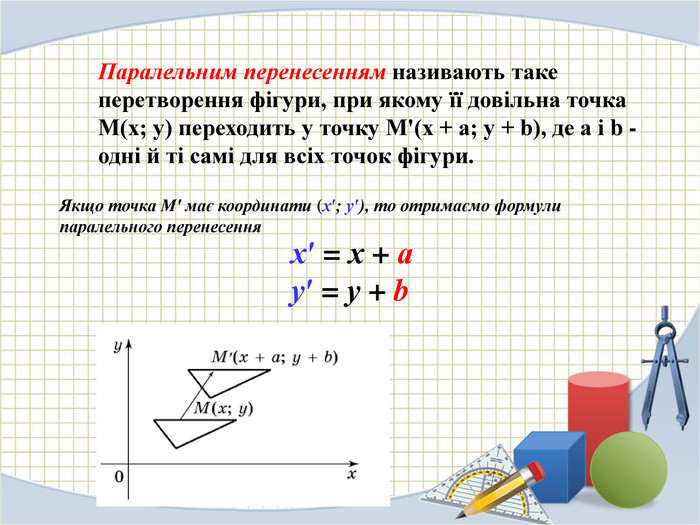
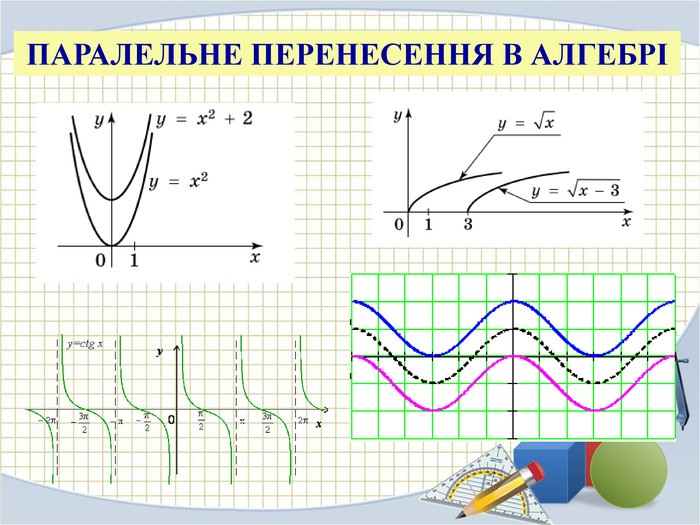
У презентації розглядаються основні властивості паралельного перенесення фугур та розв'язки задач, пов'язаних з даною темою Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
























-

Чуб Тамара Михайлівна
14.04.2025 в 22:26
Дякую. Використаю у своїй роботі
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кухтін Юлія Олександрівна
14.04.2025 в 20:21
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Веремейчик Наталія Миколаївна
08.04.2025 в 08:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Романчук Ірина Василівна
10.03.2025 в 17:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Лоцман Наталья
04.04.2024 в 22:39
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Вигоднер Діана Ісаківна
02.04.2024 в 14:48
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука