Паралельність прямих і площин

ознайомити учнів з поняттям

паралельного проектування та його властивостями; навчити учнів

застосовувати знання з теми для

розв’язування задач; показати широке коло застосування

властивостей паралельного

проектування у навколишньому світі

математик, фізіолог, фізик

АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Вправа на відповідність

                      №1                  ЗГАДАЙТЕ, ЗНАДОБИТЬСЯ!

1.            Стереометрія – це розділ геометрії, в якому вивчаються…

2.            Пряма і площина називаються паралельними, якщо вони… 3. Основні фігури стереометрії…

4.    Основна властивість пропорції …

5.    Прямі паралельні, якщо вони…

6.    Вписаний кут, що опирається на діаметр… 7. Прямі мимобіжні, якщо вони…

8. Правильний трикутник - це…

ВІДПОВІДЬ

А) точка, пряма, площина

Б) добуток середніх членів дорівнює добутку крайніх

В)  не перетинаються і не лежать в одній площині

Г) рівносторонній

Д) прямий

Е) не перетинаються

Є) не перетинаються і лежать в одній площині

Ж) властивості фігур у просторі

Ми неодноразово зустрічаємося з паралельним

проектуванням у житті. Наприклад, наша тінь у сонячний день на рівному асфальті є нашою

паралельною проекцією, оскільки сонячні промені наближено можна

вважати паралельними зважаючи на велику

віддаленість Сонця від

Землі

У дитинстві ми всі любили грати з тінями,

показуючи за

допомогою рук

кілька класичних фігур - собачку, зайчика, пташку.

Людські руки здатні

створити на

освітленій стіні дивовижний

світ, причому неймовірно реальний.

Театри тіней створюють дивовижні силуетні образи за допомогою власного тіла

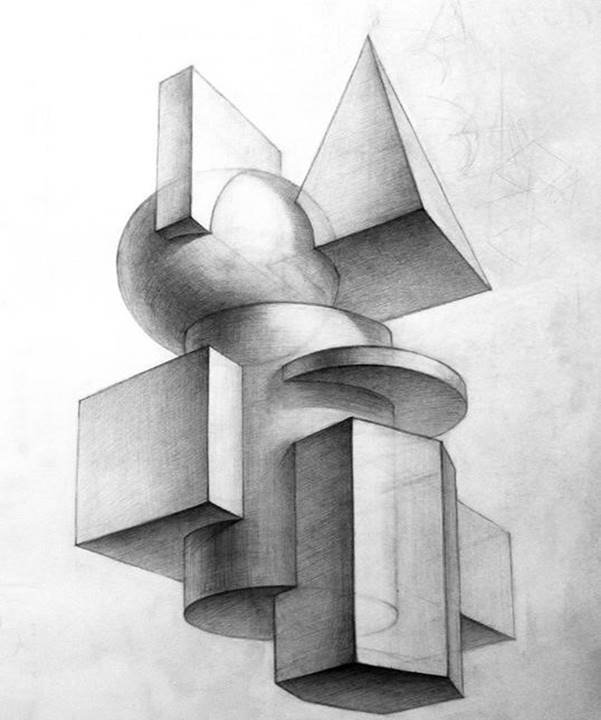
Зобразити тривимірний об’єкт

на плоскому

кресленні з

абсолютною точністю неможливо. Однак за допомогою плоского рисунка можна

одержати досить чітке уявлення про окремі властивості плоских фігур.

Щоб плоскі рисунки давали

якомога чіткіше уявлення про

властивості тієї чи іншої просторової фігури, необхідно знати правила зображення

просторових фігур на площині

Ними користуються

Художники, що малюють тінню…

Вони порушують усі можливі закони мистецтва. Адже «пишуть»

двовимірні картини за допомогою тривимірних скульптур, і їх улюблений «матеріал» - це тінь ...

Колекції створені за допомогою ламп та

розкладеного непотрібу.

Їхні роботи спроба

створити досконалу красу з

відвертого сміття

Наприклад,

голандець Дієт Вігман

Натюрморт створено за допомогою

різнокольорових зім’ятих

пластикових пляшок,

підсвічених лампою

Скульптура, складена з

монет, утворює на стіні тінь титана

Атланта, який, послизнувшись, насилу утримує

Землю на вазі

Гілки у горщику

утворюють римський профіль

Венера у вогні

Тіньовий танець

«Давид після обіду», 1983

Матеріал — деформовані кухонні приладдя Азербайджанський художник Рашад

Алакбаров, який працює з… тінню

Пейзаж створено за допомогою різнокольорових дитячих літачків, підсвічених лампою

Незвичайні скульптури, які при підсвічуванні відкидають химерні тіні

Не менш оригінальні проекти пропонує грецький художник Теодосій Ауреа (Teodosio

Sectio Aurea)

Неповторна  «Акіна» - тінь японскої сакури Створює работи з тінями і 3D композиціями

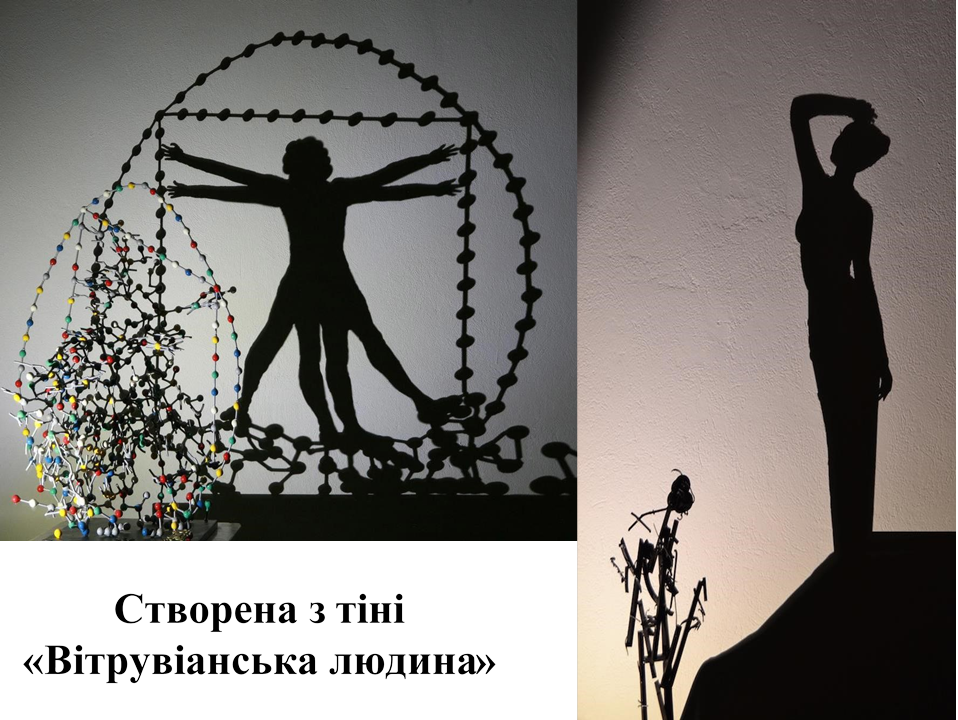
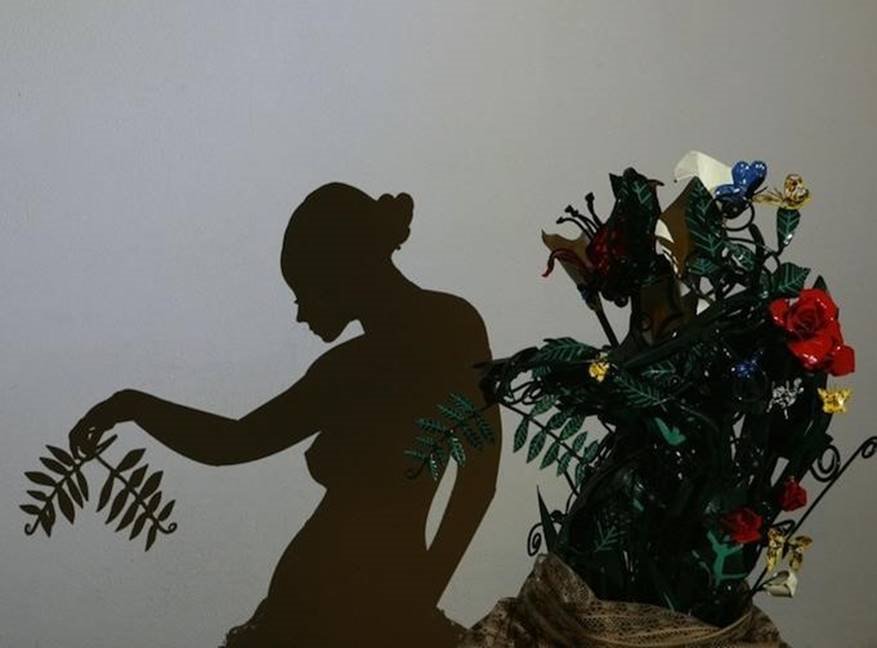Муза

Слово проекція виникло від

латинського projection кидання вперед, вдалину.

Паралельне проектування

Ми вивчаємо стереометрію –

геометрію у просторі. Як завжди, нам необхідно вміти

зображувати

геометричні фігури,

причому всі креслення ми

і досі виконуємо на

площині (на сторінці зошита, на дошці тощо).

Яким чином  просторову фігуру

(наприклад , куб) можна

«вкласти» до площини?

Для розв'язання цієї задачі

приймається метод

паралельного проектування

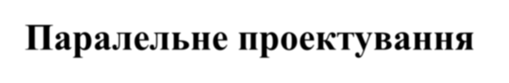Паралельне проектування

Паралельне проектування

— це зображення довільної геометричної фігури на площині, при якому всі

точки фігури переносяться на площину за прямими,

паралельними заданій, яку називають напрямком проектування.

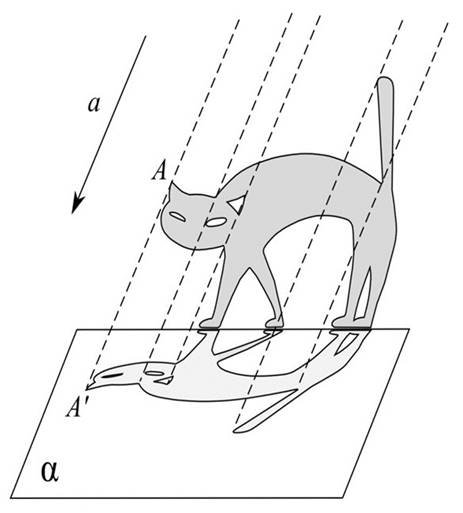
Пряма a задає напрямок проектування, α — площина проекції.

З'ясуємо  суть метода паралельного проектування  на прикладі найпростішої  геометричної фігури – точки.

Таким чином, у нас є геометрична фігура у просторі  – точка А.

А

Оберемо у просторі довільну площину  (площину проекцій) та довільну  пряму a∩^(a задає напрямок паралельного

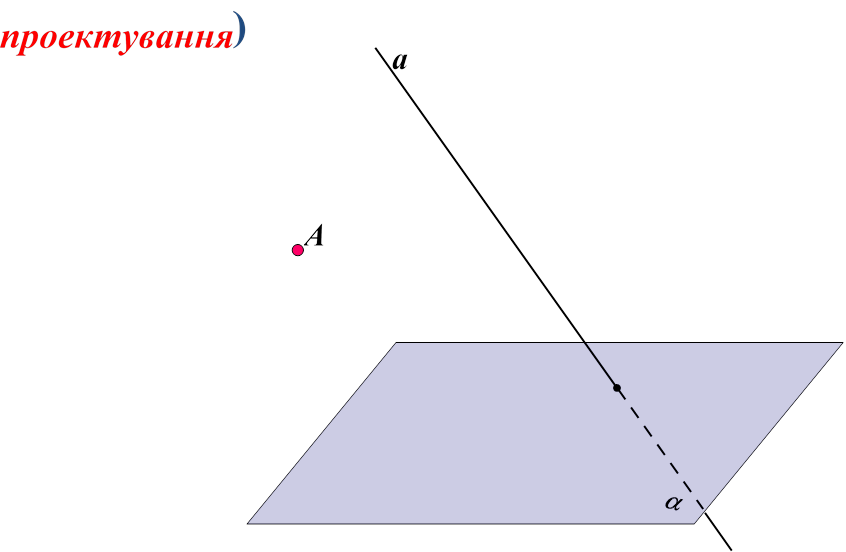
Проведемо через точку А пряму, паралельну до прямої а.

Точка А′ перетину цієї прямої з площиною  є проекція точки А на площину . Точка А - оригінал, а точка А′ – зображення.

Якщо А, то А′ співпадає з А.

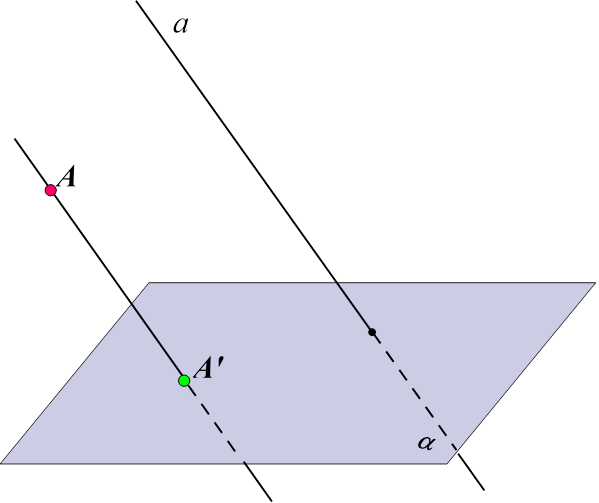
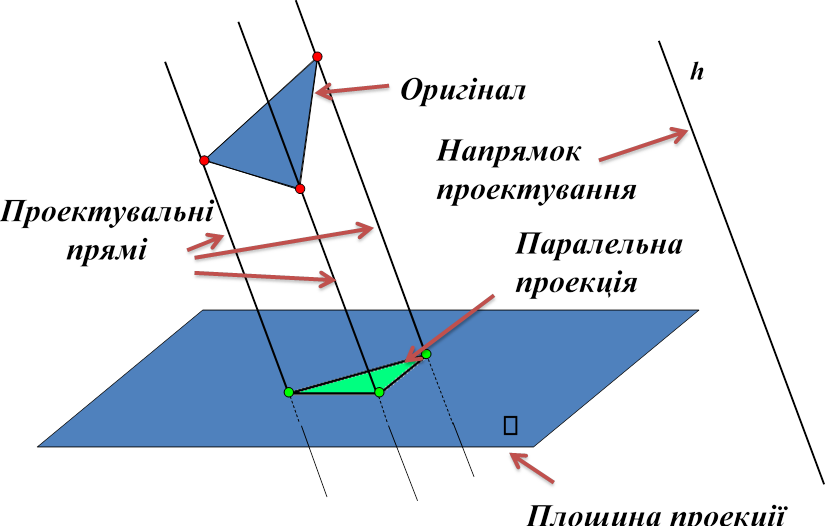
Якщо розглянемо будь-яку геометричну фігуру як множину точок, то можна побудувати в заданій площині проекцію даної фігури.

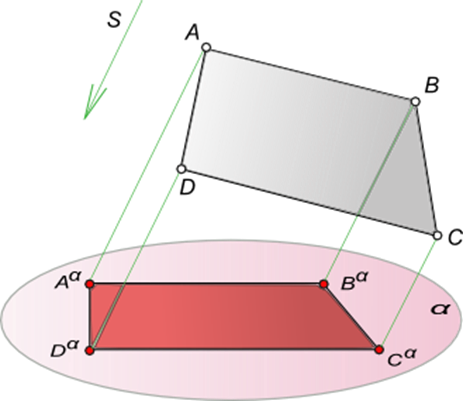
Таким чином можна отримати зображення (або

«проекцію») будь-якої плоскої фігури або просторового

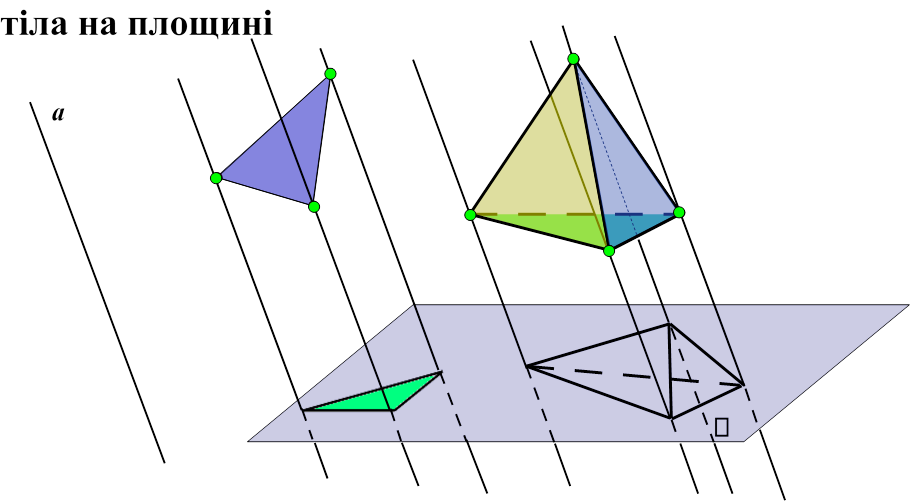
Побудуємо зображення куба (куб «вкладемо» на площину)

Зауваження 1. При паралельному проектуванні не обирають напрямок проектування паралельно до

площини проекції (самостійно поясніть чому).

а

А

Зауваження 2. При паралельному проектуванні плоских фігур не обирають напрямок проектування паралельно до площини,

в якій лежить ця плоска фігура, оскільки проекція, яка при цьому отримується, не відображає властивості даної плоскої

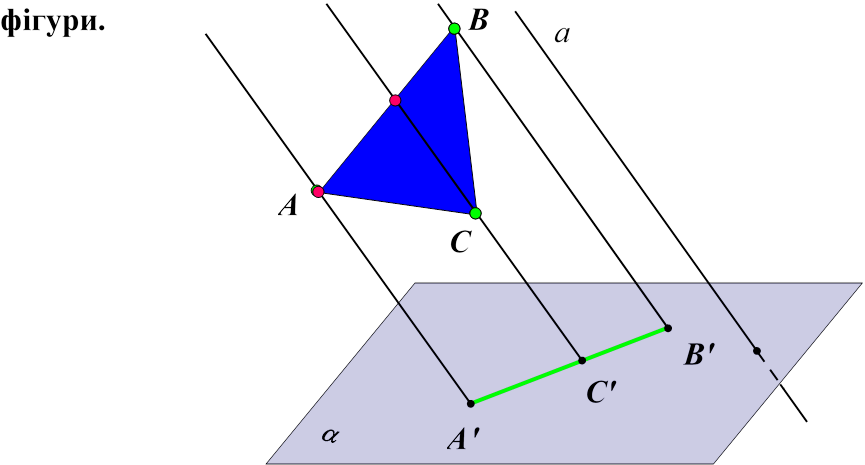
Таку проекцію називають ^{виродженою}.

Зауваження 3. Якщо напрямок паралельного проектування перпендикулярний до площини

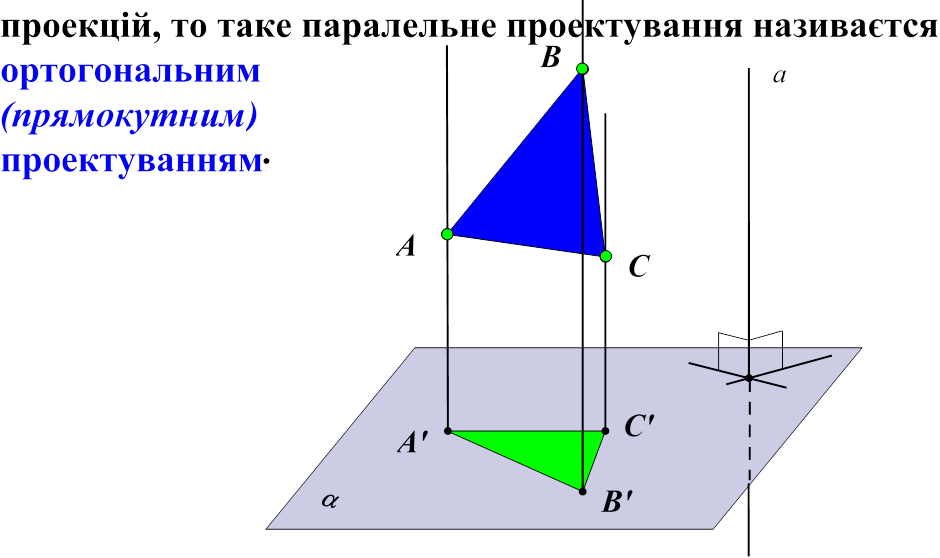
Зауваження 4. Якщо площина проекцій та площина, в якій лежить дана фігура, паралельні (||(АВС)), то

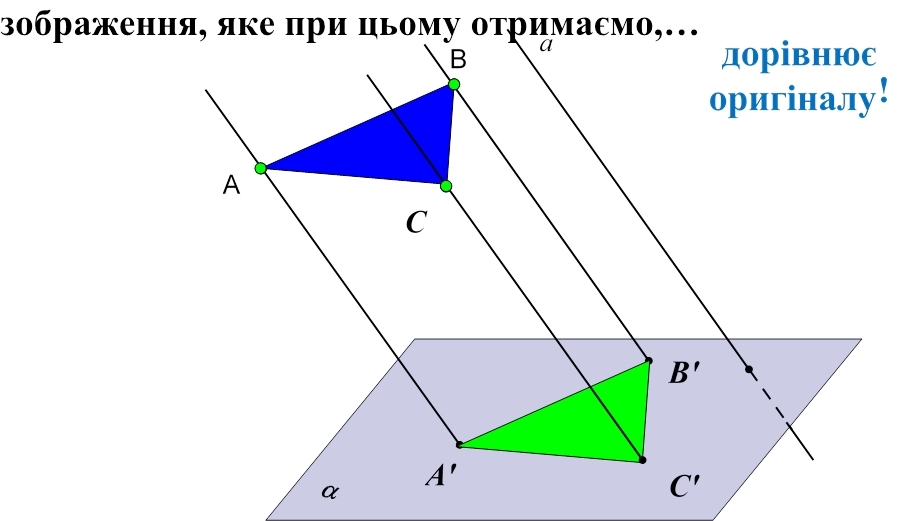
Властивості паралельного проектування:

1)    відрізки зображаються відрізками;

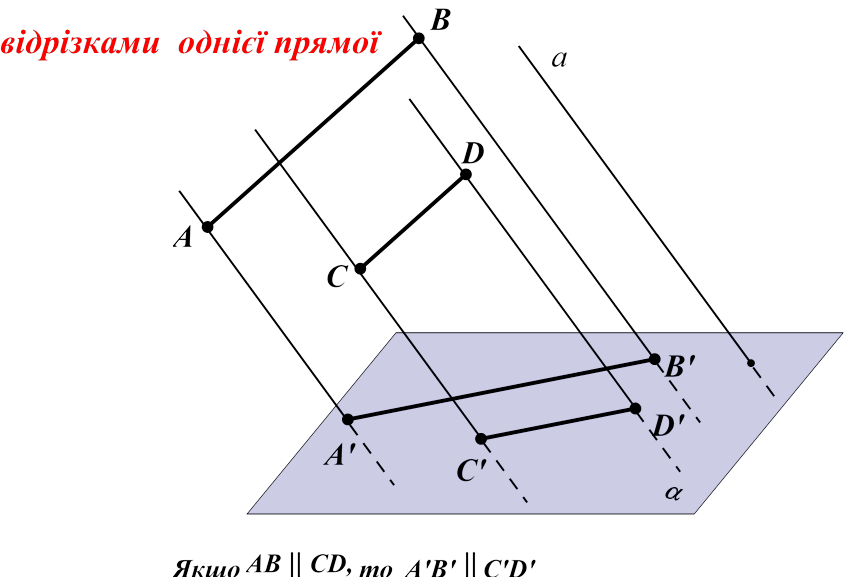
2)    паралельні відрізки – паралельними відрізками або

1) Відрізки зображаються відрізками

                                                        Оригінал                    Зображення

Паралельні відрізки зображаються паралельними відрізками або відрізками однієї прямої

                                                                     B1          C1

                                        A                          D                  A1                         D1

                                                             Оригінал                   Зображення

Властивості паралельного проектування:

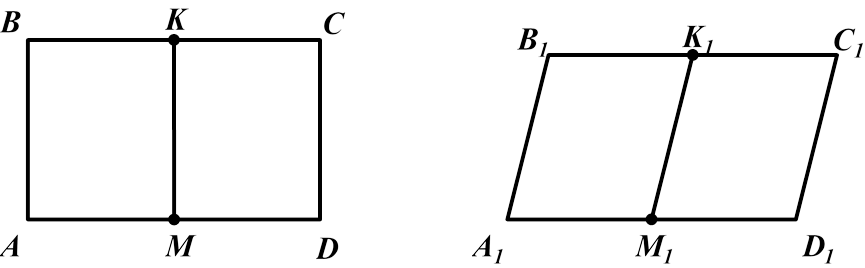
3) відношення довжин відрізків, які лежать на паралельних або на одній прямій, зберігається;

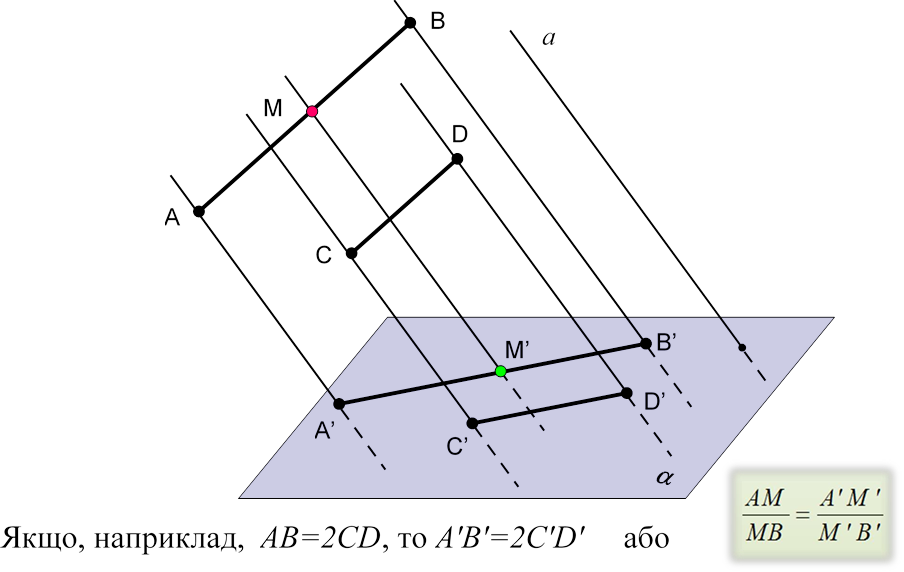
3. Відношення довжин паралельних відрізків і відрізків однієї прямої зберігаються

                                                       Оригінал                              Зображення

               B                      K                   C

                                                                                                                                                                                         B₁                                                                                                               K1                  C₁

                                                                                                                                                                               A1       M        D

               A          M                              D                       1             1

                                                  AB : BC = 1 : 2              A₁B₁ : B₁C₁ = 1 : 2

                                                  CD : AD = 1 : 2             C1D1 : A1D1 = 1 : 2

BK : KC = B₁K₁ : K₁C₁ AM : MD = A₁M₁ : M₁D₁

Властивості паралельного проектування:

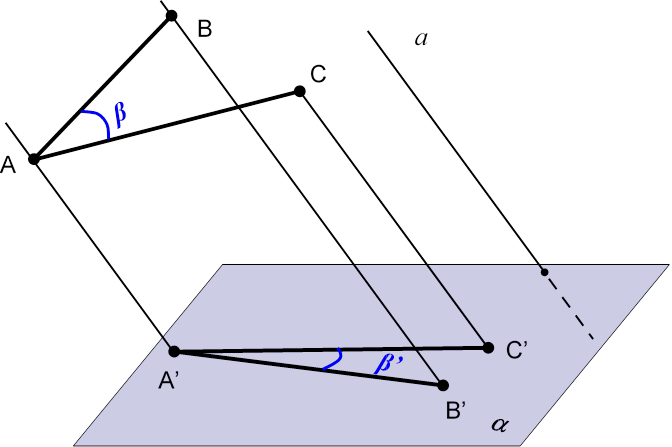
4) Лінійні розміри плоских фігур (довжини відрізків, величини кутів) НЕ ЗБЕРІГАЮТЬСЯ (виключення:

якщо площина проекцій та площина, в якій лежить дана фігура паралельні).

ЗБЕРІГАЮТЬСЯ

НЕ ЗБЕРІГАЮТЬСЯ

1)     Належність фігури до свого класу фігур (точку зображають точкою, пряму – прямою, відрізок – відрізком, трикутник – трикутником, тощо); 2)     Належність точок прямій; 3)     Порядок розміщення точок на прямій (внутрішню точку відрізка зображають внутрішньою точкою відрізка); 4)     Паралельність прямих; 5)     Рівність (пропорційність) відрізків, що лежать на паралельних прямих або на одній прямій

1)     Довжина відрізка; 2)     Міра кута (зокрема, прямий кут зображають довільним кутом); 3)     Перпендикулярність прямих; 4)     Рівність (пропорційність) кутів; 5)     Рівність (пропорційність)  відрізків, які лежать на прямих, що перетинаються.

Властивості фігур під час паралельного проектування

(№2) Вправа 1 (тест)

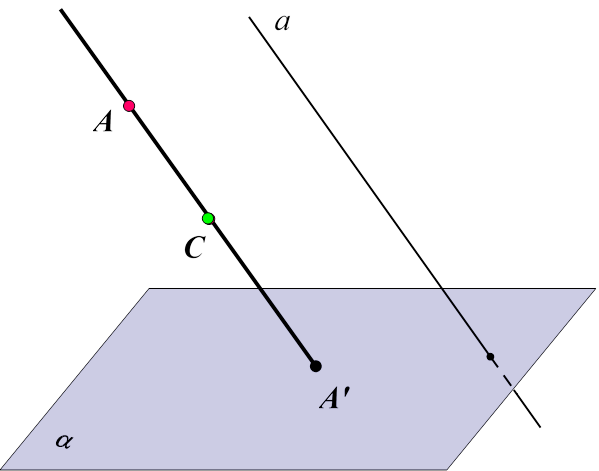
В якому випадку паралельною

проекцією прямої буде точка?

А) Якщо пряма паралельна напрямку паралельного проектування

Б) Якщо пряма паралельна проектуючій площині

В) Якщо пряма перетинає площину проекцій

Г)  Якщо пряма перетинає пряму, що задає напрямок паралельного проектування

Відповідь: Якщо пряма паралельна напрямку проектування

Вправа 2 (тест) 

Скільки точок можна отримати при паралельному проектуванні

трьох різних точок простору?

А) Три

Б) Одну

В) Три, або дві, або одну

Г) Дві

Відповідь: три, або дві, або одну І випадок: три

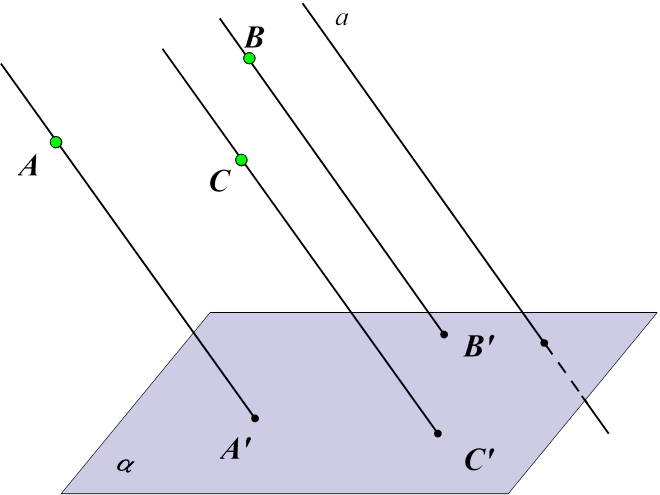
Відповідь: три, або дві, або одну ІІ випадок: дві (коли дві з трьох точок лежать на одній прямій, яка паралельна до напрямку проектування

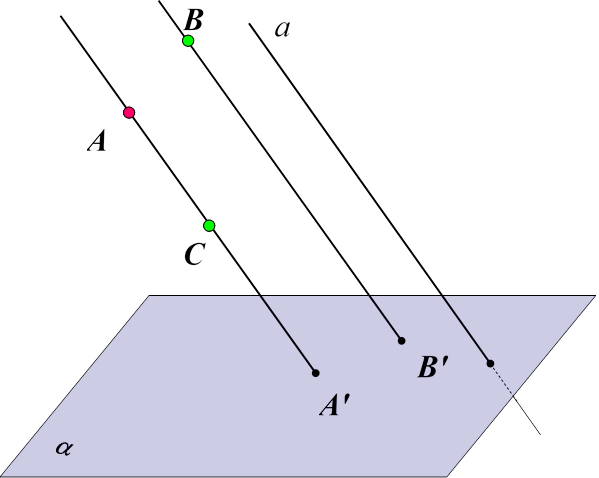
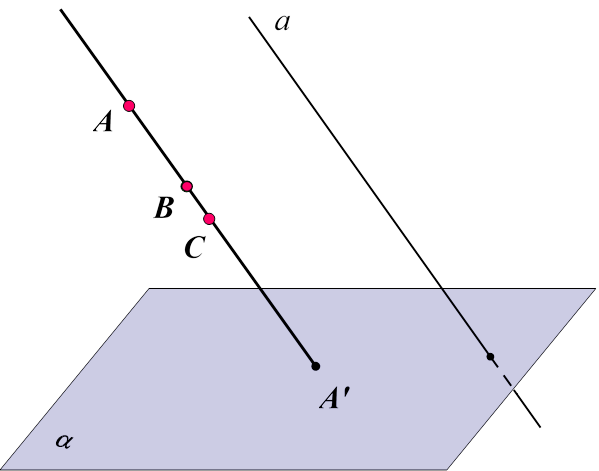
Відповідь: три, або дві, або одну ІІІ випадок: одну (коли три точки лежать на одній прямій, паралельній напрямку проектування)

Вправа 3 (тест)

Які фігури можуть бути паралельними проекціями прямих, що перетинаються?

А) дві прямі, що перетинаються

Б) одна пряма

В) дві паралельні прямі

Г) дві прямі, що перетинаються, або одна пряма

Відповідь: дві прямі, що перетинаються, або одна пряма

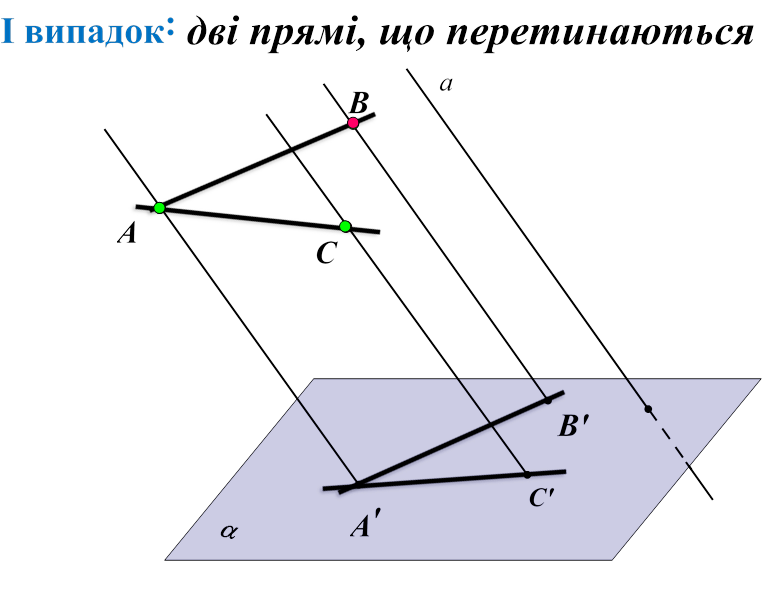
Відповідь: дві прямі, що перетинаються

ІІ випадок: одна (коли прямі, що перетинаються, (прообрази),

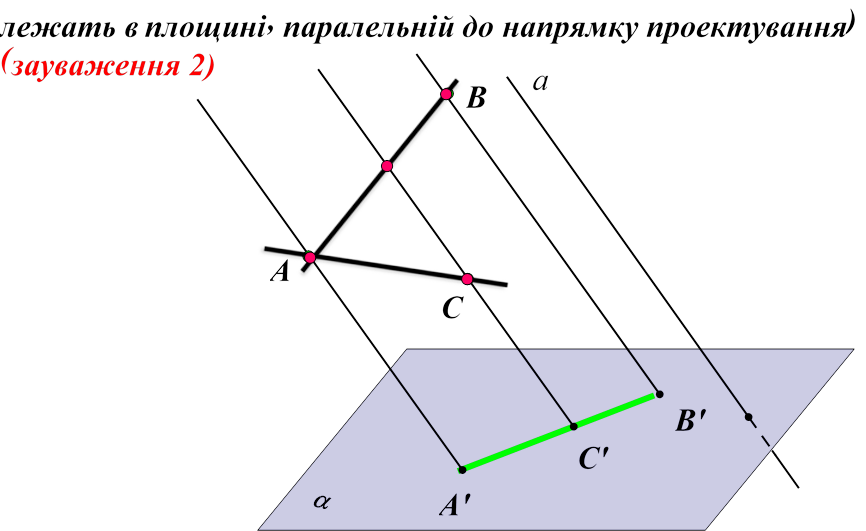
Вправа 4 (тест)

Яка фігура не може бути паралельною проекцією трапеції?

Вправа 5 (тест)

Яка фігура не може бути паралельною проекцією правильного трикутника, у якого

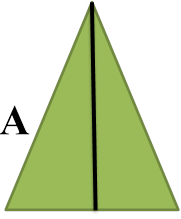
Вправа 6 (тест)

Яка фігура не може бути паралельною проекцією ромба?

В

Вправа№7 (тест)

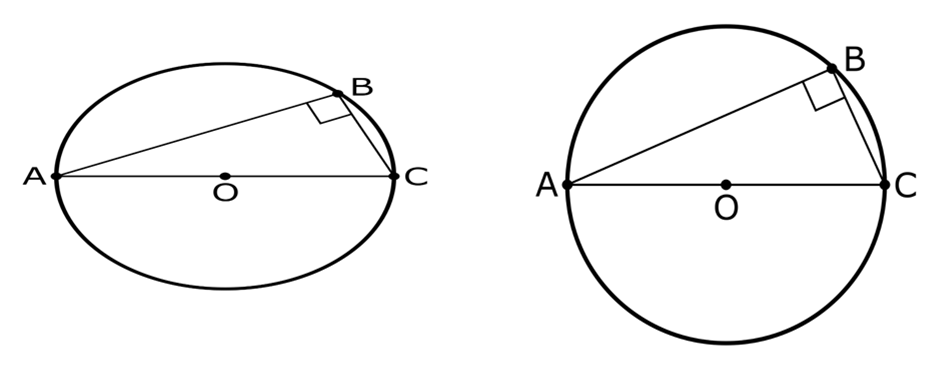
Зображенням якого трикутника є ∆АВС, якщо точка В лежить на еліпсі, а АС – діаметр цього еліпса

А) ∆АВС – зображення гострокутного ∆, вписаного в коло

Б) ∆АВС – зображення тупокутного ∆, вписаного в коло

В) ∆АВС – зображення прямокутного ∆, вписаного в коло

Г) ∆АВС – зображення гострокутного ∆, описаного навколо кола

Відповідь: ∆АВС – зображення прямокутного трикутника, вписаного в

коло

(№3) Проблемне питання

Чи перетинаються прямі АВ і СD, зображені на малюнку,

якщо А₁ B₁ іC₁ D₁ – їхні проекції на площину ?

Розв’язання:

Припустимо, що прямі АВ і СD перетинаються.

Тоді проекція точки їх перетину повинна лежати на проекціях прямих .

А оскільки проекції А₁ B₁ іC₁ D₁ паралельні (не мають спільних точок), то прямі АВ і СD не перетинаються.

Отже, прямі АВ і СD – мимобіжні, і їх паралельною проекцією є паралельні прямі.

(№3) Проблемне питання

Які ще фігури можуть бути паралельними проекціями мимобіжних прямих?

Відповідь: прямі, що перетинаються; пряма і точка

Як повинні розташовуватись мимобіжні прямі, щоб їх проекцією на площину були пряма і точка?

Відповідь: Одна з них повинна бути паралельною напрямку проектування (№4) Пошуковий практикум

Паралельною проекцією точок А,

В і С (точка С лежить між А і В) на ^B площину  є точки А₁, B₁ іC₁ . Знайдіть А₁B₁ і А₁C₁ , якщо

АВ = 20 см, ВС = 8 см, а B₁C₁ = 2 см Розв’язання:

За 3-тьою властивістю паралельного проектування (про

АВВС  АB¹₁BC¹₁ ^.     _Тобто 208 = А12B1, пропорційні відрізки) =

                                    А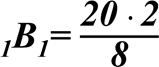 = 5 (см)

Тоді А1C1 = А1B1 - B1C1 = 5 – 2 = 3 (см)                                         Відповідь: 5 см; 3 см

Пошуковий практикум (додатково)

Чи може паралельною проекцією паралелограма бути чотирикутник зі сторонами 6 см, 8 см, 6 см,

9 см ?

Розв’язання:

Ні, оскільки при паралельному проектуванні паралельність відрізків зберігається.

Тому паралельною проекцією паралелограма може бути або паралелограм, або ромб, або прямокутник, або квадрат.

А отже протилежні сторони  паралельної проекції паралелограма паралельні і рівні.

Пошуковий практикум (додатково)

AN бісектриса,

AM – медіана,

AH – висота ∆ АВС.

Чи буде паралельною проекцією відрізків AN, AM, AH бісектриса, медіана, висота ∆А1В1С1 ?

Відповідь обгрунтуйте.

Розв’язання:

Медіана A₁М₁ ∆А₁В₁С₁ буде паралельною проекцією медіани AN ∆АВС (зберігається відношення відрізків (середина відрізка переходить в середину проекції цього відрізка).

Бісектриса A₁N₁ і висота A₁H₁ ∆А₁В₁С₁ не будуть паралельними проекціямибісектриси AN і висоти АН

∆ АВС (кути не зберігаються)

(№5) Вправа «Вірю – не вірю»

( за кожну вірну відповідь – 1 бал)

1)                  При паралельному проектуванні зберігаються величини кутів

2)                  При паралельному проектуванні зберігаються довжини відрізків

3)                  Паралельна проекція кута може бути більше (менше) самого кута

4)                  Паралельна проекція відрізка може бути більше (менше) самого відрізка

(№5) Вправа «Вірю – не вірю»

( за кожну вірну відповідь – 1 бал)

5)                  При паралельному проектуванні відрізків можна отримати точки

6)                  Паралельна проекція квадрата може бути трапецією

7)                  Паралельною проекцією двох паралельних прямих можуть бути  прямі, що перетинаються

                                                                               Вправа «Вірю – не вірю»                                         

( за кожну вірну відповідь – 1 бал) 8) Паралельною проекцією трапеції з основами  4 см і 8 см може бути трапеція з основами 2 см і 6 см

9)                   Паралельною проекцією правильного трикутника  з Р =12 см може бути тупокутний трикутник з Р = 21 см

10)        Якщо точка С належить відрізку АВ,

С′ -проекція точки С, А′ - проекція точки  А, В′ - проекція точки В, то точка С′ належить відрізку А′В′

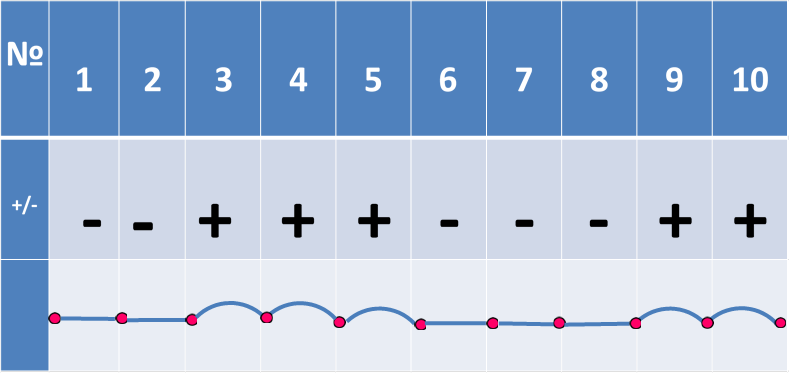
ПЕРЕВІРКА У ПАРАХ

Вправа «Вірю – не вірю»

( за кожну вірну відповідь – 1 бал) максимальна кількість – 10 балів

Рефлексія. На початку уроку була поставлена мета.

Чи досягли її?

Пропоную вам продовжити речення…

•           Сьогодні на уроці я навчився…

•           Сьогодні на уроці я дізнався…

•           Несподіваним відкриттям для мене було…

•           Найбільший мій успіх – це…

•           Уроком я  (не) задоволений…