Презентація "Періодичність функцій. Властивості та графіки тригонометричних функцій".
Про матеріал
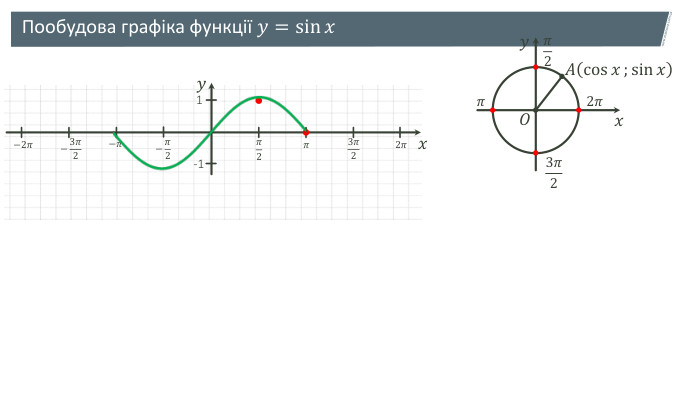
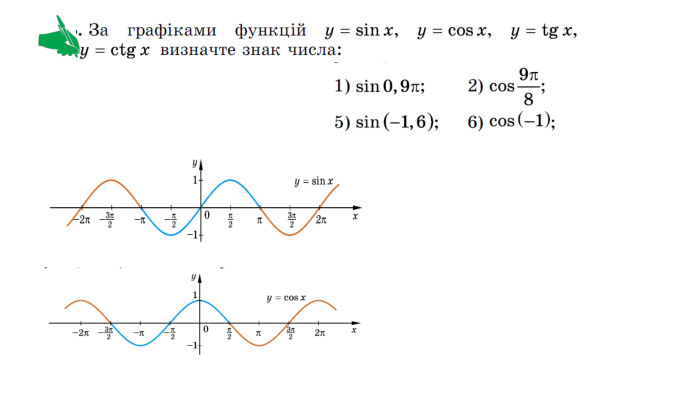
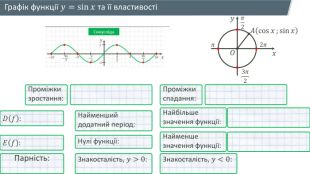
Презентація містить матеріали, які допоможуть при вивченні теми "Періодичність функцій. Властивості та графіки тригонометричних функцій" (дистанційно). Звертається увага на означення періодичної функції, на побудову графіків тригонометричних функцій, як за графіками сформулювати їх властивості. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку