Узагальнена таблиця "Степенева функція"
Степенева функція –
це функція, що визначається рівнянням![]() , де - стале число, причому 0.
, де - стале число, причому 0.
|
№п/п |
Функція |
D(f) |
Парність |
Графік |
Приклад |
|
І |
|||||
|
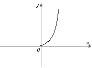
1 |
|
|
парна |
|
|
|
2 |
|
|
непарна |
|
|
|
3 |
|
|
парна |
|
|
|
4 |
|
|
непарна |
|
|
|
ІІ |
|
||||
|
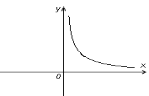
1 |
|
|
ні парна, ні непарна |
|
|
|
2 |
|
|
ні парна, ні непарна |
|
|
|
3 |
|
|
ні парна, ні непарна |
|
|
|
4 |
|
|
ні парна, ні непарна |
|
|
|
5 |
|
|
ні парна, ні непарна |
|
|
|
6 |
|
|
ні парна, ні непарна |
|
|
|
7 |
|
|
ні парна, ні непарна |
|
|
|
8 |
|
|
ні парна, ні непарна |
|
|
|
9 |
|
|
ні парна, ні непарна |
|
|
Зауваження: Степеневу функцію ![]() , де - дробове, найчастіше визначають як таку, що має область визначення
, де - дробове, найчастіше визначають як таку, що має область визначення ![]() >0 (хоча існує і інша точка зору).
>0 (хоча існує і інша точка зору).
Функція![]()
![]() ,де
,де ![]() - нескоротний дріб, m, n N, n 2
- нескоротний дріб, m, n N, n 2
|
№ п/п |
Функція |
D(f) |
Парність |
Графік |
Приклад |
|
1 |
|||||
|
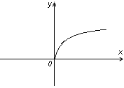
a) |
|
|
ні парна, ні непарна |
|
|
|
б) |
n –непарне, m - непарне |
|
непарна |
|
|
|
в) |
n –непарне, m - парне |
|
парна,
|
|
|
|
2 |
|||||
|
a) |
|
|
ні парна, ні непарна |
|
|
|
б) |
n –непарне, m - непарне |
|
непарна |
|
|
|
в) |
n –непарне, m - парне |
|
парна |
|
|
|
3 |
|||||
|
a) |
|
|
ні парна, ні непарна |
|
|
|
б) |
n –непарне, m - непарне |
|
непарна |
|
|
|
в) |
n –непарне, m - парне |
|
парна |
|
|

про публікацію авторської розробки
Додати розробку