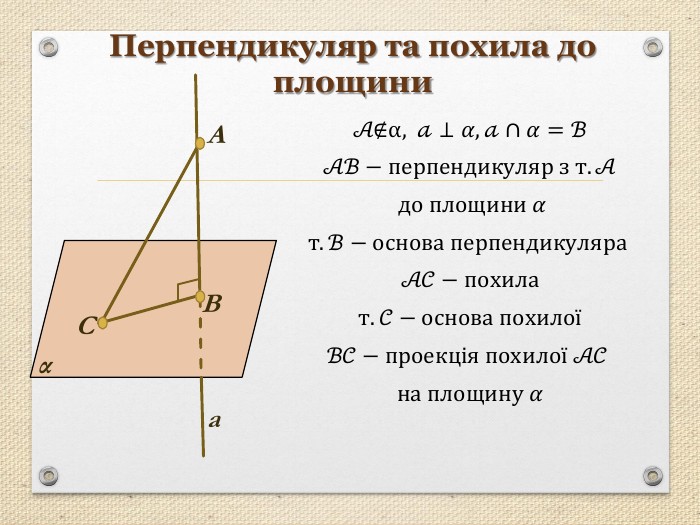
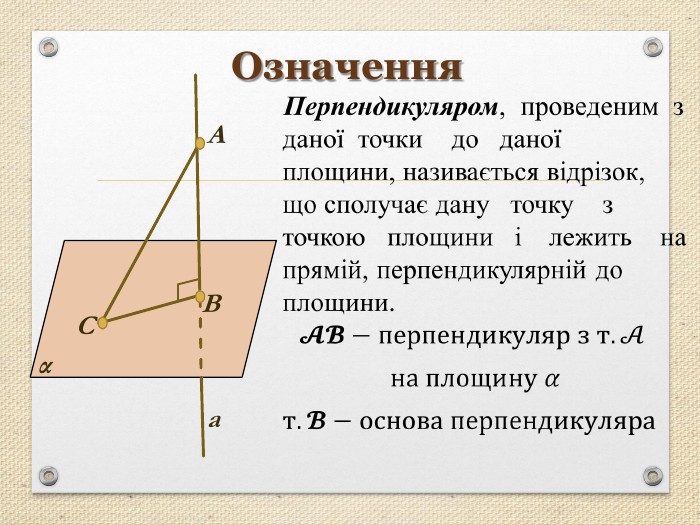
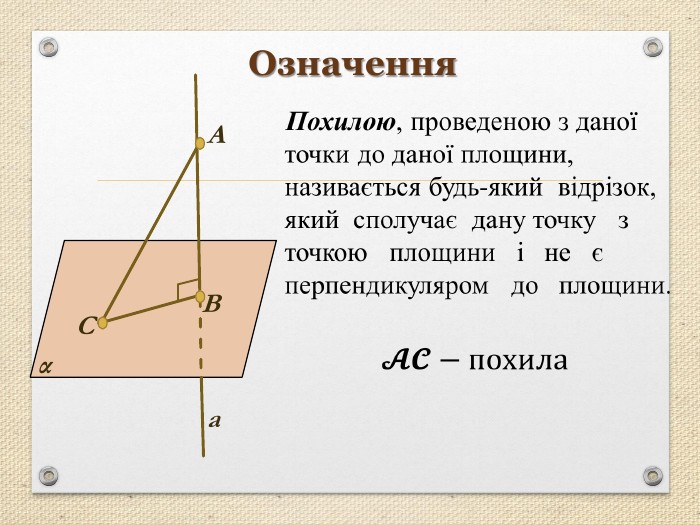
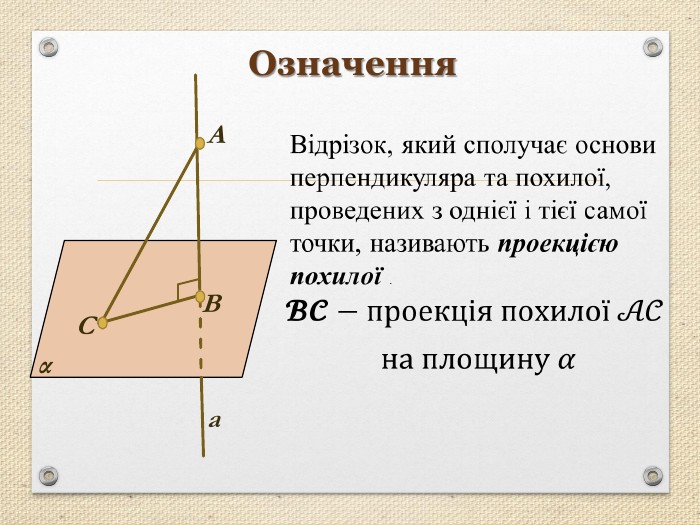
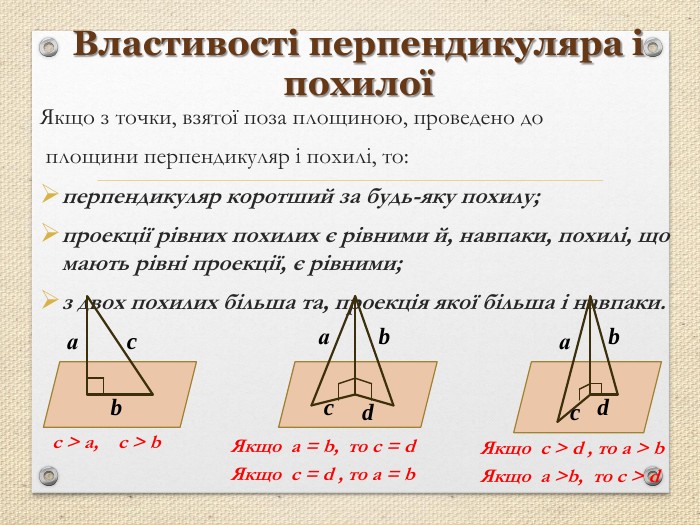
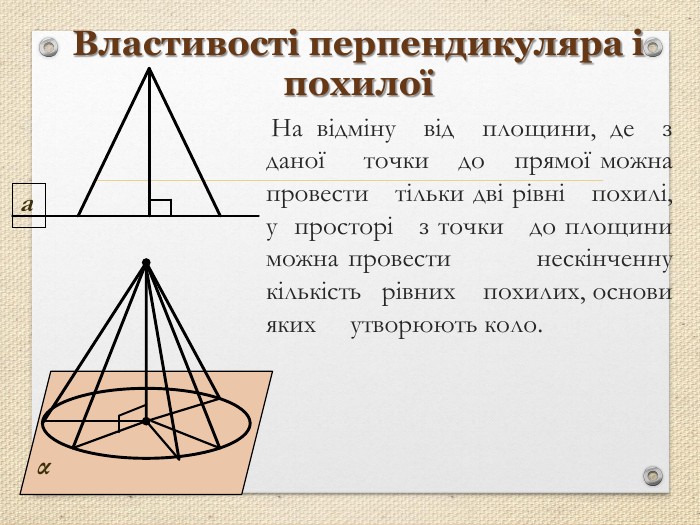
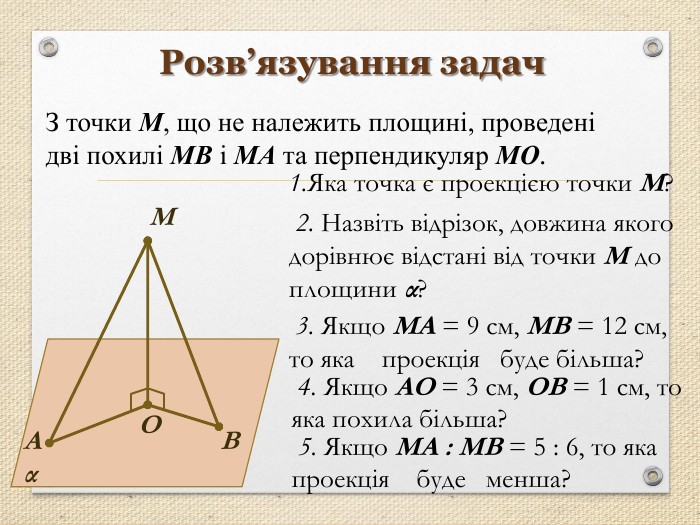
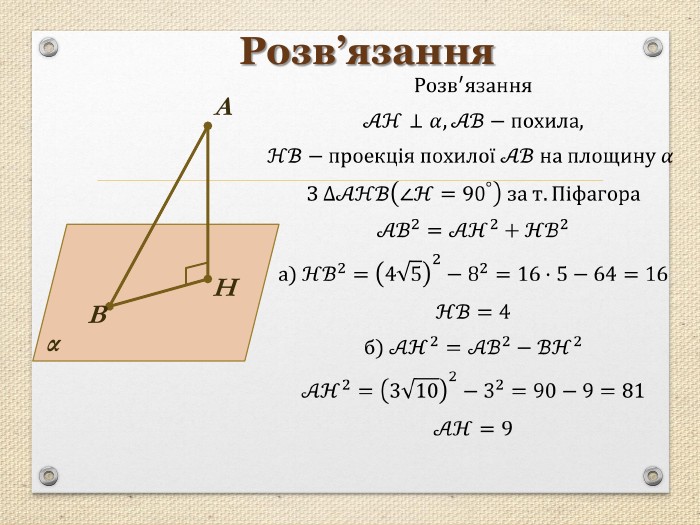
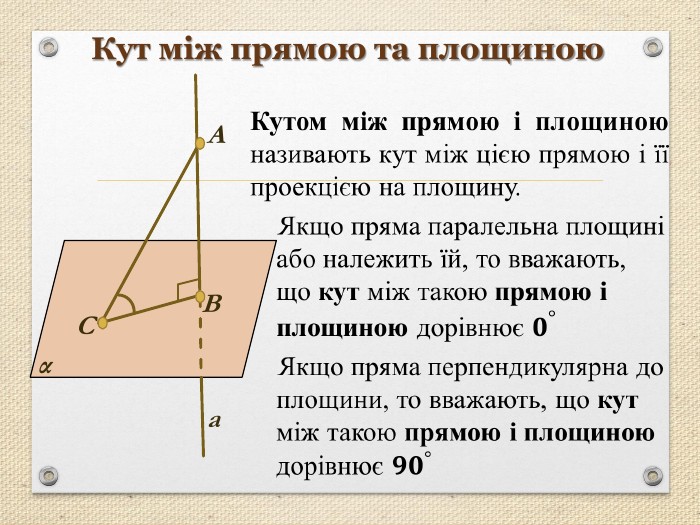
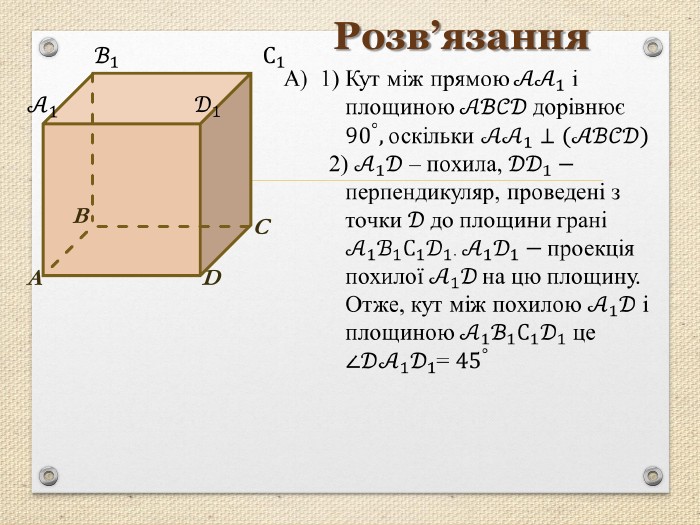
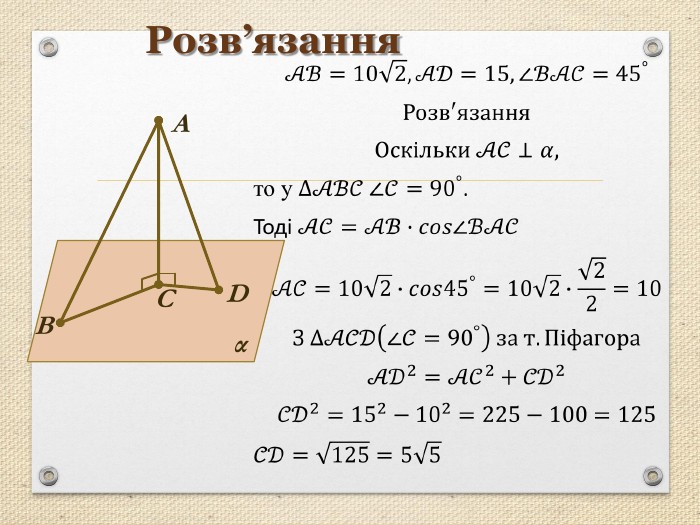
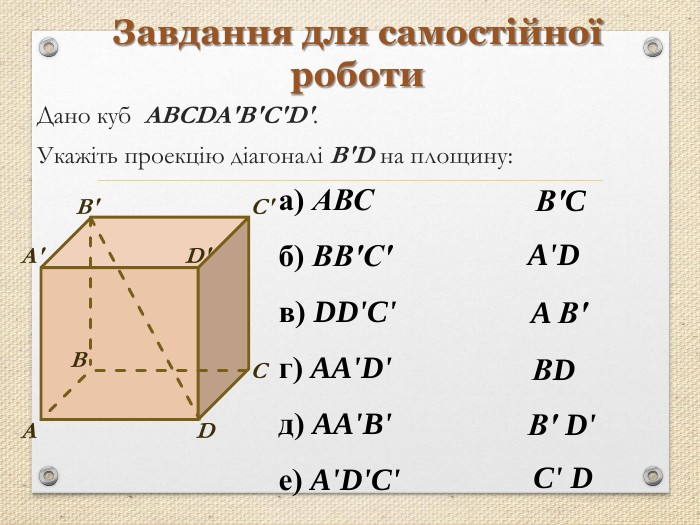
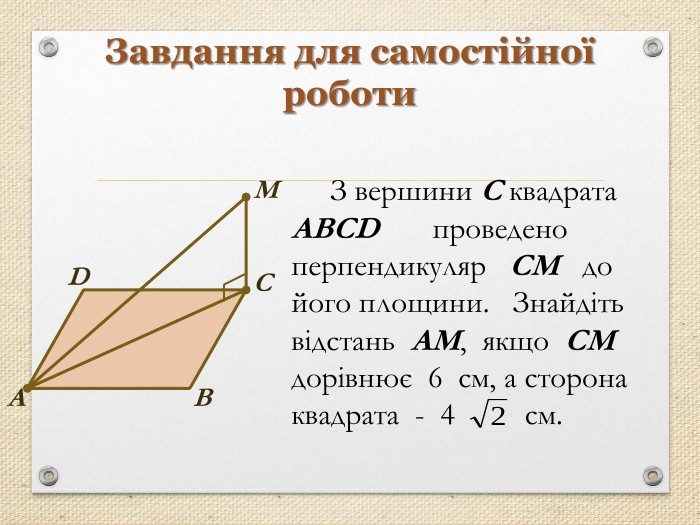
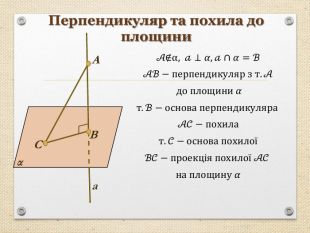
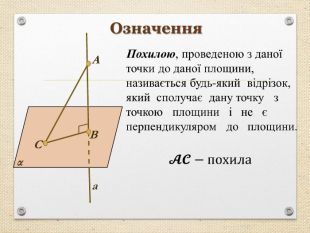
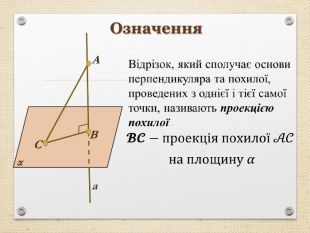
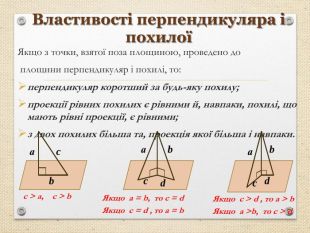
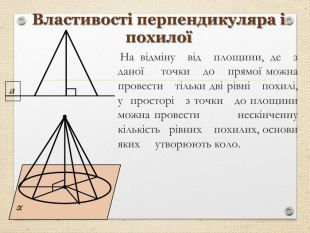
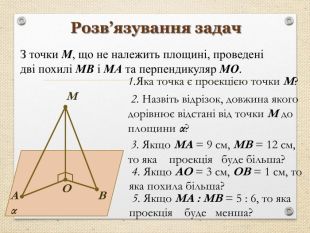
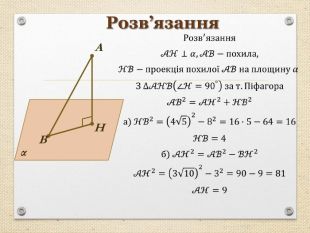
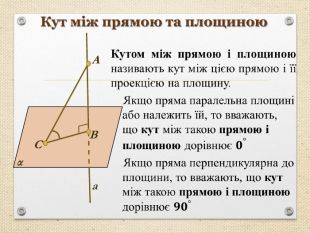
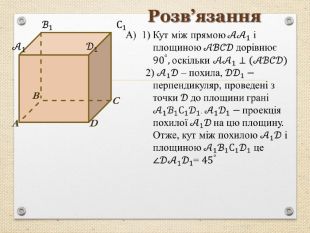
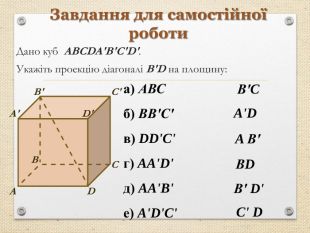
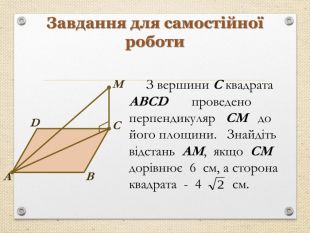
Презентація "Перпендикуляр та похила в просторі"
Про матеріал
Матерал даної презентації буде корисним для опрацювання при підготовці до ЗНО. Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку