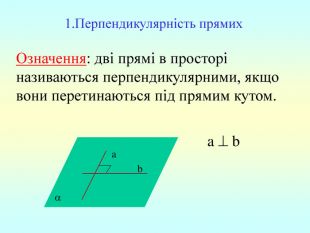
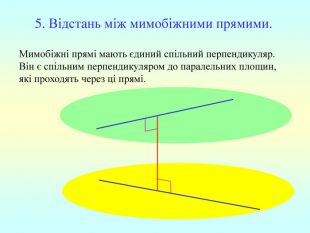
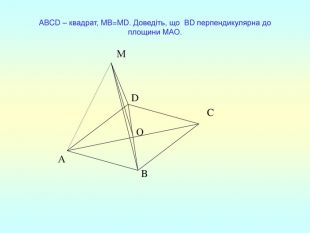
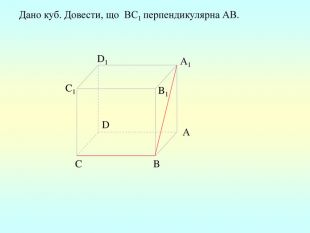
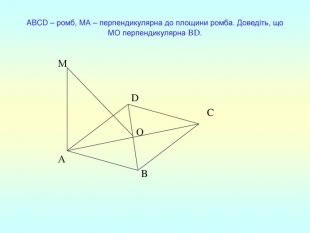
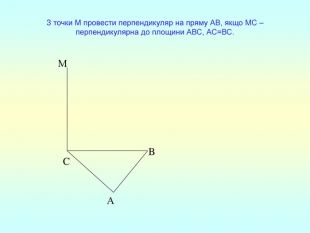
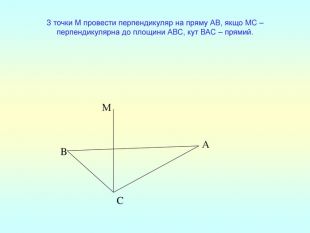
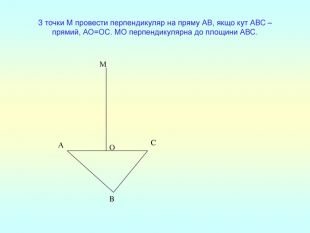
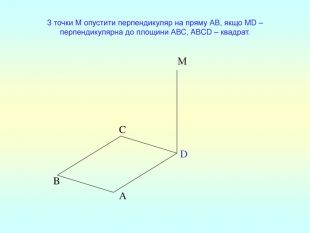
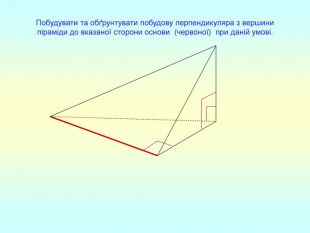
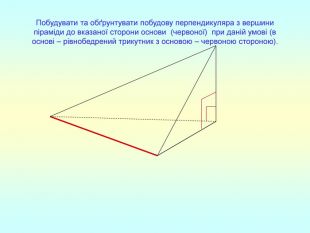
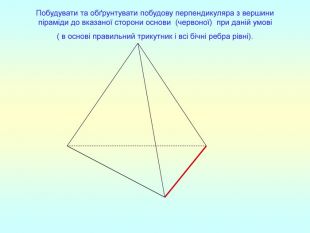
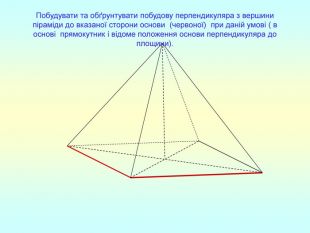
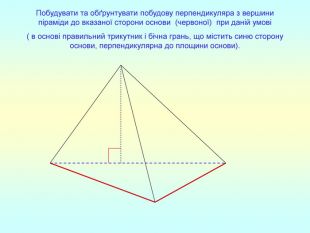
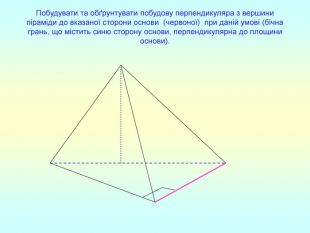
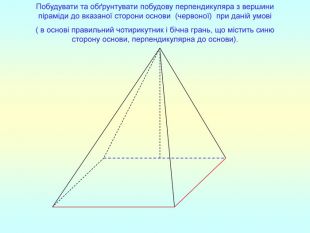
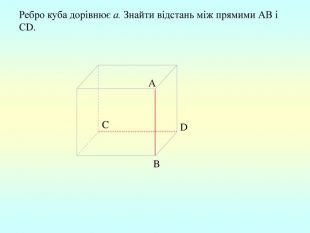
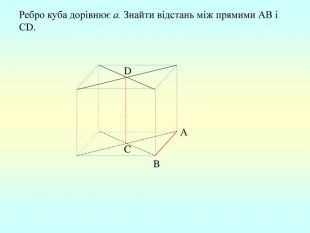
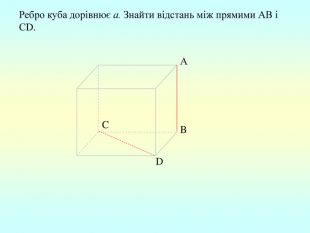
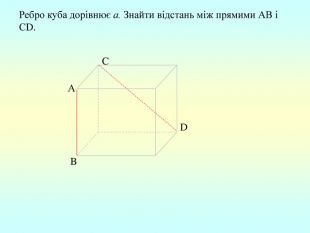
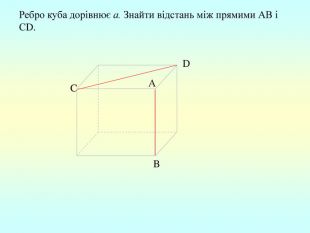
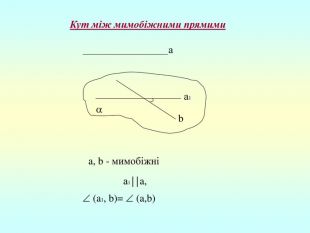
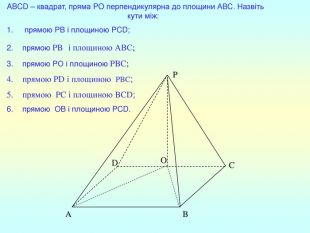
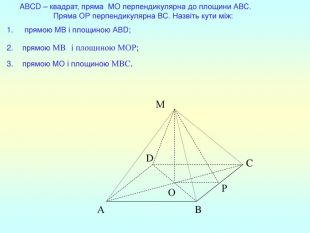
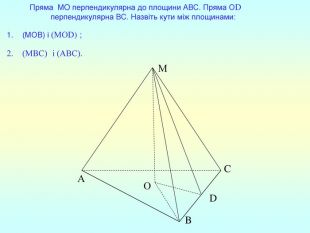
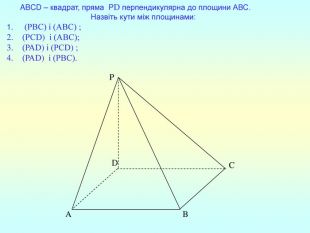
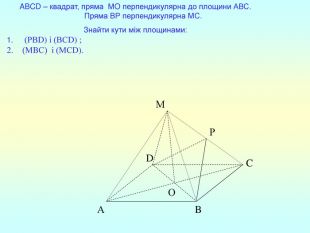
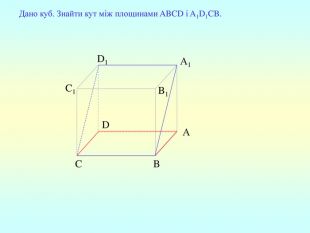
Презентація "Перпендикулярність прямої та площини "

1.Перпендикулярність прямих Означення: дві прямі в просторі називаються перпендикулярними, якщо вони перетинаються під прямим кутом. a b  a  b

Т (ознака перпендикулярності прямих) Дві прямі, що перетинаються і відповідно паралельні двом перпендикулярним прямим, перпендикулярні між собою.  1) Всі чотири прямі лежать в одній площині, то – відома теорема планіметрії. a b a1 b1 ? a∥a1, b ║ b1, a1 b1 ⇒ a  b ? 

2)   a b a1 b1 ? A A1 B B1 O O1 AA1 ∥BB1 ∥OO1.  ∥ -за ознакою. AOO1A1, OBB1O1-паралелограми. За властивістю паралельних площин AB ∥A1B1 ⇒ABB1A1-паралелограм ⇒AO=A1O1,BO=B1O1,AB=A1B1 ⇒ AOB= A1O1B1 за трьома сторонами ⇒ O=O1=900. 

2.Перпендикулярність прямої і площини Означення: пряма перпендикулярна до площини, якщо вона перпендикулярна до будь-якої прямої в цій площині, що проходить через точку їх перетину.  a O a  

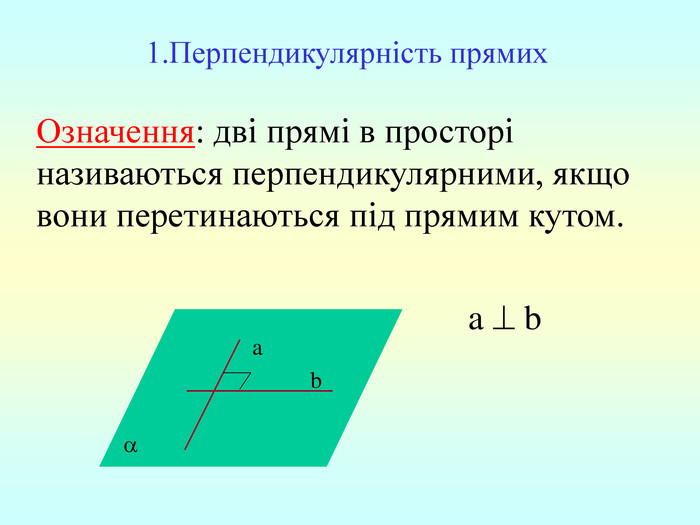
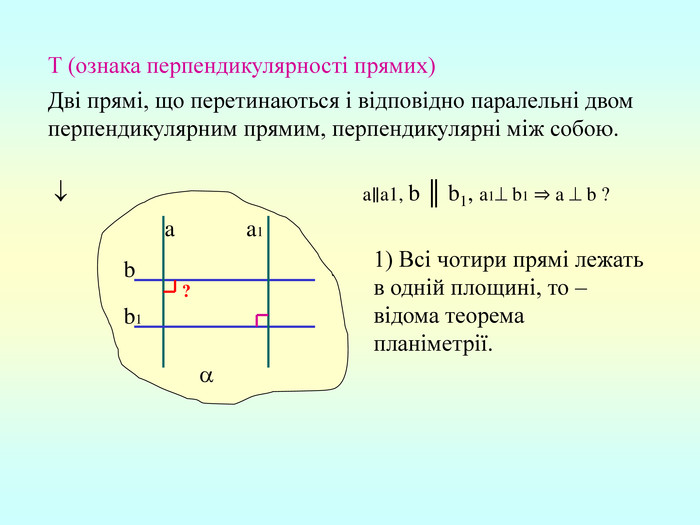
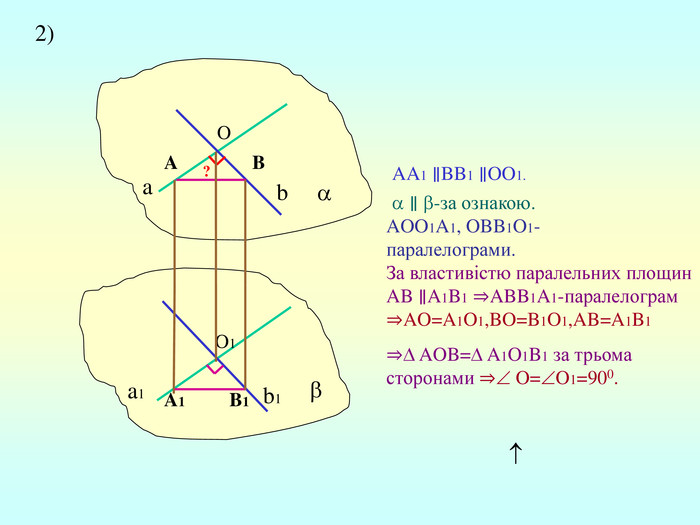
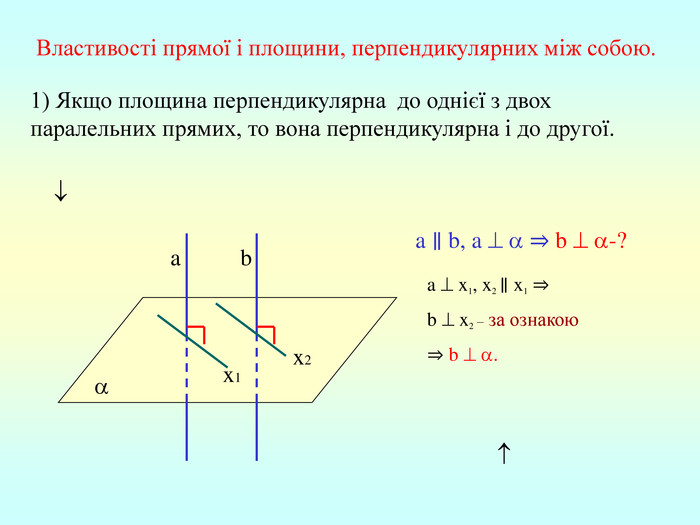
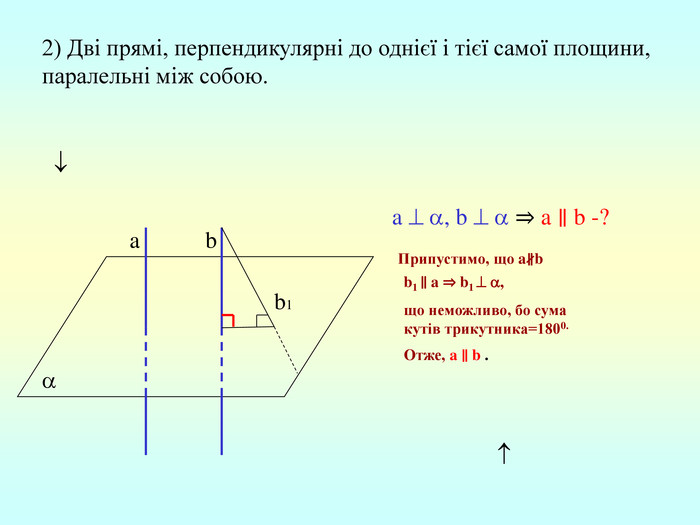
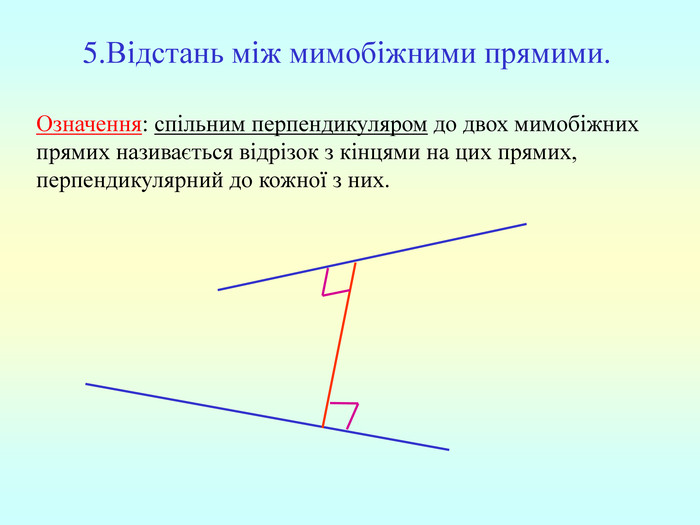
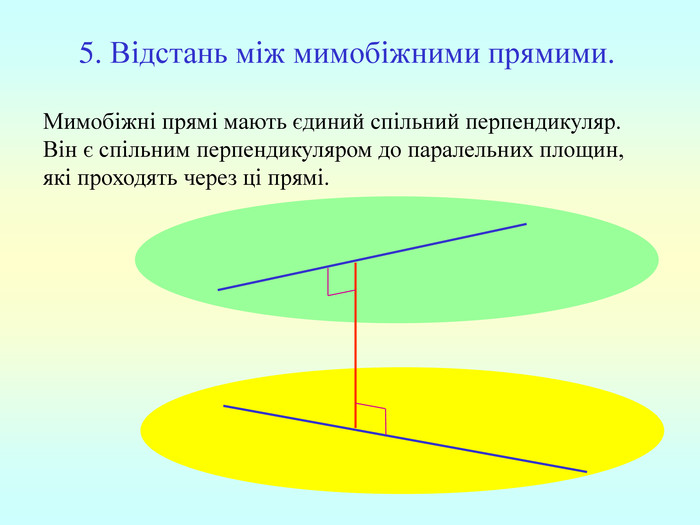
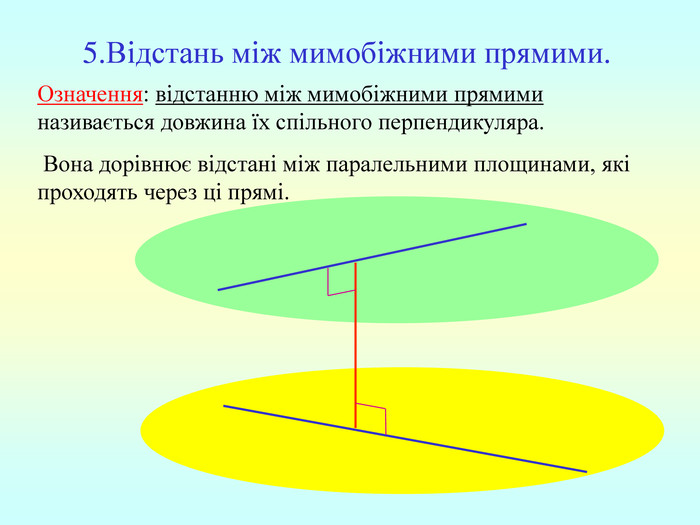
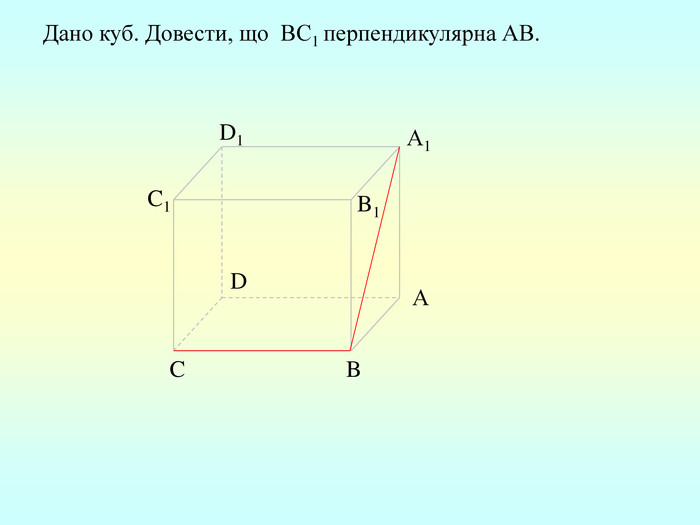
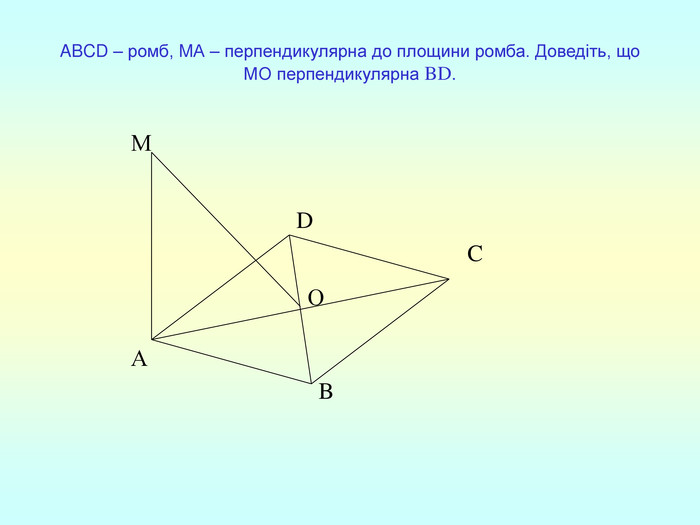
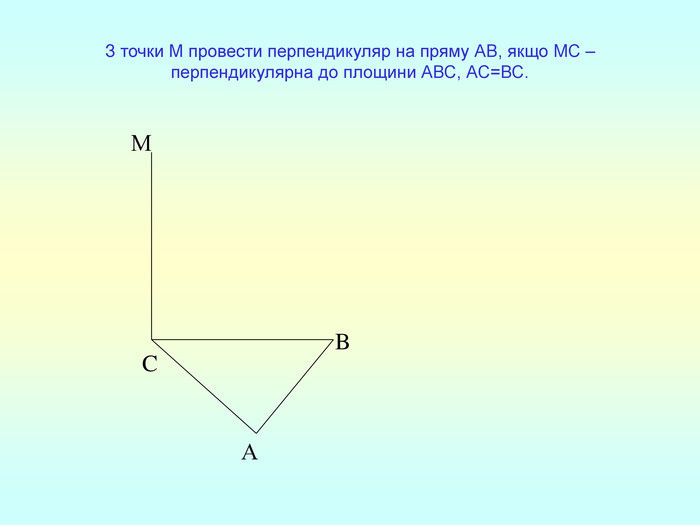
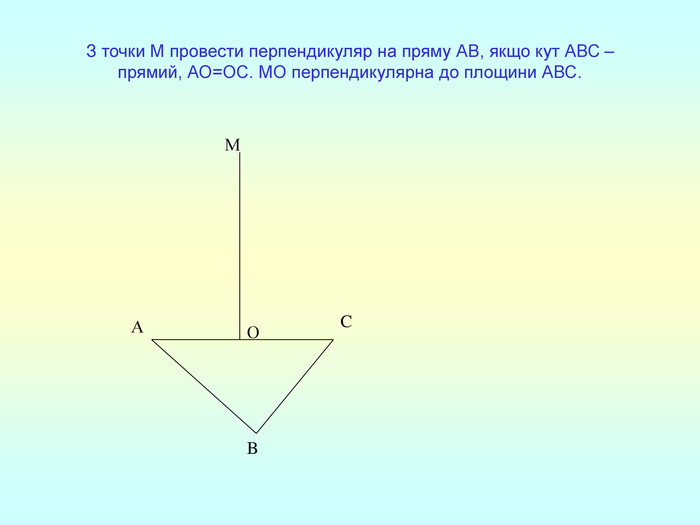
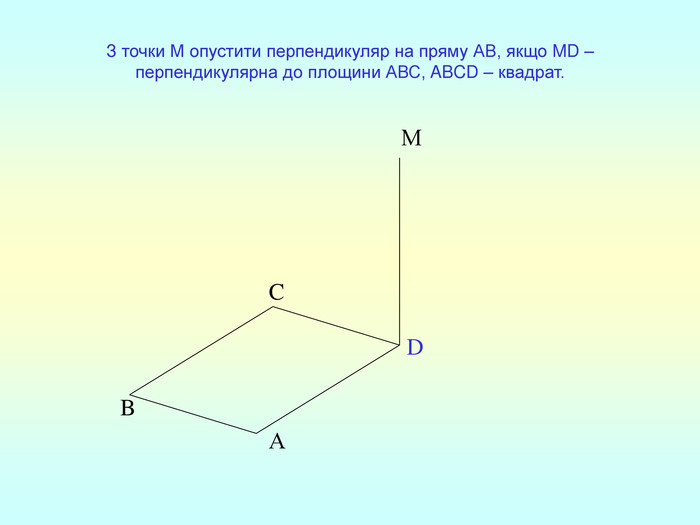
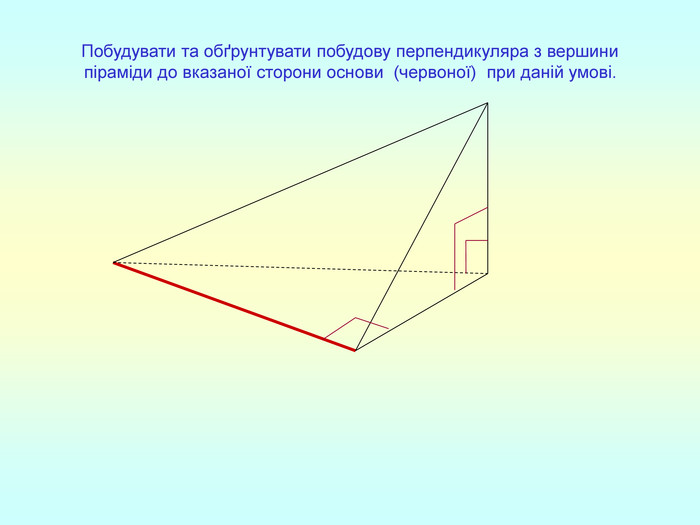
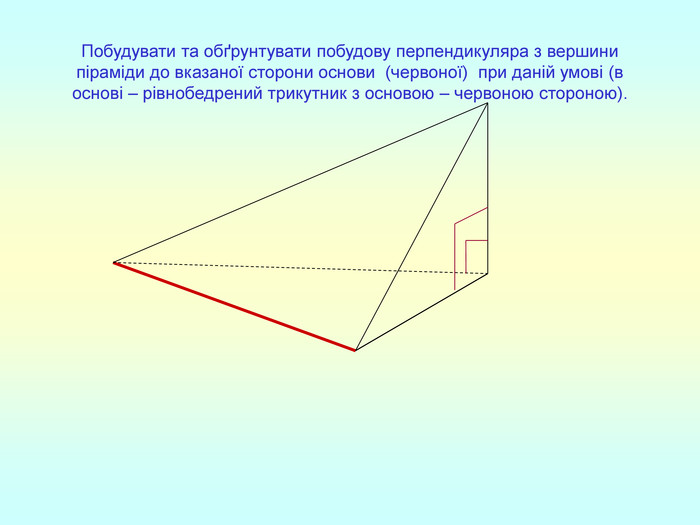
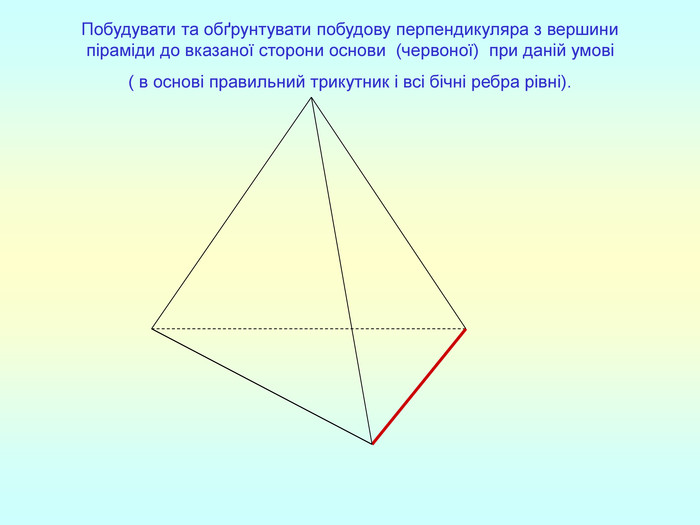
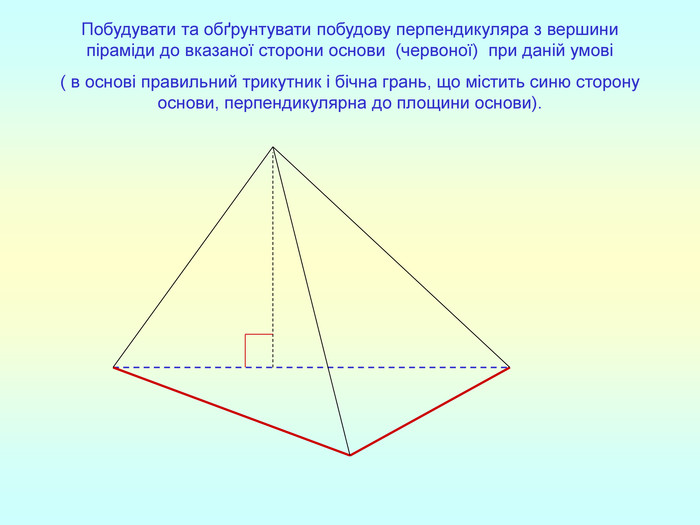
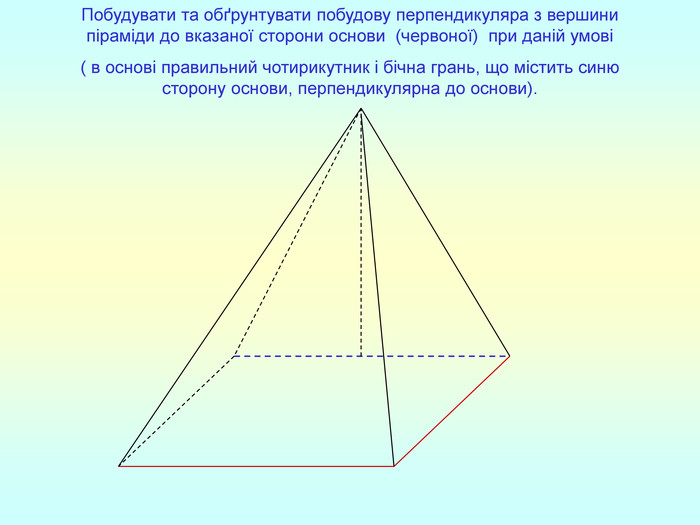
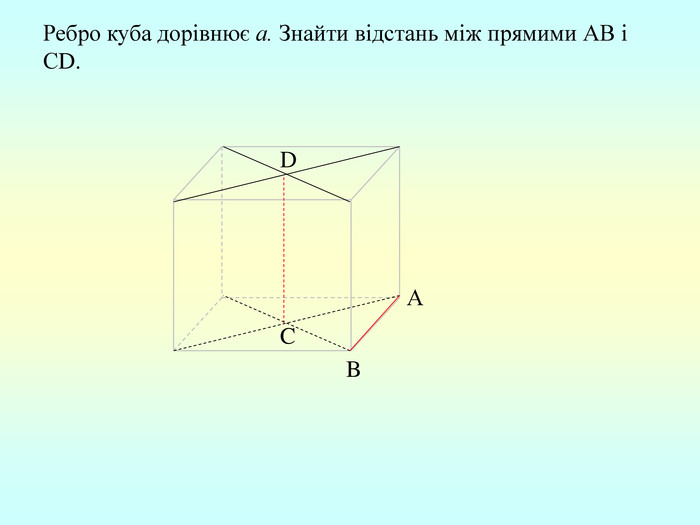
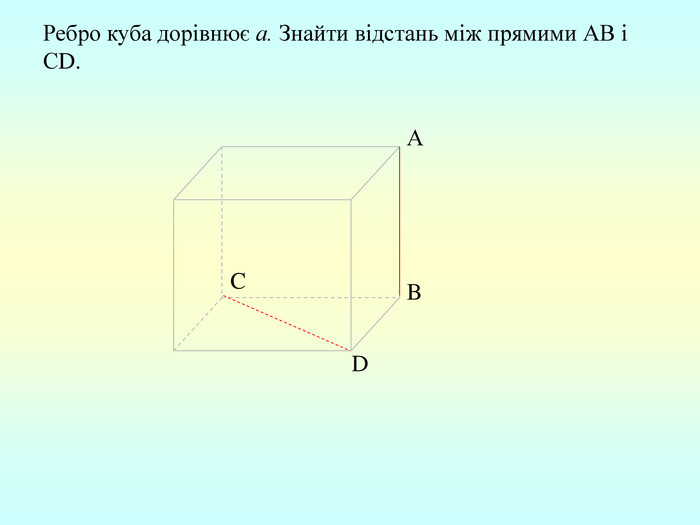
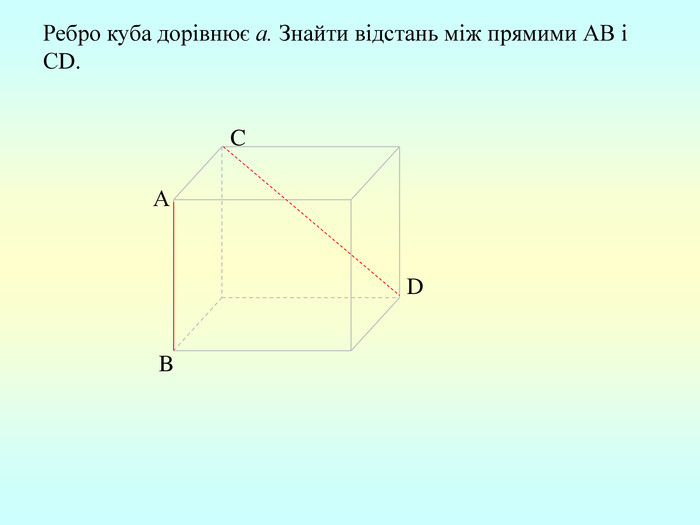
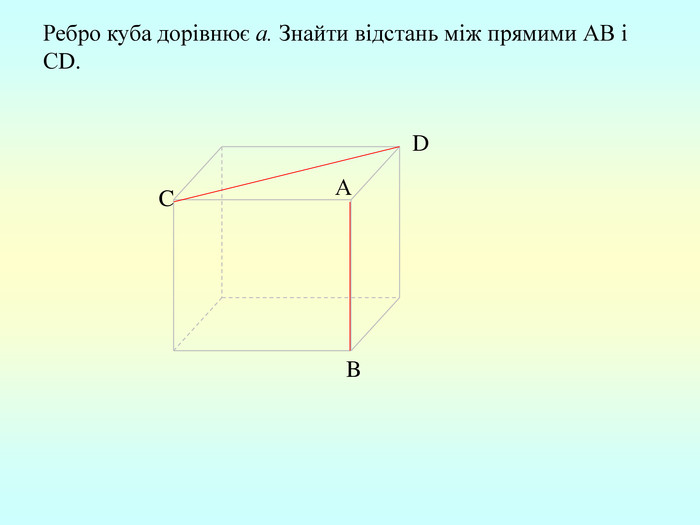
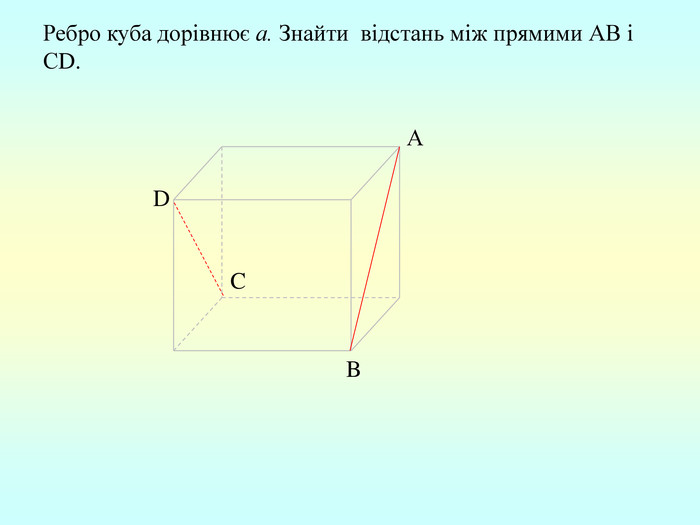
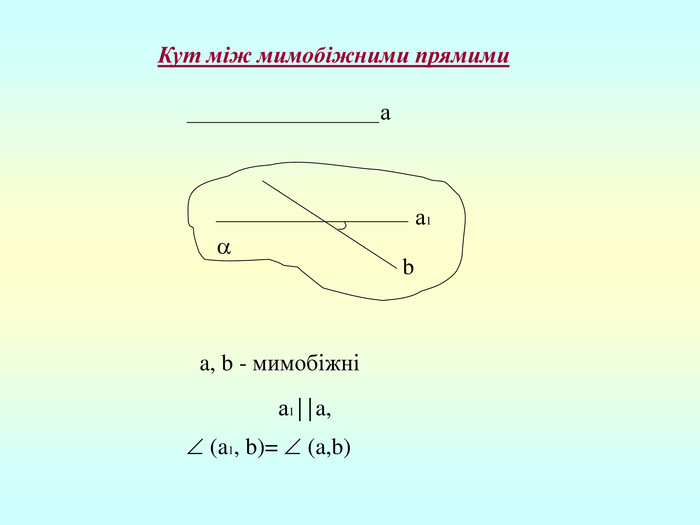
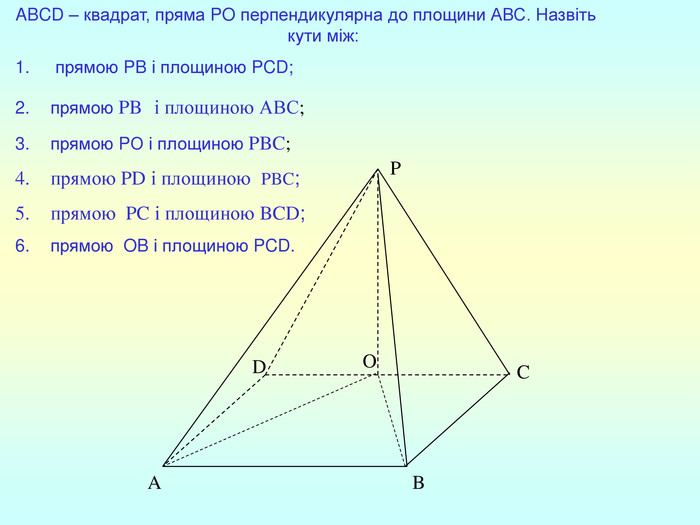
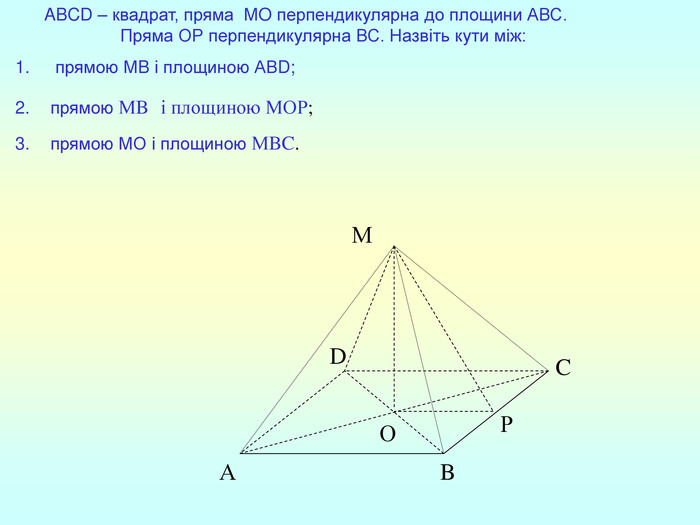
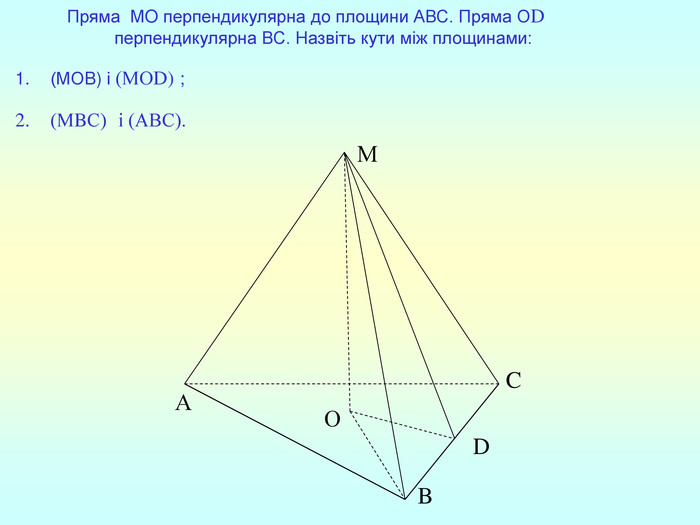
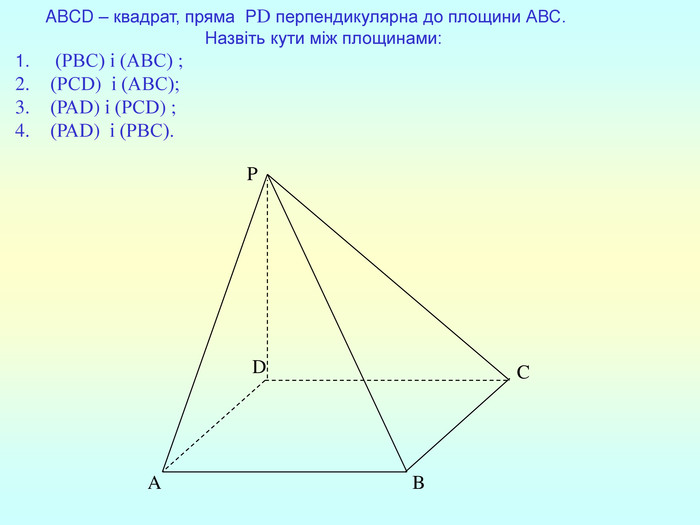
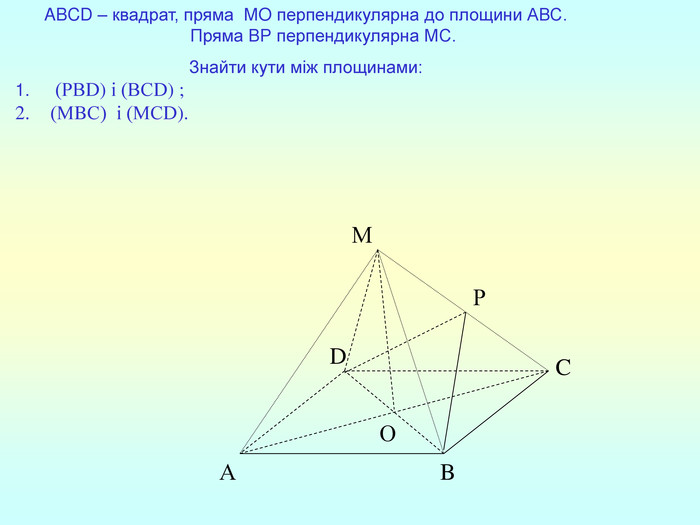
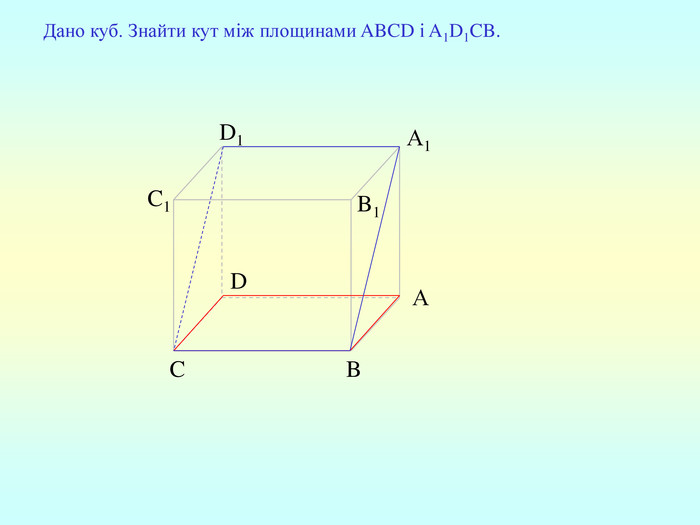
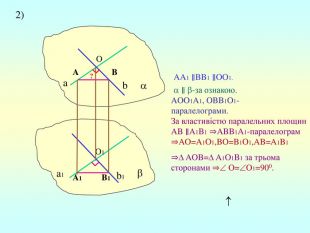
Т(ознака перпендикулярності прямої і площини) Якщо пряма перпендикулярна до двох прямих, які лежать у площині і перетинаються, то вона перпендикулярна до даної площини.  a c,a b ⇒a  -? (a x) 1. A1O= A2O. 2. A1A2C, A1A2B –рівнобедрені (OC,OB-медіани і висоти). 3. A1C=A2C, A2B=A1B. 4. A1CB= A2CB - за трьома сторонами. 5.  A1BC=  A2BC. 6. A1BX= A2BX -за двома сторонами і кутом між ними. 7. A1X=A2X ⇒ A1A2X - рівнобедрений ⇒ OX - медіана ⇒ OX A1A2 (a x).   a c b O x B C X A1 A2 ?

Властивості прямої і площини, перпендикулярних між собою. 1) Якщо площина перпендикулярна до однієї з двох паралельних прямих, то вона перпендикулярна і до другої.  a b a ∥ b, a   ⇒ b  -? x1 x2 a  x1, x2 ∥ x1 ⇒ b  x2 – за ознакою ⇒ b  .  

2) Дві прямі, перпендикулярні до однієї і тієї самої площини, паралельні між собою.  a b  a  , b   ⇒ a ∥ b -? Припустимо, що a∦b b1 b1 ∥ a ⇒ b1  , що неможливо, бо сума кутів трикутника=1800. Отже, a ∥ b . 

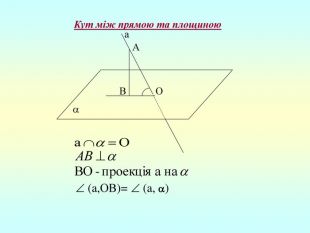
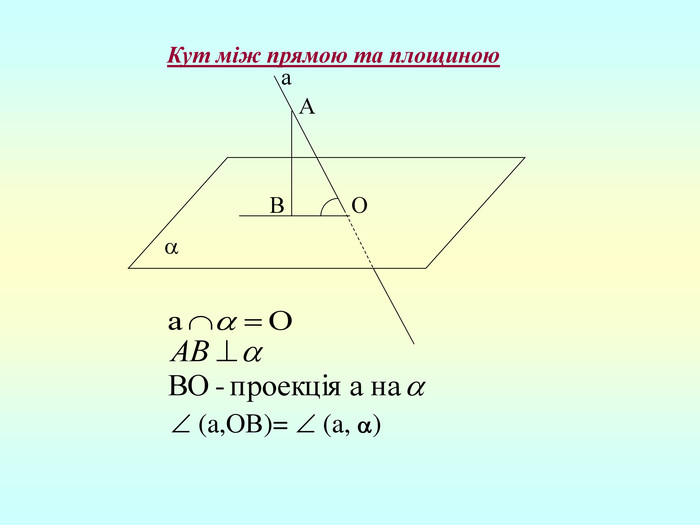
3.Перпендикуляр і похила Означення: 1) Перпендикуляром, проведеним з точки до площини, називається відрізок перпендикулярної прямої, один кінець якого є дана точка, а другий – точка перетину прямої і площини. 2) Похила – будь-який інший відрізок крім перпендикуляра, одним кінцем якого є дана точка, а другим – точка на площині. 3) Відрізок, що сполучає основу похилої і основу перпендикуляра, називається проекцією цієї похилої на площину.  a a   A O AO - перпендикуляр до  О - основа перпендикуляра B AB - похила до  В - основа похилої BO - проекція AB на 

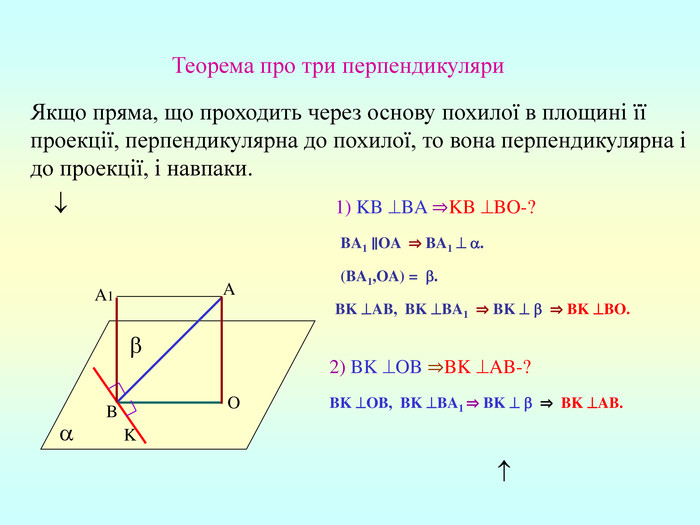
Теорема про три перпендикуляри Якщо пряма, що проходить через основу похилої в площині її проекції, перпендикулярна до похилої, то вона перпендикулярна і до проекції, і навпаки.   K B A O 1) KB BA ⇒KB BO-? A1 BA1 ∥OA ⇒ BA1  .  (BA1,OA) = . 2) BK OB ⇒BK AB-? BK OB, BK BA1 ⇒ BK   ⇒ BK AB.  BK AB, BK BA1 ⇒ BK   ⇒ BK BO.

4.Перпендикулярність площин Означення: дві площини перпендикулярні, якщо третя площина перетинає їх по перпендикулярних прямих і перпендикулярна до лінії їх перетину.    c  ⋂ = a,  ⋂ = b, a  b,   c, ⇒    a b

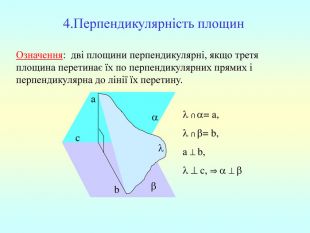
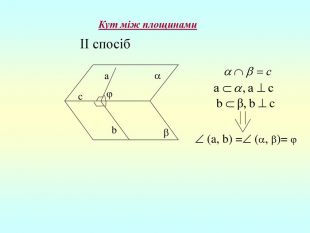
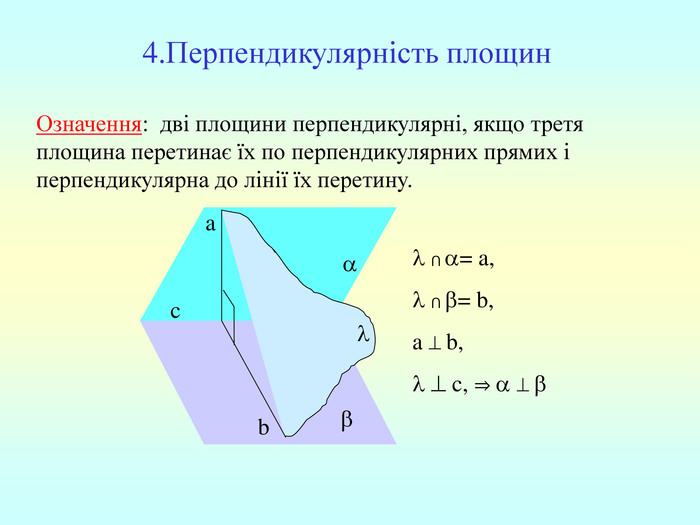
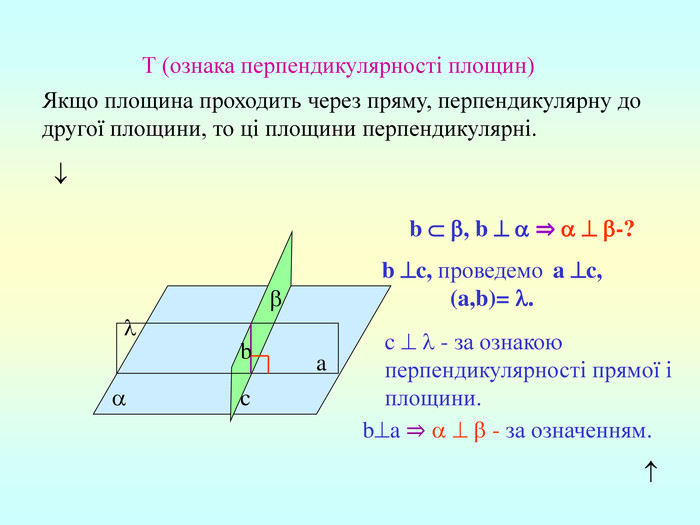
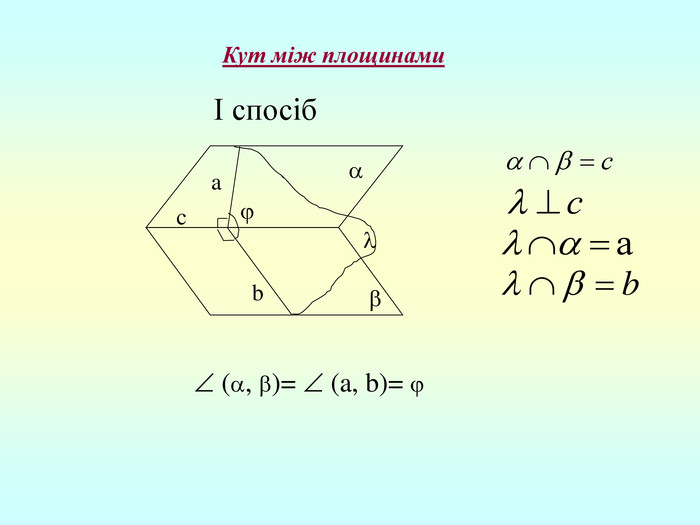
Т (ознака перпендикулярності площин) Якщо площина проходить через пряму, перпендикулярну до другої площини, то ці площини перпендикулярні.   b   a c b  , b   ⇒   -? b c, проведемо a c, (a,b)= . c   - за ознакою перпендикулярності прямої і площини. ba ⇒    - за означенням. 

Властивість прямої, що лежить в одній з двох перпендикулярних площин Якщо пряма, що лежить в одній з двох перпендикулярних площин, перпендикулярна до лінії їх перетину, то вона перпендикулярна і до другої площини.   b  a c b  ,   , b  c ⇒ b   -?  Проведемо a c. =(a,b) ⇒a  b. b c, b a ⇒ b   . 

5.Відстань між мимобіжними прямими. Означення: спільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на цих прямих, перпендикулярний до кожної з них.

5. Відстань між мимобіжними прямими. Мимобіжні прямі мають єдиний спільний перпендикуляр. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі.

5.Відстань між мимобіжними прямими. Означення: відстанню між мимобіжними прямими називається довжина їх спільного перпендикуляра. Вона дорівнює відстані між паралельними площинами, які проходять через ці прямі. 5.Відстань між мимобіжними прямими.

ABCD – паралелограм, MA=MC, MB=MD. Доведіть, що MO перпендикулярна до площини ABC. А B C D О М

ABCD – квадрат, MB=MD. Доведіть, що ВD перпендикулярна до площини МАО. А B C D О М

Дано куб. Довести, що ВС1 перпендикулярна АВ. А B C D А1 B1 C1 D1

ABCD – ромб, MА – перпендикулярна до площини ромба. Доведіть, що МО перпендикулярна BD. А B C D О М

З точки М провести перпендикуляр на пряму АВ, якщо MС – перпендикулярна до площини АВС, АС=ВС. А B C М

З точки М провести перпендикуляр на пряму АВ, якщо MС – перпендикулярна до площини АВС, кут ВАС – прямий. А B C М

З точки М провести перпендикуляр на пряму АВ, якщо кут АВС – прямий, АО=ОС. МО перпендикулярна до площини АВС. А B C М О

З точки М опустити перпендикуляр на пряму АВ, якщо MD – перпендикулярна до площини АВС, ABCD – квадрат. А B C М D

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові.

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові (в основі – рівнобедрений трикутник з основою – червоною стороною).

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові ( в основі правильний трикутник і всі бічні ребра рівні).

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові ( в основі прямокутник і відоме положення основи перпендикуляра до площини).

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові ( в основі правильний трикутник і бічна грань, що містить синю сторону основи, перпендикулярна до площини основи).

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові (бічна грань, що містить синю сторону основи, перпендикулярна до площини основи).

Побудувати та обґрунтувати побудову перпендикуляра з вершини піраміди до вказаної сторони основи (червоної) при даній умові ( в основі правильний чотирикутник і бічна грань, що містить синю сторону основи, перпендикулярна до основи).

Ребро куба дорівнює а. Знайти відстань між прямими АВ і СD. А B C D

Ребро куба дорівнює а. Знайти відстань між прямими АВ і СD. А B C D

Ребро куба дорівнює а. Знайти відстань між прямими АВ і СD. А B C D

Ребро куба дорівнює а. Знайти відстань між прямими АВ і СD. А B C D

Ребро куба дорівнює а. Знайти відстань між прямими АВ і СD. А B C D

Ребро куба дорівнює а. Знайти відстань між прямими АВ і СD. А B C D

а b a, b - мимобіжні а1   (a1, b)=  (a,b) а1 | | a, Кут між мимобіжними прямими

 а О А В  (a,ОВ)=  (a, ) Кут між прямою та площиною

І спосіб    c a b   (, )=  (a, b)=  Кут між площинами

ІІ спосіб   c a b   (a, b) = (, )=  Кут між площинами

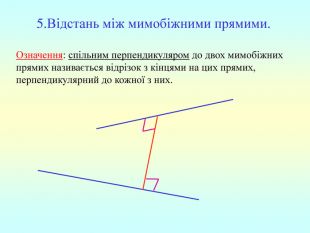
Площа ортогональної проекції багатокутника на площину дорівнює добутку площі самого багатокутника на косинус кута між площиною багатокутника і площиною його проекції.   А О В С К ВОС – проекція АВС на  АК – похила ОК - проекція АК на  за теоремою про 3 перпендикуляри ОК  ВС АКО=-кут між (АВС) і  

ABCD – квадрат, пряма PO перпендикулярна до площини АВС. Назвіть кути між: прямою PB і площиною PCD; прямою PB і площиною АВС; прямою PО і площиною PBC; прямою PD і площиною PBC; прямою PC і площиною BCD; прямою OB і площиною PCD. A D B C P O

ABCD – квадрат, пряма МO перпендикулярна до площини АВС. Пряма ОР перпендикулярна ВС. Назвіть кути між: прямою МB і площиною АВD; прямою МB і площиною МОР; прямою МО і площиною МBC. А B C D О М Р

А B C D О М Пряма МO перпендикулярна до площини АВС. Пряма ОD перпендикулярна ВС. Назвіть кути між площинами: (МОB) і (МОD) ; (МBС) і (АВС).

ABCD – квадрат, пряма PD перпендикулярна до площини АВС. Назвіть кути між площинами: (РВС) і (АВС) ; (РСD) і (АВС); (РАD) і (РСD) ; (РАD) і (РВС). A D B C P

ABCD – квадрат, пряма МO перпендикулярна до площини АВС. Пряма ВР перпендикулярна МС. Знайти кути між площинами: (РВD) і (ВСD) ; (МBС) і (МСD). А B C D О М Р

Дано куб. Знайти кут між площинами ABCD і A1D1CB. А B C D А1 B1 C1 D1