Презентація "Піраміда як многогранник"
Про матеріал
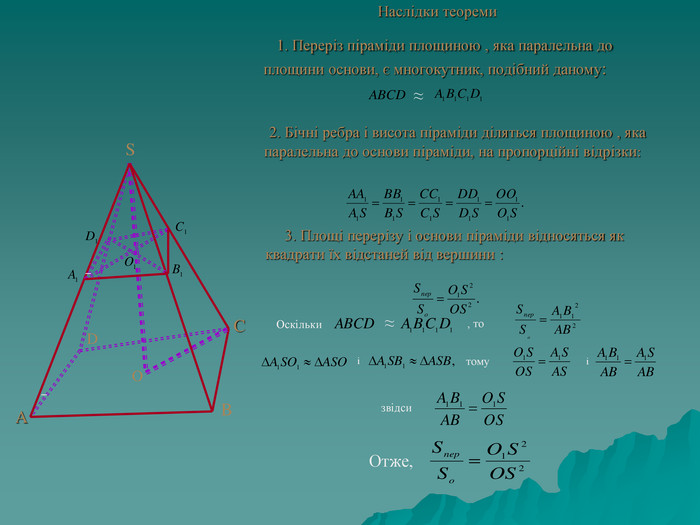
Презентація містить задачі, що стосуються теми "Піраміда, її поверхня та об'єм". Створена для формування практичних навичок учнів по даній темі Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку