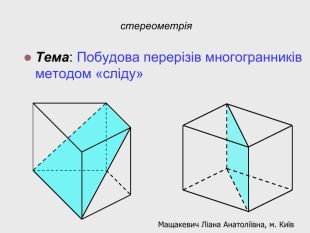
Презентація " Побудова перерізів многогранників (ознайомлення)"
Про матеріал
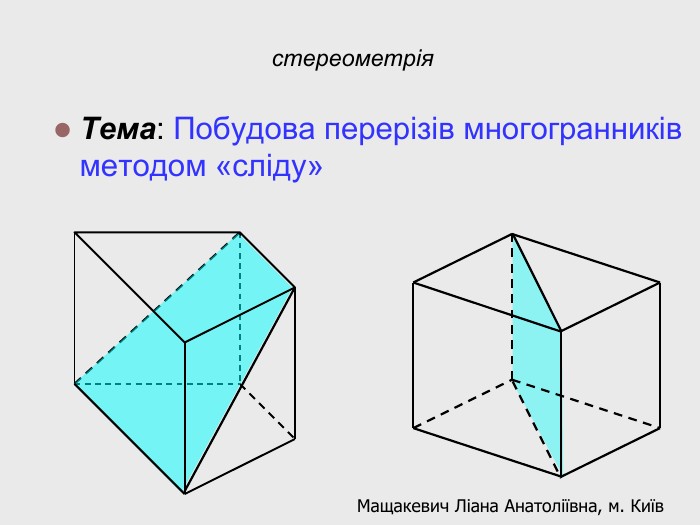
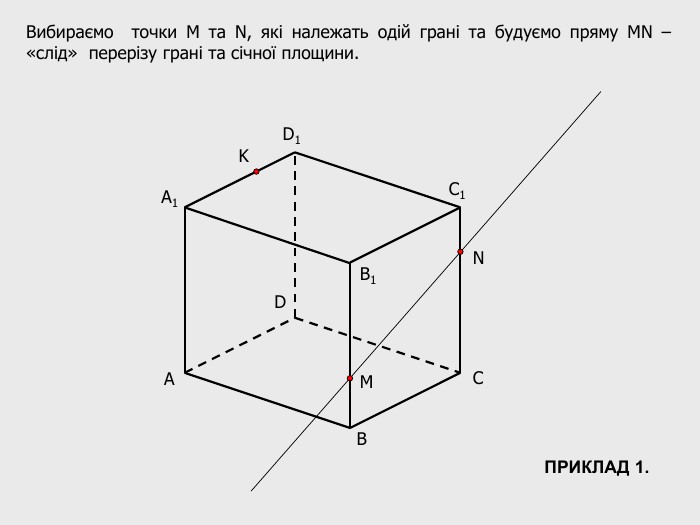
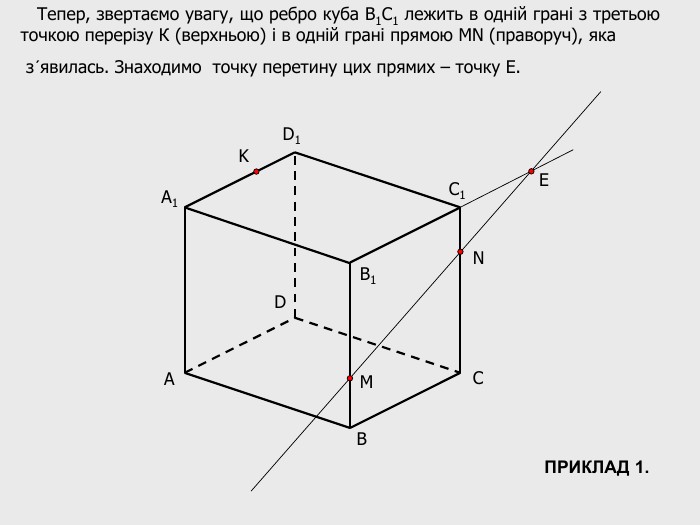
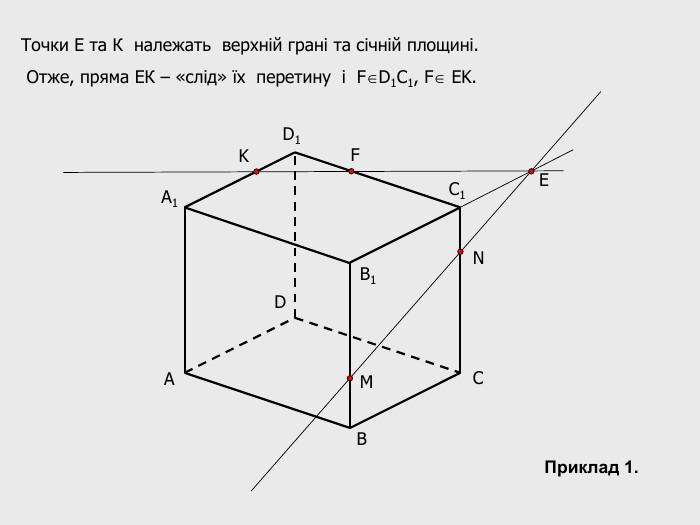
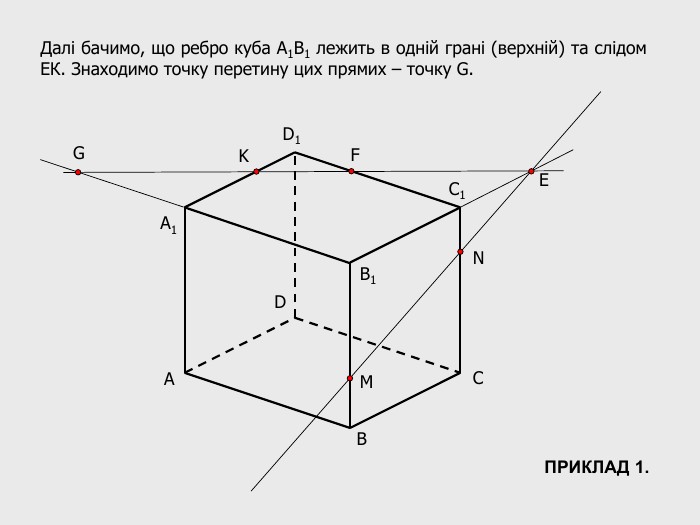
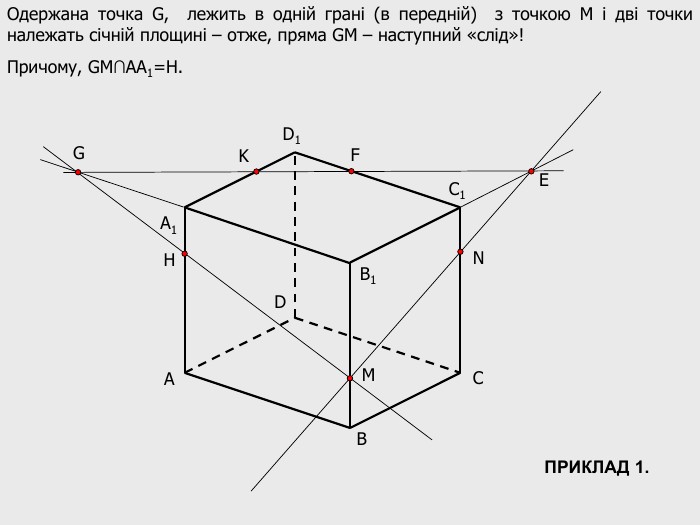
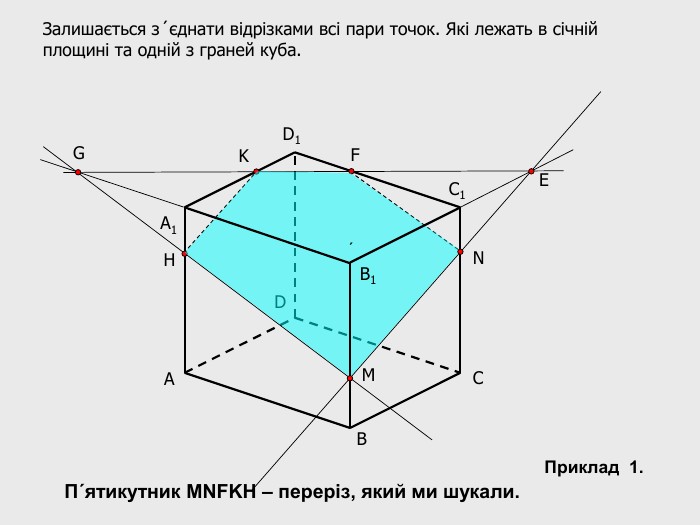
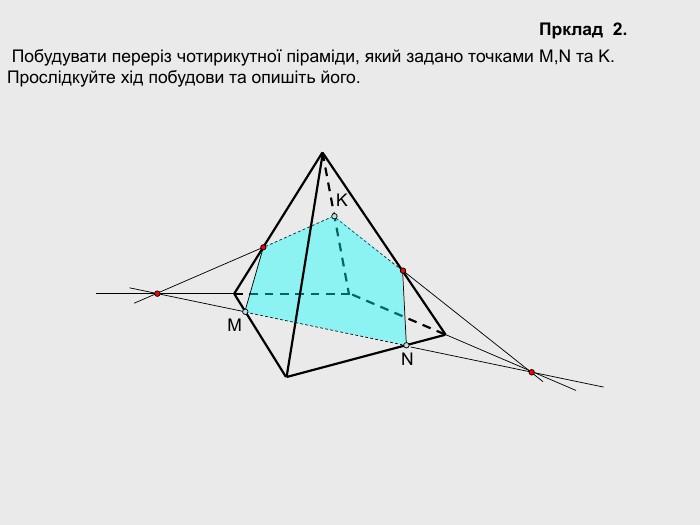
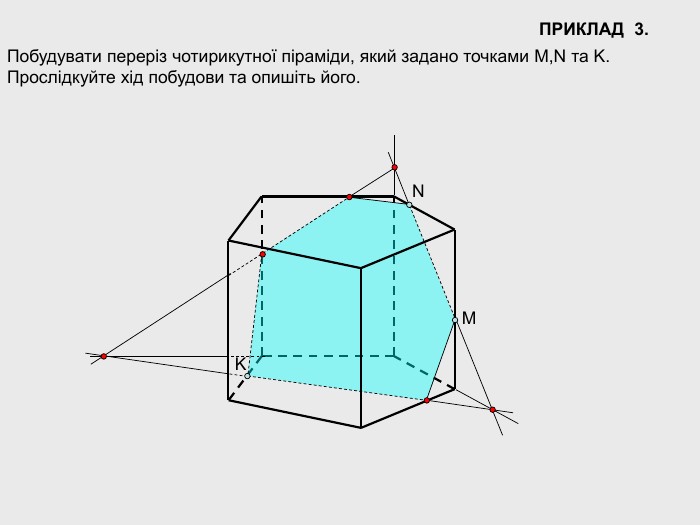
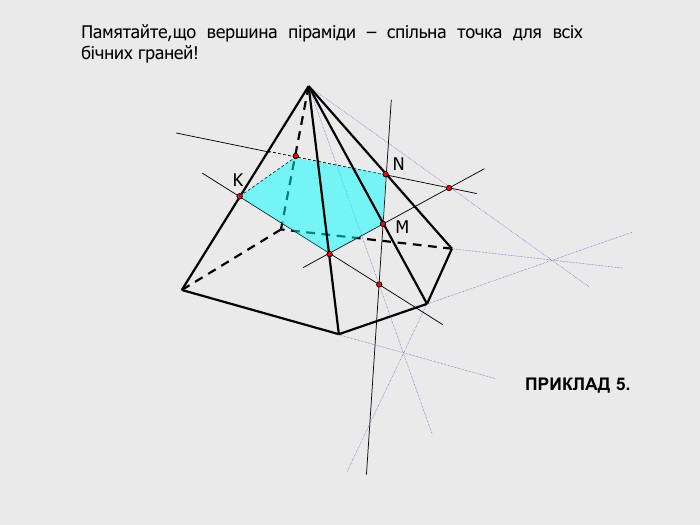
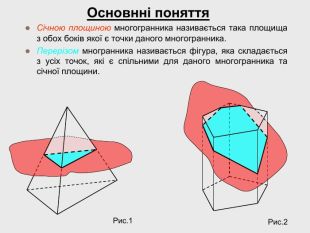
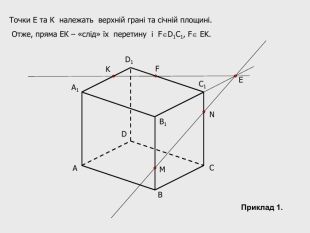
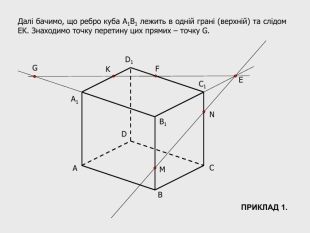
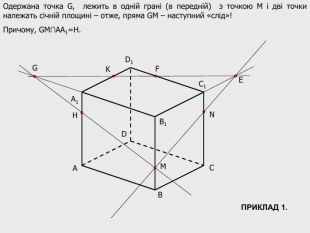
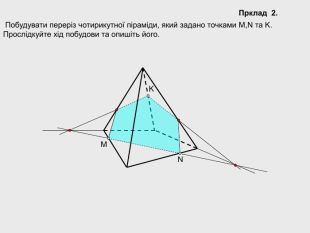
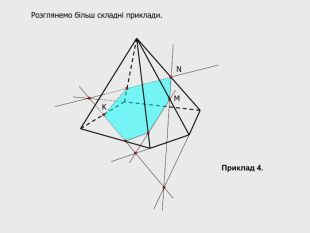
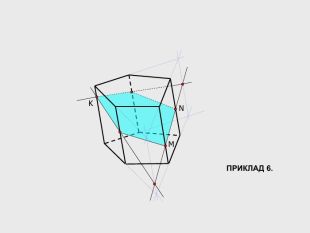
В анімованій презентації на тему "Побудова перерізів многогранників" розглянуто метод "сліду" на прикладі перерізу куба. Також, представлені завдання з розвязками на закріплення різного рівня складності.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку