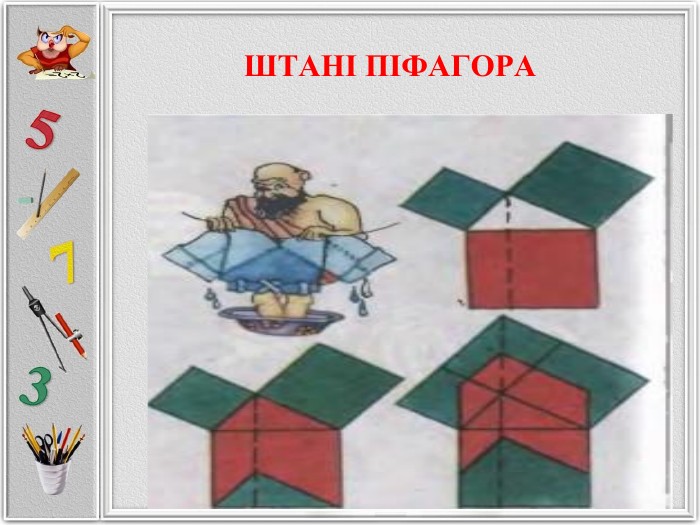
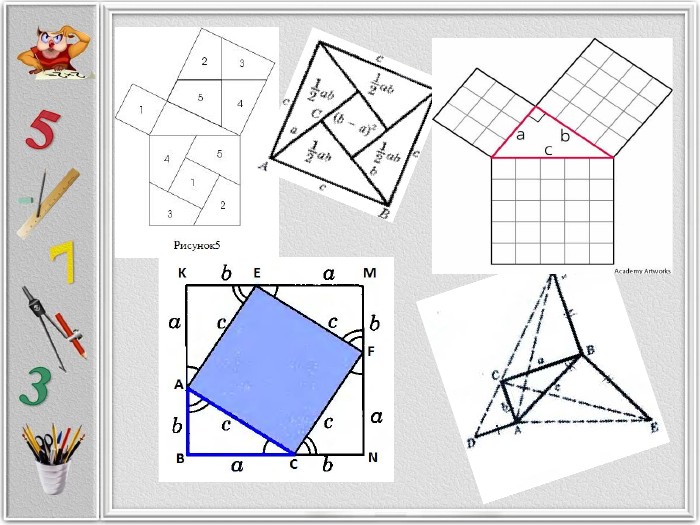
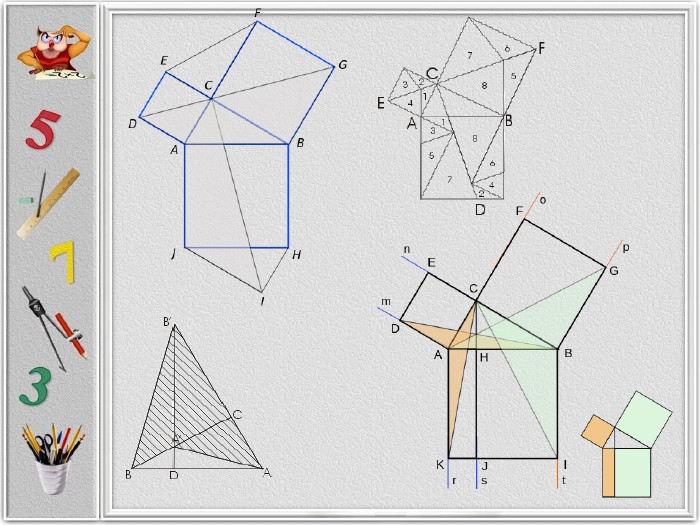
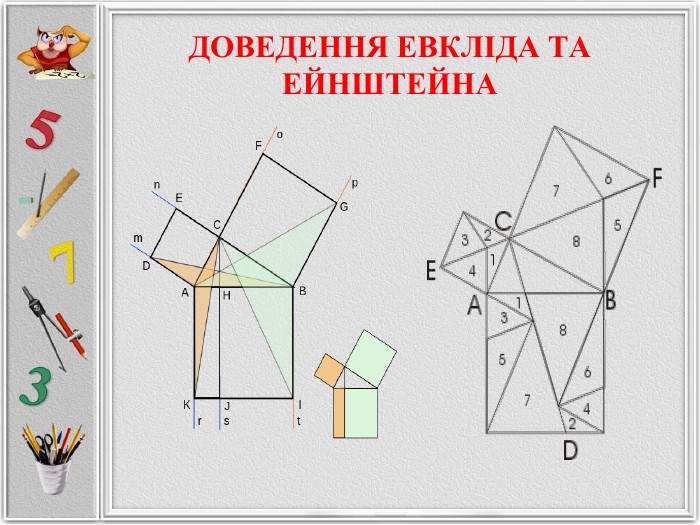
Презентація "Проста і загадкова теорема Піфагора"
Про матеріал
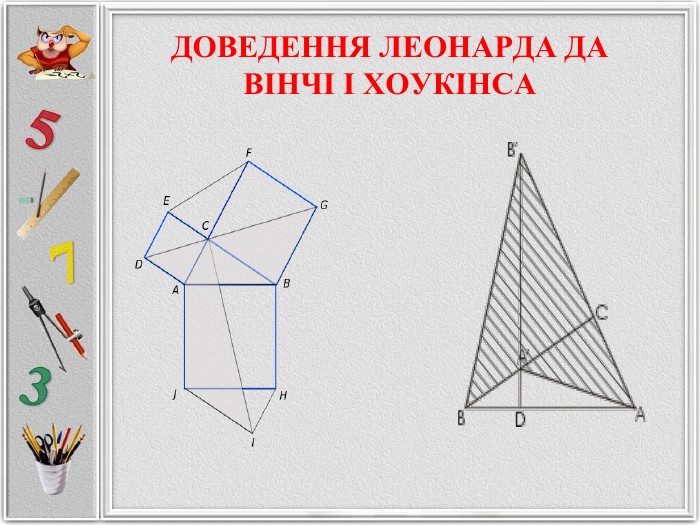
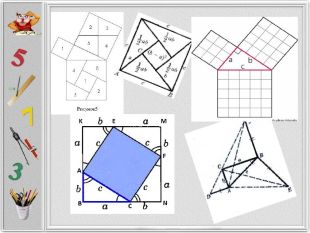
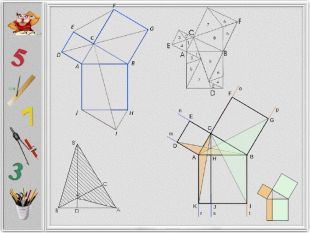
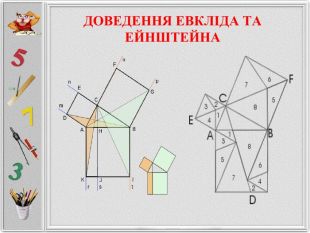
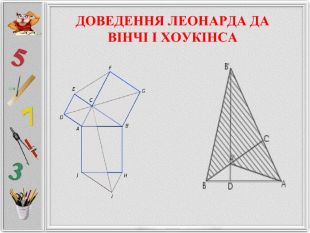
Презентація створена для розширення відомостей про способи доведення теореми Піфагора, які не роглядаються на уроках геометріі. Матеріал може бути використаних на гуртвових заняттях з математики. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку