Презентація "Подібні трикутники"
Про матеріал
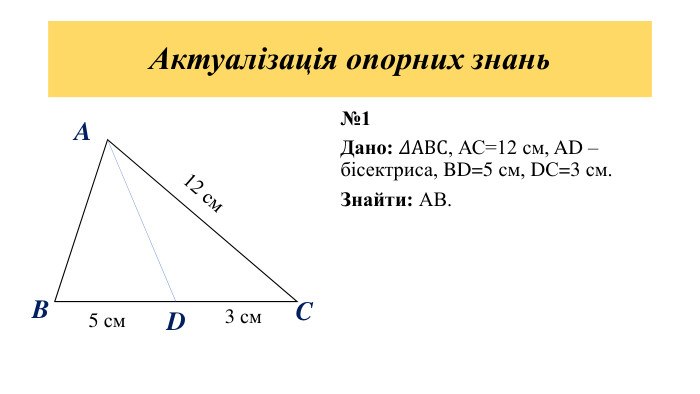
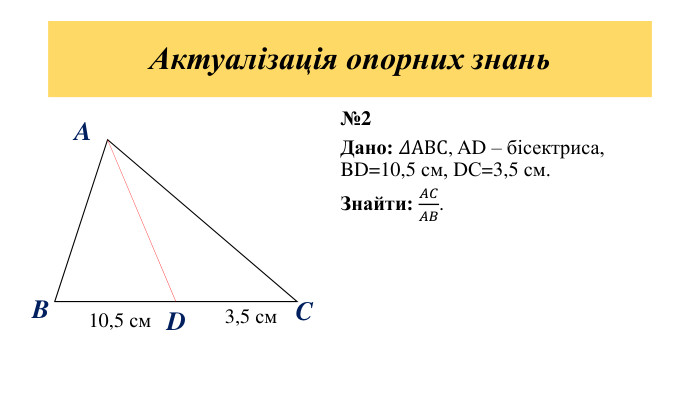
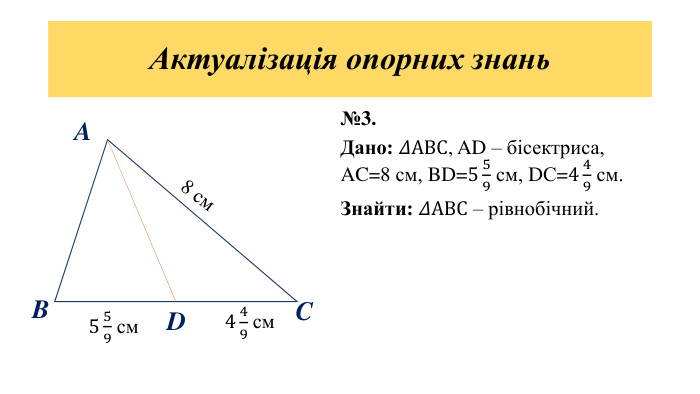
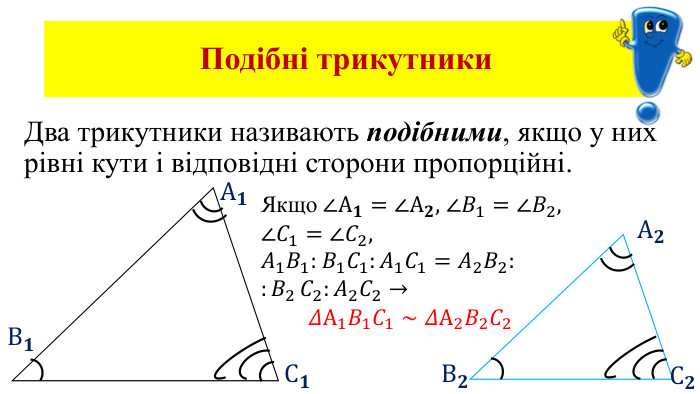
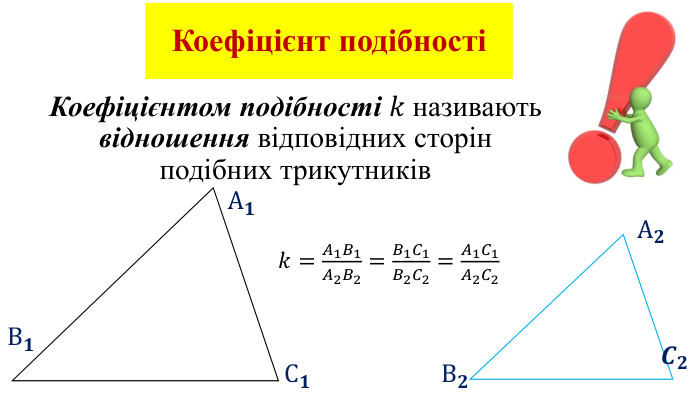
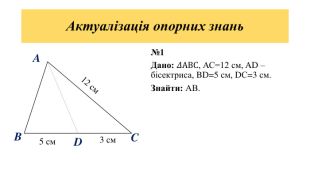
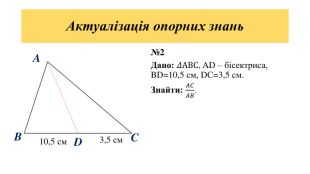
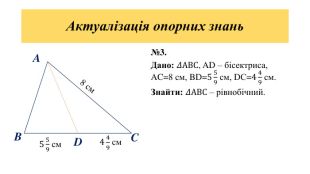
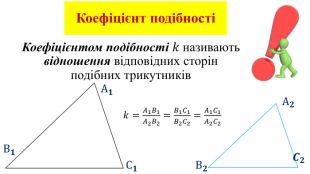
Дана презентація є допоміжним матеріалом для уроку з геометрії на тему "Подібність трикутників" . У ній пояснюється означення подібних фігур, подібних трикутників, коефіцієнта подібності; наявні завдання на повторення властивості бісектриси трикутника та на подібність трикутників.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку