Презентація «Прогалини в знаннях учнів та їх запобігання»

Прогалини в знаннях учнів та їх запобігання. Виконала: вчитель математики. КУ ССШ І-ІІІ ст. №10м. Суми

ЗМІСТ ТЕМА: Прогалини в знаннях учнів та їх запобігання. Вступ………………………………………………………………………………………........3 РОЗДІЛ І Теоретичні обґрунтування неуспішності…………………………………..51.1 Ознаки та причини прогалин в знаннях учнів………………….............................51.2 Психологічна характеристика «неуспішних» учнів ……………………………..91.3 Класифікація причин виникнення прогалин в знаннях учнів…………….….12 РОЗДІЛ ІІ Шляхи подолання прогалин в знаннях учнів….……………………..…152.1 Профілактика неуспішності………………………………………………………….152.2 Надання допомоги учням з низьким рівнем підготовки…………………..…..172.3 Удосконалення уроку………………………………………………………..………...192.4 Робота над помилками як одна із форм подолання прогалин у знаннях і вміннях учнів……………………………………………………………...…................222.5 Шляхи подолання неуспішності…………………………………………….………29 ВИСНОВКИ…..……………………………………………………………………….……….34 СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ...……………………………………………..........37 ДОДАТКИ

Актуальність теми дослідження. Однією із найбільш гострих проблем сучасної школи, від якої чи не найбільш потерпає наше суспільство, продовжує залишатися проблема розвитку пізнавальної активності і запобігання неуспішності школярів. Неуспішність учнів – це огріх школи. Школа, у якій є невстигаючі учні, – це школа, що випускає брак, що працює недостатньо ефективно. Школа несе моральну відповідальність перед невстигаючими учнями, тому що вона не зуміла дати їм потрібне виховання й освіту, вона зробила їх невдахами і тим самим скалічила їхню подальшу долю. Школа несе відповідальність перед батьками невстигаючих учнів, тому що батьки віддали своїх дітей у школу в надії, що вона виховає їх як моральних, культурних, творчо активних і соціально зрілих особистостей, а школа замість цього зробила цих дітей невдахами, ізгоями суспільства. Школа несе відповідальність за неуспішність учнів і перед суспільством і державою, тому що суспільство і держава доручили школі підготувати гідне нове покоління, що зможе здійснити подальший прогрес і розвиток країни, а школа замість цього випускає браковану продукцію – випускників, що погано підготовлені для дорослого життя, для творчої діяльності на благо суспільства і держави.

Об’єктом дослідження є прогалини в знаннях учнів і, як результат постійного відставання, - неуспішність як психолого-педагогічне явище, предметом – причини неуспішності учнів. Завданнями роботи є: – вивчення та виділення причин однієї із найактуальніших проблем сучасної освіти – прогалини в знаннях учнів, і, як результат, неуспішность школярів, її попередження та профілактики; – дослідження неуспішності учнів; – запропонувати шляхи запобігання прогалин в знаннях учнів, попередження неуспішності.

У процесі роботи були використані такі методи: - вивчення педагогічної і методичної літератури; - спостереження за процесом контролю у навчанні математики; - аналіз та узагальнення досвіду роботи вчителів; - експеримент, цілі якого полягали у запобіганні прогалин в знаннях учнів, і, як результат, попередження неуспішності учнів; - експериментальне проведення уроків – рольових ігор, роботи в парах, інтерактивних уроків, проведення домашніх навчальних робіт тощо; статистичний аналіз отриманих результатів. В даному дослідженні висувається припущення про те, що педагог може надати допомогу в подоланні труднощів, що виникають в учбовій діяльності, знаючи конкретні психологічні причини цих труднощів і будуючи розвиваючі роботи на цій основі.

ВИСНОВКИ Прогалини в знаннях учнів, і, як результат, неуспішність - це складне і багатогранне явище шкільної дійсності, що вимагає різносторонніх підходів при його вивчені. В цій роботі зроблено спробу розглянути неуспішність, як результат прогалин в знаннях учнів, в зв’язку з основними категоріями дидактики – змістом і процесом навчання. На основі всього вище сказаного можна зробити такі висновки: Ефективність навчання визначається в остаточному підсумку характером відносини учнів до навчання, характером їхньої навчальної роботи.2. Навчальний процес повинний проводитися в органічній єдності колективних, фронтальних та індивідуальних форм навчальних занять при визначальному характері загальної колективної діяльності учнів.3. Для того щоб вчасно виявляти будь-які прогалини в навчанні кожного учня і відразу його заповнювати, поточний контроль повинний мати всеохоплюючий характер.4. Учень повинен бути не тільки об'єктом педагогічних впливів учителів, але й активним суб'єктом навчально-виховного процесу.

5. Ефективність навчальної роботи учнів залежить від розвитку в них здатності до навчання, здатності розумно і правильно учитися. Для цього вони повинні опанувати загальнонавчальні уміння і навички. Тому оволодіння загальнонавчальними уміннями і навичками повинне бути включене в навчальні програми вчителів по кожному навчальному предметі.6. Навчання повинне проводитися так, щоб воно в максимальному ступені сприяло вихованню кожного учня як високоморальної, творчо-активної і соціально зрілої особистості. 7. Ефективність навчання, характер відносини учня до навчальної роботи залежать і від того, яке життя учня в школі і класі, чи задовольняє це життя його потреби й особливо потреба в емоційному насиченні, з якими почуттями він йде в школу, які емоції і почуття викликає в нього навчально-виховний процес.8. Взаємини між вчителями й учнями повинні бути засновані на оптимістичному відношенні вчителя до кожного учня: учитель повинен вірити в можливості і сили учня. Він повинний виявляти кращі і сильні сторони кожного учня і, спираючись на них, разом з учнем бороти з його слабкими якостями.

Практичні заходи щодо запобігання прогалин в знаннях учнів. Для вчителів: Вчити прийомам навчальної діяльності. Щоб засвоїти прочитане потрібно використовувати такі раціональні прийоми смислової обробки: групування матеріалу, виділення опорних пунктів, складання плану, тез, логічної схеми прочитаного, формування головної думки.2. Якщо надавати учню можливість достатньо довго переживати радість від успішної діяльності, то в нього виникає потреба в цій діяльності, стійкий мотив до заняття нею. Пред'являти учню посильні вимоги. Схвалювати учня на успішне виконання нескладних завдань до тих пір, поки в школяра не з'явиться впевненість в своїх здібностях. Закріпивши це досягнення успіху поступово ускладнювати завдання.

Для батьків:1. Виховувати риси характеру вольової людини:а) написати план, де конкретно вказати чого і як збираєшся досягти;б) обов'язково виробити критерій успіху і невдач, а також форму їх реєстрації;в) підібрати вправи, які б допомагали виробляти навички саморегуляції і самовиховання.2. Розвитку розумових здібностей допоможуть ігри в шахи, шамати, доміно, розв'язок ребусів, головоломок, кросвордів.

Презентація уроків запобігання прогалин в знаннях учнів. Логарифмічна функція, її властивості та графік (вікторина)Урок систематизації та узагальнення знань по темі: «Логарифмічна функція»Систематизація і узагальнення знань про квадратні рівняння (урок-рольова гра)

Логарифмічна функція, її властивості та графікstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.font. Size

Мета:- ввести поняття логарифмічної функції,формувати вміння будувати графік логарифмічної функції, дослідити її властивості, познайомити учнів з використанням логарифмічної функції при вивченні явищ навколишнього світу;- розвивати творче мислення, математичне мовлення;- виховувати вміння працювати разом, почуття відповідальності, культуру спілкування.

Ми повинні:- розглянути поняття логарифмічної функції; навчитися будувати графік логарифмічної функції; дослідити її властивості;- познайомитися з використанням логарифмічної функції в науці, техніці та природі.

Сьогодні на уроці ми будемо говорити про такі речі:style.colorfillcolorfill.type

Актуалізація опорних знань. Залежність змінної у від змінної х називається функцією, якщо кожному значенню х відповідає єдине значення у. 2. Як називаються змінні х та у?Х- незалежна змінна, аргумент;У – залежна змінна, функція.3. Яку функцію називають оборотною?Функція f, яка має обернену, називається оборотною 1. Що називається функцією? Наведіть прикладиstyle.colorfillcolorfill.type

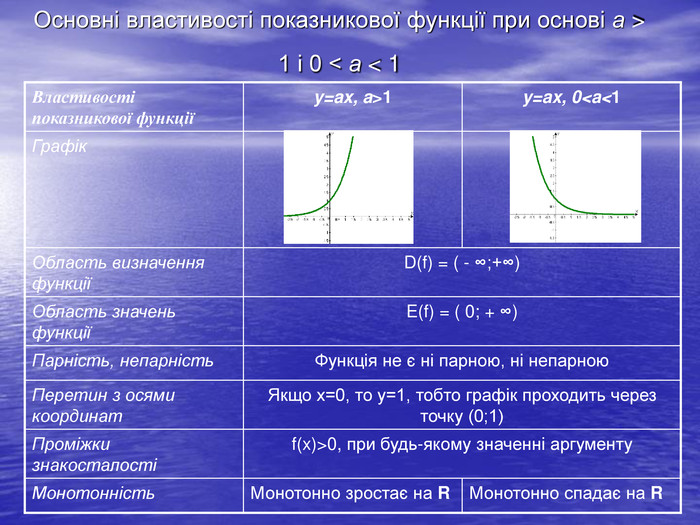
4. Назвіть достатню умову існування оберненої функції. Достатньою умовою існування оберненої функції для даної функції є її монотонність,тобто зростання або спадання на всій області визначення.5. Який існує алгоритм знаходження формули функції, оберненої до даної?а) З’ясувати, чи є функція у = f(x) оборотною на всій області визначення. Якщо ні, то виділити проміжок, на якому функціямонотонна; б) виразити х через у;в) поміняти позначення змінних 6. Накресліть схематично графіки функцій у = 3х та у = 0,5х. Сформулюйте основні властивості показникової функції при основі а > 1 і 0 < а < 1.

Основні властивості показникової функції при основі а > 1 і 0 < а < 1 Властивості показникової функції y=ax, a>1y=ax, 00, при будь-якому значенні аргументу Монотонність. Монотонно зростає на RМонотонно спадає на Rstyle.colorfillcolorfill.type

7. Сформулюйте основні властивості взаємно обернених функційа) Область визначення функції f співпадає з областю значень функції , і навпаки, область значень функції f співпадає з областю визначення функції ;б) якщо функція f зростає то і функція  зростає, якщо функція f спадає то і функція  спадає;в) графіки функції , оберненої до функції f, симетричні графіку f відносно прямої у = х8. Дайте означення логарифма і сформулюйте його основні властивості Логарифмом числа N за основою а (a>0 і a1) називається показник степеня х, до якого треба піднести а, щоб дістати N.style.colorfillcolorfill.typestyle.colorfillcolorfill.type

Поняття логарифмічної функціїМонотонна на всій області визначення. D(f) = ( - ∞ ;+ ∞), E(f) = ( 0; + ∞ )За достатньою умовою існування оберненої функціїf(x) = ax – оборотна функція. Показникова функціяf(x) = ax, a>0, a 1, a>0, a1логарифмічна функція

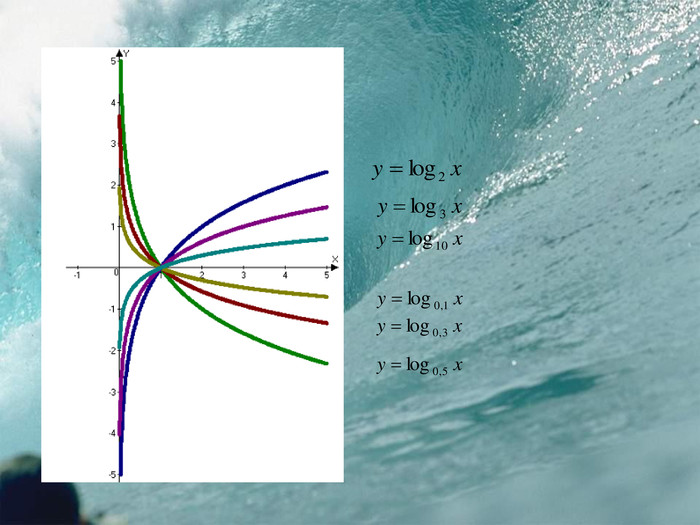
Завдання 1. За допомогою програмного педагогічного засобу Advanced Grapher побудувати в одній системі координат графіки функцій: Проблемне питання: Як можна порівнювати логарифми чисел, використовуючи властивості логарифмічної функції? Розгляньте завдання:1. Порівняйте число а з 1, якщо А. а=1. Б. а<1. В. а>1. Г. а1.2. Порівняйте числа log25 і log27. А. log25 > log27. Б. log25 < log27. В. log25 = log27. Г. log25  log27.3. Порівняйте числа log78 і log58. А. log78  log58. Б. log78 > log58. В. log78 = log58.. Г. log78 < log58.4. Порівняйте числа log4320 і log5500.style.colorfillcolorfill.type

Застосування логарифмів та логарифмічної функції в науці, техніці та природі. Математика. Логарифм – з грецької означає “логос”- відношення і “аритмос”- число. Його винахід пов’язаний з двома постатями: швейцарцем Іобстом Бюргі(1552-1632), знаним годинникарем і майстром майстром астрономічних інструментів, і шотландцем Джоном Непером (1550-1617), який теж не був математиком за професією, астрономія була його «хобі».

Логарифмічна спіраль – це крива, яка перетинає всі кути, що виходять із однієї точки О, під одним і тим же кутом α. Характерні особливості логарифмічної спіралі: Має нескінченну кількість витків як при розкручуванні так і при скручуванні;Не проходить через свій полюс;Її називають рівнокутною спіраллю;В будь-якій точці спіралі кут між дотичною до неї та її радіус-вектором зберігає постійне значення;При різних перетвореннях (гомотетії, повороті) вона залишається незмінною. Має широке застосування в технічних приладах. Властивості цієї кривої так вразили Якоба Бернуллі, що він назвав її spira mirabilis (чудова спіраль) і заповів зобразити її на його могилі з написом Eatemmutata resurgo (перетворювана, відроджуюся знову).

Фізика Робота, яку виконує газ при ізотермічному процесі:Ємність циліндричного конденсатора:Ємність дільниці одиничної довжини двох провідної лінії: Зв’язок між сталою розпаду , середнім часом життя а періодом піврозпаду Т

У гідротехніці по логарифмічній спіралі вигинають трубу, що підводить потік води до турбіни. Завдяки такій формі труби втрати енергії при зміні напряму течії в трубі виявляються мінімальними і напір води використовується з максимальною продуктивністю. Якщо літак буде летіти, дотримуючись весь час одного курсу, тобто перетинаючи всі меридіани під одним і тим самим кутом, то його шлях зобразиться на карті логарифмічною спіраллю.

Хімія. Водневий показник - це від'ємний десятковийлогарифм концентрації йонів Гідрогенур. Н= - lg С( Н+)Показник р. Н в біологічних розчинах. Рідинар. НРідинар. НШлунковий сік1,4 Сеча6,0 Сік лимона2,1 Слина,молоко7,4-8 Сік яблук "Антонівка"2,5 Слиз7,0 Томатний сік4,1 Кров7,4

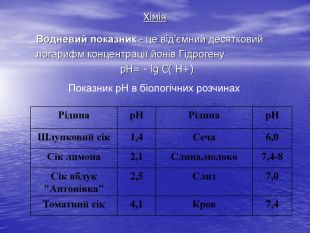
Використовуючи різні засоби особистої гігієни, креми для шкіри, ліки, необхідно враховувати значення р. Н. Більшість рідких косметичних засобів має р. Н 5,5. Відповідний вміст у них катіонів Н+ оптимальний для нашої шкіри. У сільському господарстві кислотність грунтового розчину є одним із головних чинників, що впливають на врожай. Так, картопля найкраще росте на слабокислих грунтах (р. Н≈5), а буряк на нейтральних (р. Н≈7).

Біологія Спіраль є математичним символом співвідношенняформи і зростання. Логарифмічна функція виникає у зв'язку з найрізноманітнішими природними формами. По логарифмічних спіралях розташовуються квітки в суцвіттях соняшника, закручуються раковини молюска Nautilus, роги гірського барана і дзьоби папуг. Один з павуків, епейра, сплітаючи павутиння , закручує нитки навколо центра по логарифмічним спіралям.

Нічні метелики, які пролітають величезні відстані, орієнтуючись по паралельним промінням місяця, інстинктивно зберігають прямий кут між напрямом руху і променем світла. Якщо вони орієнтуються на точкове джерело світла, інстинкт їх підводить, і метелики потрапляють в полум’я по логарифмічної спіралі, що скручується.

Музика Піфагор був не тільки великим математиком, а й хорошим музикантом. Він встановив, що приємні сполучення звуків відповідають певним співвідношенням між довжинами струн, що коливаються, або відстаням між дірочками сопілки. Саме він створив першу математичну теорію музики, і хоча музиканти не дуже люблять перевіряти „алгеброю гармонію”, вони весь час мають справу з математикою, бо сучасна гама ґрунтується на логарифмах.log2 Nmp= m + Звідси видно, що номери клавіш рояля являють собою логарифми кількості коливань відповідних звуків. Номер октави – характеристика ( тобто ціла частина) логарифма, а номер звука в даній октаві - його мантиса ( тобто дробова частина).

Яка функція є оберненою до показникової?Яка функція називається логарифмічною?При якій умові логарифмічна функція є зростаючою (спадною)?Де використовується в навколишньому світі логарифмічна функція?

Бажаємо вам успіхів у вивченні математики!!!

Урок систематизації та узагальнення знань по темі: «Логарифмічна функція»

Мета:узагальнити та систематизувати знання учнів по темі “Логарифмічна функція”, формувати вміння застосовувати вивчений матеріал до розв’язування задач практичного змісту, підготуватися до тематичної контрольної роботи.розвивати логічне мислення, обчислювальні навики, математичну мову учнів, вміння спостерігати навколишні явища, виховувати любов та інтерес до математики.

Організаційний момент

ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ З історичних джерел Перші зародки поняття логарифма можна знайти в Архімеда, але сама ідея розвитку не набула. Триста років тому в епоху Відродження почався бурхливий розвиток науки, техніки і мореплавства. Розвиток астрономії, а точніше астрономічних спостережень, вимагали нових методів обчислень, які були б доступні широкому колу людей. В основу таких методів і були покладені логарифми.

Для обчислення логарифмів довгий час використовували логарифмічну лінійку, яку сконструював англійський математик, священик Оутред в 17 ст. Близько 350 років вона залишалася надійним апаратом для наближених, але швидких обчислень. Але час іде, наука і техніка рухаються вперед, і на зміну логарифмічній лінійці прийшов мікрокалькулятор.

Ода логарифму  Різноманітні застосування показникової і логарифмічної функцій надихнули англійського поета Елмера Брілла на написання „Оди експоненті". Були поети, які не присвячували од логарифмам, але згадували їх в своїх віршах. У вірші „Фізики і лірики" Борис Слуцький написав: Потому-то, словно пена, Опадают наши рифмы. И величие степенно Отступает в логарифмы.

Гра «Найрозумніша команда» 1 9 223 16 6 7 810 2 21 185 11 4 12 17 13 14 15 19 20

Перший учень: Знайти область визначення функції: y = lg x - 2/3x - 9. Другий учень: Розв'язати рівняння: lg2x - lg + 1 = 0. Третій учень: Схематично зобразити графік функції: y = log2(x-2).

Робота в парах:1. Знайти область визначення функції: y = 5/ log3 (x+2).2. Розв'язати нерівність: а) log 1/3 (x-1) > 2; б) log5 (2x-4) < log5 (x+1).

Узагальнення та повторення раніше здобутих знань (практикум). а) для групи слабких учнів;б) для групи змішаного типу;в) для групи сильних учнів;

Захист робіт

Усі учні одержують оцінки незалежно від того, як пройшов захист робіт і враховуючи фронтальне повторення. 121110987654321

Домашнє завдання:

Розв'язати: Знайти Д(у) функції y = 7/log4(x+5).2. Розв´язати нерівності:а) log ½ (x+1) < 2;б) log 0,3 ( - x - 2) > log 0,3 (10-2x).3. Розв'язати рівняння:а) 2 log2 (-x) = 1 + log (x+4);б) 2 log5 x + log 0,2 x = 2.4. Додаткові вправи до уроку (збірник завдань для екзамену з математики).

Дякуюза урок)

Систематизація і узагальнення знань про квадратні рівняння (урок-рольова гра)Слава Тобі, Господи,що ти створив усе потрібне простим,а все складне – непотрібним. Григорій Сковорода

Мета. Систематизація і узагальнення знань про квадратні рівняння. Розвиток пізнавальних інтересів. Виховання логічної грамотності

Рівняння в авангарді науки Без рівнянь немає математики як засобу пізнавання природи (виступ істориків)Джеймс Максвел теоретично довів існування електромагнітних хвиль. “Важко повірити, що ці математичні формули живуть незалежним життям і навіть мають власний інтелект, що вони мудріші за нас самих”. Поль Дірак 1923 рік квантове рівняння руху електрона. Дослідження якого пояснює низку явищ мікросвіту (аномалії магнітного моменту, процеси анігіляції, електронно-позитронне поле, існування частинок і античастинок... )Томсон, скориставшись теорією Фурє, розвязав “телеграфне рівняння” і “зєднав” металевою ниткою Америку та Європу. Рівняння стало поштовхом до відкриття закону Ома.

Історична справка. Багато вчених, починаючи з Евкліда й аль-Хорезмі, збагачували науку способами розв’язуваня різних рівнянь. Серед них: Франсуа Вієт “Усі математики знали, що під алгеброю сховано незрівнянні скарби, але не могли їх знайти. Задачі, які вони вважали найбільш складними, дуже легко можна розвязати десятками за допомогою нашого мистецтва”. Омар Хайям . Він був мудрою людиною, обізнаною в усіх галузях філософії, а надто математики. Його праця ”Про доведення задач і алмукабали” містить теорію розвзування рівнянь. «Я тільки знаю, що знання шукаю, В найглибші таємниці проникаю. Я думаю вже сімдесят два роки – І бачу, що нічого я не знаю.»

Актуалізація опорних знань(повторити за підручником)Знати означення таких понять: Рівняння. Корінь рівняння. Розвязати рівняння. Рівносильні рівняння. Рівносильні перетворення

Перевір себе. Рівність із змінною f(x ) =  (x) називається рівнянням з однією змінною х. Будь-яке значення змінної при якому вирази f(x ) і  (x) приймають рівні числові значення, називають коренем рівняння. Розвязати рівняння - означає знайти всі його корені або довести, що їх нема. Рівняння, що мають одні й ті самі корені, називаються рівносильними. Рівносильними вважаються також рівняння, кожне з яких не має коренів. Якщо в рівнянні перенести доданок з однієї частини в другу, змінивши його знак, то дістанемо тотожне рівняння f(x)+ g(x) =  (x) + g(x); якщо обидві частини рівняння помножити або поділити на одне й те саме відмінне від нуля число, то дістанемо рівняння, рівне даному f(x)·g(x) =  (x)·g(x).

Квадратним рівнянням, називається рівняння виду αх²+bх+с=о, де х – невідоме, α, b, с – деякі числа, α≠0. Числа α, b, с – коефіцієнти квадратного рівняння. α – перший коефіцієнт, b – другий коефіцієнт, с – вільний член. Якщо α =1, рівняння називається зведеним, Якщо хоча б один із коефіцієнтів b або с дорівнює 0, рівняння називається неповним. Щоб з рівняннями дружити Потрібно формули вчити.

Способи розв’язування рівнянь(виступ теоретиків)Якщо а+b+c =0, то х1 =1, х2 = с/а. Якщо а-b+c =0, то х1 =-1, х2= - с/а. Якщо b = 0 і с = 0 , то αх² = 0 і має один корінь х = 0. Якщо с = 0, b≠0, то αх²+ bх =о; х(αх +b)=о; х1=0; х2 = - b/а. Якщо с≠0, b = 0, αх²+ с =о, то х1,2 =± √-с/а, якщо –с/а < 0, рівняння коренів не має. Розв’язування через дискримінант D = b² – 4ac, то х1,2 = (-b±√ D) / 2a.7. Якщо D > 0 - рівняння має два корені ; якщо D = 0, рівняння має один корінь; якщо D<0, рівняння коренів не має.8. Теорема Вієта х1 + х2 = -b /а ; х1•х2 = с/а, Для зведеного рівняння x²+ px +q = 0 : x1+x2 =-p та x1•x2=q; якщо q<0 x1 і x2 мають різні знаки, якщо q>0 x1 і x2 обидва від’ємні чи обидва додатні. Знак x1 і x2 є протилежним до знака p.10. Виділення повного квадрата.

Початкове усвідомлення знань(виступ практиків)1. 1999х² – 1997х – 2 =0 а+b+c =0  1999 – 1997 – 2 = 0, отже х1 =1, х2 = - 2/ 1999.2. 1999х ² + 1997х – 2 = 0 Так як 1999 – 2 = 1997  х1 = - 1 , х2 = 2/1999. Усно розв’яжи рівняння:5х ² – 11х + 6 = 0; 3х ² – 5х + 2 = 0; х ² – 6х – 7 = 0; 2а ² + а – 3 =0; х ² + 4х +3 = 0.3. 5х ² = 0  х= 04. 2х ² – 7х = 0  х(2х – 7 ) = 0, х1 =0, х2 = - 3, 5.5. 3х ² + 27 = 0 3х ² – 27 = 0х ² = -9 х ² = 9рівняння не має коренів х1,2 = ± 3.6. Розглянемо випадок, коли другий коефіцієнт – парне число.ах ² + 2kх +с = 0, D = (2k) ² – 4ac = 4k2 – 4ac = 4(k ² – ac ), нехай D1 = k ² –ac, якщо D1 > 0, то x1,2 = (- k ± D1) / a; якщо D1 = 0, то x = - k/a;якщо D1 < 0, то дійсних коренів не має. Наприклад: 3х ² – 10х + 7 = 0, D1 = (-5)2 - 3•7 = 25 – 21 = 4 = 22 > 0; х1,2 = (5±2)/3, х1 = 2⅓, х2 = 1.7. Вказати, яка з пар чисел буде розв’язком квадратного рівняння (усно). а) х ² +5х – 500 = 0. А. -20; 25. Б. 20; -25. В. -20; -25; Г. 20; 25. б) t ² – 8t +12 = 0. А. 2; 6. Б. 3; 4. В. -2; 6. Г. -2; -6. в) х ² – 5х – 500 = 0. А. -20; 25. Б. 20; -25. В. -20; -25; Г. 20; 25.8. 3х ² – 5х – 2 = 0, перейдимо до зведенного вигляду, для цого поділемо коефцієнти рівняння на 3, маємо х ² – (5/3) х – 2/3 = 0, або х ² – 2•(5/6)х – 2/3 = 0 , отримаємо повний квадрат х ² - 2•(5/6)• х + (5/6)2 – (5/6)2 – 2/3 = 0, (х – 5/6 )2 = 25/36 + 24/36, (х – 5/6 )2 = 49/36, х – 5/6 = 7/6 або х – 5/6 = -7/6 х = 2 або х = - 1/3.

Тренувальні вправи. Робота 1. Квадратні рівняння

Робота 2. Зведене квадратне рівняння. Учні самостійно розв’язують три рівняння, а отримані результати заносять до таблиці: Використовуючи результати формулюємо теорему Вієта.

Робота 3. Фронтальна робота(клас поділений на рівномірні за знаннями групи, в кожній з яких є історики, теоретики і практики)1. Які знаки коренів рівняння?а) х ² – 15х + 4 = 0; б) х ² +7х +10 = 0; в) х ² + 6х – 7 = 0; 2. Розв’язати квадратні рівняння:а) 5х ² – 8х + 3 = 0; б) х ² + 2х – 3 = 0; в) 5х ² + 8х + 3 = 0; г) х ² – 2х – 3 = 0;Знайти значення виразу а+b+c для рівнянь а) та б). Знайти значення виразу а- b+c для рівнянь в) та г).3. Використовуючи зроблені висновки, розв’яжіть рівняння: 17х ² – 15х – 2 = 0; 71х ² + 75 +4 = 0.

Робота 4. Обернена до теореми Вієта

Різнорівневі карточки. Картка – інструктор

Картка – інструктаж. Розв’яжи рівняння 7/х + (21 – 63х) / 7 + 8х – 9 = 0 Зведи до спільного знаменника, враховуючи, що знаменник не дорівнює нулю;Розкрий дужки;Зведи подібні доданки;Отримай зведене квадратне рівняння (а=1);Знайди дискримінант;Обчисли корені;Запиши відповідь.

Висновок: Рівняння – це не просто рівність. З однією змінною чи кількома. Рівняння – це думок активність, Це інтелекту боротьба. То ж будьте творчими, активно розвивайтесь, Долайте труднощі у своєму житті, Але з рівняннями, прошу, не розлучайтесь, Вони послужать вам ще в майбутті.

МАТЕМАТИЧНЕМОДЕЛЮВАННЯ

Моделювання – одна з основних категорій теорії пізнання. На ідеї моделювання базується будь-який метод наукового дослідження.

Що таке моделювання? Це метод пізнання, який полягає у створенні та дослідженні моделей.

Що таке модель? Це спеціально створений об’єкт, який відображує суттєві особливості досліджуваного об’єкта, явища або процесу.

Моделі бувають Фізичні Математичні

Метод фізичного моделювання. Полягає у створенні лабораторної фізичної моделі явища у зменшеному масштабі і проведення експериментів на цій моделі. Висновки і результати, одержані на моделі, розповсюджуються на явище в реальних масштабах

Приклади фізичних моделейзменшені моделі літакаавтомобіля будівліЗемної кулі

Математичними моделями є: Вирази Геометричні фігури Формули Функції Рівняння Нерівності Системи рівнянь Системи нерівностейstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Якими математичними поняттями зручно змоделювати предмети з навколишнього середовища

Математика тісно пов’язана з життям. Математичними методами розв’язують не тільки абстрактні математичні задачі про числа, фігури, рівняння, нерівності, функції, системи рівнянь та нерівностей, а й багато інших.

Задачі, які виникли поза математикою, але розв’язуються математичними методами, називаютьсяприкладними

Це задачі, взяті з. Фізики. ХіміїЕкономіки. БіологіїЕкологіїЖиттєвих ситуаційstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Як розв’язувати прикладну задачу?1) Ознайомитися з повною умовою задачіСтворити математичну модель до неї, тобто здійснити переклад з природної мови на математичну3) Провести розрахунки. Сформувати відповідь5) Порівняти отримані результати з нормоюstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Реальні процеси та явища мають кількісні, тобто числові показники. А кожна абстрактна задача є математичною моделлю деякої прикладної задачі

Тому девізом уроку є вислів М.І. Лобачевського"Все в природіповинно бути виміряно,все може бути пораховано"

Розв’язування прикладних задач

Задача 1. Скільки дошок потрібно, щоб настелити підлогу в кімнаті довжиною 7,5 м і шириною 5 м, якщо довжина дошки 6 м, а ширина 0,25 м?

Задача 2. Водопровідний кран погано закритий. За 6 хвилин набігає повна склянка води. Скільки води витече з такого крана за 1 годину, якщо в 1 літрі міститься 5 склянок води?

Задача 3. Сім’я з трьох чоловік на добу потребує 51 кг чистого повітря. Скільки кг повітря потрібно на наш клас?

Задача 4. Корова прив’язана на галявині до кілка мотузкою завдовжки 8 м. Яку площу вона випасає?

Задача 5. Катер за 4 год. пройшов 24 км за течією річки і 20 км – проти течії. Знайти швидкість течії, якщо власна швидкість катера дорівнює 12 км/год.

Задача 6. 30%-ий розчин борної кислоти змішали з 15%-вим і отримали 400 г 20%-го розчину. Скільки грамів кожного розчину було узято?

Задача 7. Визначити життєву ємність легенів (ЖЄЛ), якщо дихальний об’єм (ДО) становить 400 мл, резервний об’єм вдиху (РО вд) – 2000 мл, а резервний об’єм видиху (РО вид) – 1500 мл.

Моделювання як метод наукового пізнання застосовується в багатьох інших сферах, наприклад:style.colorfillcolorfill.typestyle.colorfillcolorfill.type

Моделювання зачісок

Моделювання одягу. Шкільна форма

Моделювання у педагогіці

Урок закінчено. ДОПОБАЧЕННЯ!