Презентація "Прямі у просторі"

ПРЯМІ У ПРОСТОРІЕлектронний навчальний посібник з геометрії

Розміщення прямих у просторіПодорож по темі

Як здійснити подорож?Мапа для подорожі Виберіть потрібну вам зупинку і клік миші на ній, щоб повернутися до мапи скористайтесь кнопкою. Для переходу між слайдами 1 клік миші, якщо є кнопка не нехтуйте нею. Переглянути теоретичнапобутовамалюнковаперевірочнавідпочивальна

Зупинка “ТЕОРЕТИЧНА”На цій зупинці ви можете дізнатися, яким чином розміщуються прямі у просторі.style.font. Family

Дві пряміЛежать в одній площиніНе лежать в одній площині (мимобіжні)Мають спільну точку (перетинаються)Не мають спільних точок (паралельні)Взаємне розміщення прямих у просторі

ba b. Зображення і позначення:nmlpnmlp. IIa. Прямі перетинаються. Прямі паралельніПрямі мимобіжні

Дві прямі в просторі називаються паралельними, якщо вони:1) лежать в одній площині2) не перетинаютьсяab Означення Переглянути (1) Паралельні прямі

aba. IIbс. Прямі а і с не паралельніПереглянути (2) Прямі b і с не паралельні

Дві паралельні прямі визначають площину(означення паралельних прямих)ab. Переглянути (1)

Два відрізки називаються паралельними, якщо вони лежать на паралельних прямих.ab Означення. АВСDАВ II СDmn. FLFL II n. Переглянути (2)Відрізок FL паралельний прямій n. Відрізки АВ и СD паралельні

А Через точку, що не лежить на даній прямій, проходить тільки одна пряма, паралельна даній. Повторення. ПЛАНІМЕТРІЯ. аb. Аксіома паралельності.

Теорема. Через будь - яку точку простору, що не належить даній прямій можна провести пряму паралельну даній і до того ж тільки одну. Мab. Пряма і точка, що не належить їй, визначають площину. Переглянути (2)Повторити ПЛАНІМЕТРІЯ

Наслідок з аксіоми паралельності. аcb. Якщо пряма перетинає одну з двох паралельних прямих, то вона перетинає і іншу. a. IIb, c b c a. Повторення. ПЛАНІМЕТРІЯ.

Лемма Якщо одна з двох паралельних прямих перетинає площину, то і інша пряма перетинає цю площину. МПереглянути (1)ab. КПовторити ПЛАНІМЕТРІЯ

аbс. Наслідок з аксіоми паралельності. Якщо дві прямі паралельні третій, то вони паралельні a. IIс, b. IIс a. IIb. Повторення. ПЛАНІМЕТРІЯ.

abс Ознака паралельності прямих. Якщо дві прямі паралельні третій, то вони паралельні між собою. КПовторити ПЛАНІМЕТРІЯstyle.text. Decoration. Underline

Означення. Дві прямі в просторі називаються мимобіжними, якщо вони не лежать в одній. Мимобіжні прямі

Якщо одна пряма лежить в даній площині, а друга пряма перетинає цю площину в точці, що не належить першій прямій, то ці прямі мимобіжні. Ознака мимобіжних прямихstyle.font. Size

А чи зустрічаємо ми ці види прямих в побуті?Зупинка “Побутова ”

Оаbcde a,b,c,d,e: прямі, що перетинаються

style.colorfillcolorfill.type

Паралельні пряміПрямі, що перетинаються. Мимобіжні прямі

Зупинка “Малюнкова”На цій зупинці спробуйте з'ясувати розміщення прямих у просторі за допомогою малюнків

AB1 A1 PCBDD1 MNKC1 Задача 1 Дано: ABCDA1 B1 C1 D1 – КУБ. K, M, N – СЕРЕДИНИ РЕБЕР B1 C1, D1 D, D1 C1 ВІДПОВІДНО, P – ТОЧКА ПЕРЕТИНУ ДІАГОНАЛЕЙ ГРАНЕЙ AA1 B1 B. ВИЗНАЧТЕ ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХstyle.colorfillcolorfill.type

AB1 A1 PCBDD1 MNKC1мимобіжні№ 1

AB1 A1 PCBDD1 MNKC1№ 2перетинаються

AB1 A1 PCBDD1 MNKC1№ 3паралельні

AB1 A1 PCBDD1 MNKC1№ 4мимобіжні

AB1 A1 PCBDD1 MNKC1№ 5перетинаютьсяppt_xxshearppt_x

ABPMNCSKЗадача 2 Дано: SABC - ТЕТРАЙДР. ТОЧКИ K, M, N, P – СЕРЕДИНИ РЕБЕР SA, SC, AB, BC ВІДПОВІДНО. ВИЗНАЧТЕ ВЗАЄМНЕ РОЗМІЩЕННЯ ПРЯМИХstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

ABPMNCSK№ 1 Паралельні

ABPMNCSK№ 2 Мимобіжні stroke.colorstroke.onppt_xxshearppt_x

ABPMNCSK№ 3 Перетинаються

ABPMNCSK№ 4 Перетинаютьсяstroke.colorstroke.on

Куди поїхати?Зупинка “перевірочна”На цій зупинці ви зможете перевірити свої знання з темиstyle.colorfillcolorfill.typefill.on

Перевір себеаааbbb. Назвіть взаємне розміщення прямих.перетинаютьсямимобіжніпаралельніstyle.colorfillcolorstroke.colorfill.type

Відповідь: Мимобіжні. Як в просторі розміщені прямі EH і FG?Завдання 1

В тетраедрі ABCD назвіть пари мимобіжних ребер. Відповідь: AB і CD; BC і AD; AC і BD. Завдання 2

Відповідь: A1 D1; B1 C1; DD1; CC1. Дано куб A…D1. назвіть прямі, що проходять через вершини цього куба і мимобіжні до прямої AB. Завдання 3

Розв'язок: Кожне ребро бере участь в чотирьох парах мимобіжних прямих. . У куба 12 ребер. Значить , шукане число пар паралельних прямих дорівнює Скільки є пар мимобіжних прямих, які містять ребра куба A…D1? Завдання 4

Розв'язок: Кожне ребро бере участь у 8 парах мимобіжних прямих. Кожне бічне ребро приймає участь у 8 парах мимобіжних прямих. Значить, шукане число пар мимобіжних прямих дорівнює Відповідь : Завдання 5 Скільки є пар мимобіжних прямих, які містять ребра правильної шестикутної призми?

№ 1 QАСВDNMPТочки М, N, P і Q – середини відрізків BD, CD, AB і АС. РMNQP - ?12 см14 см

Перевірка (3) Прямі, що містять сторони АВ і ВС паралелограма АВСD перетинаються в площині α. Доведіть,що прямі AD і DC також перетинають цю площину. САОDЯке взаємне розміщення точок О, Р, М, N?РМNВ№ 2

Дано: АА1 II СС1, АА1 II ВВ1, ВВ1 = СС1 Довести, що В1 С1 = ВСАВ1 СА1 ВС1 Перевірка № 3

Дано: А1 С1 = АС, А1 С1 II АС, А1 В1 = АВ, А1 В1 II АВ Довести, що CС1 = ВB1 АВ1 СА1 ВС1 Перевірка№ 4

АВСЕFKM Трикутник АВС і квадрат АEFC не лежать в одній площині. Точки К і М – середини відрізків АВ и ВС відповідно. Доведіть, що КМ II EF. Знайдіть КМ, якщо АЕ=8см.8см№ 5

АВССDKM Квадрат АВСD і трапеція KMNL не лежать в одній площині. Точки A і D – середини відрізків KM і NL відповідно. Доведіть, що КL II BC. Знайдіть BC, якщо KL=10см, MN= 6 см. NL10см6 см№ 6

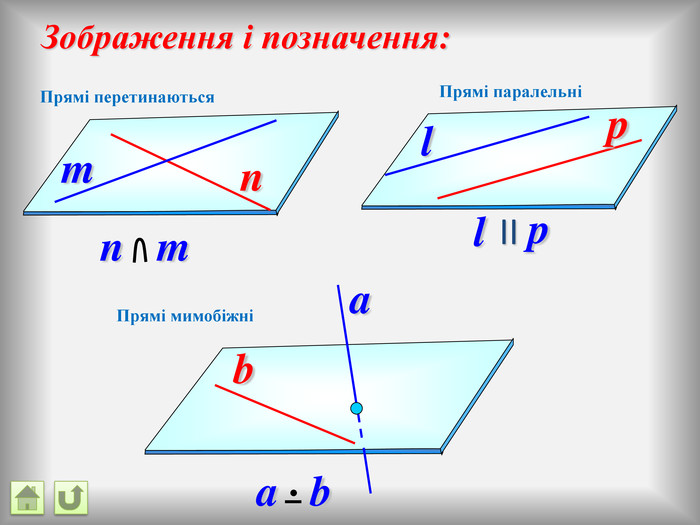
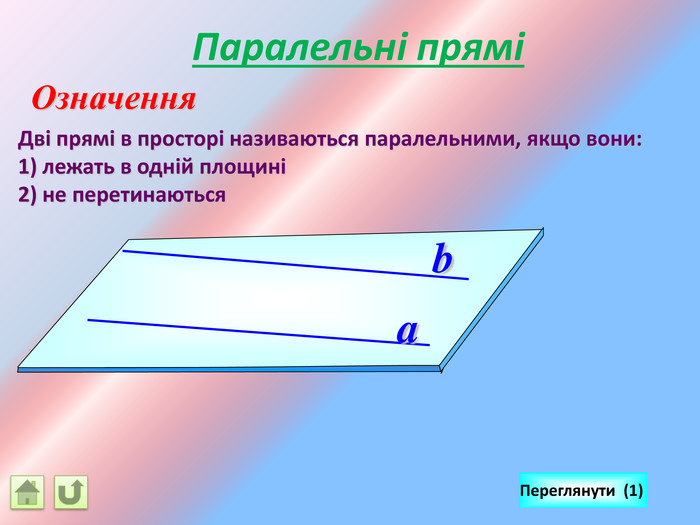
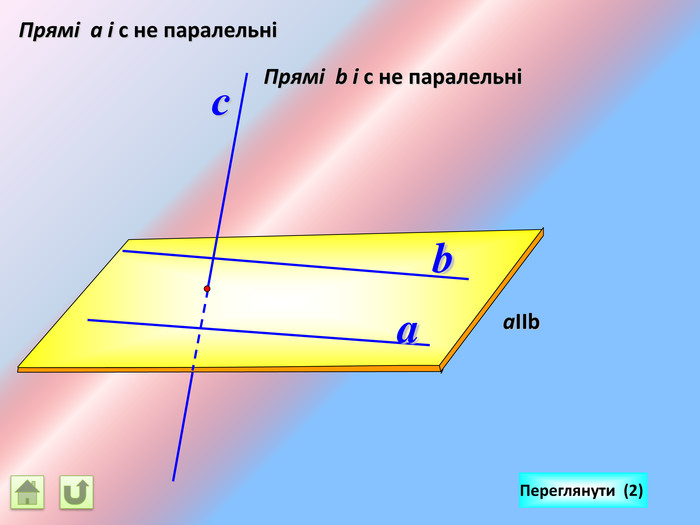
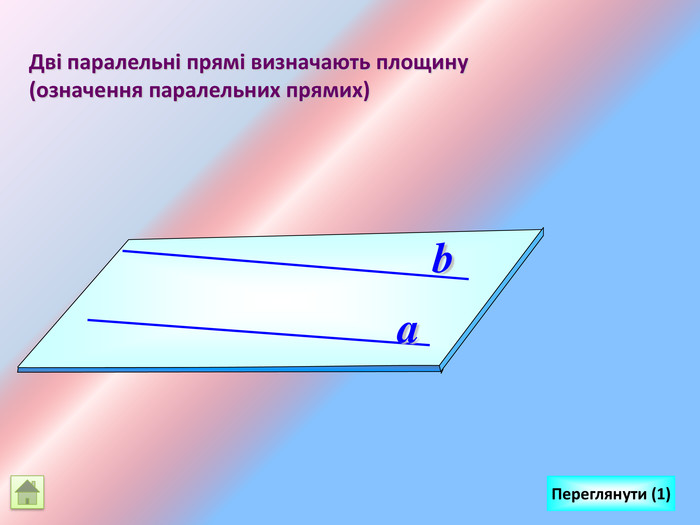
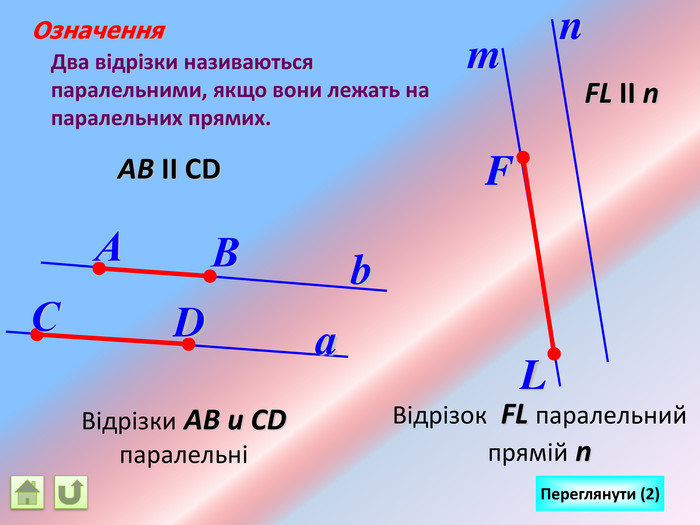
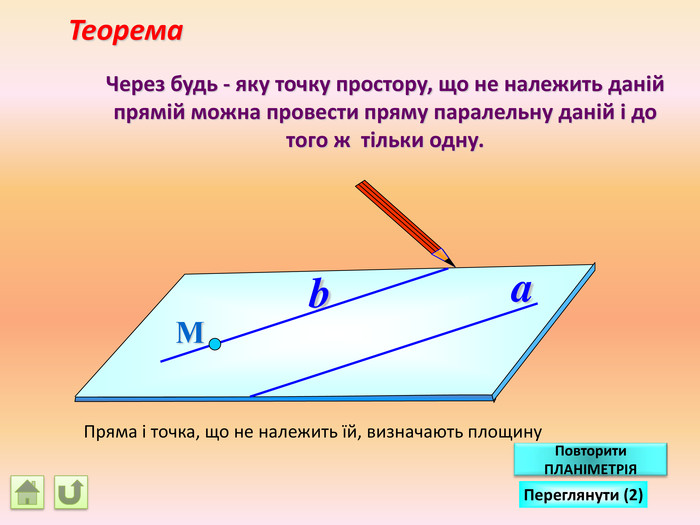
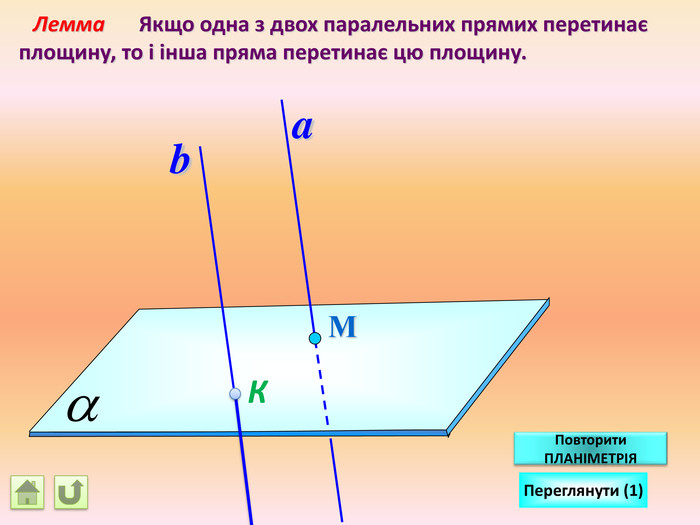
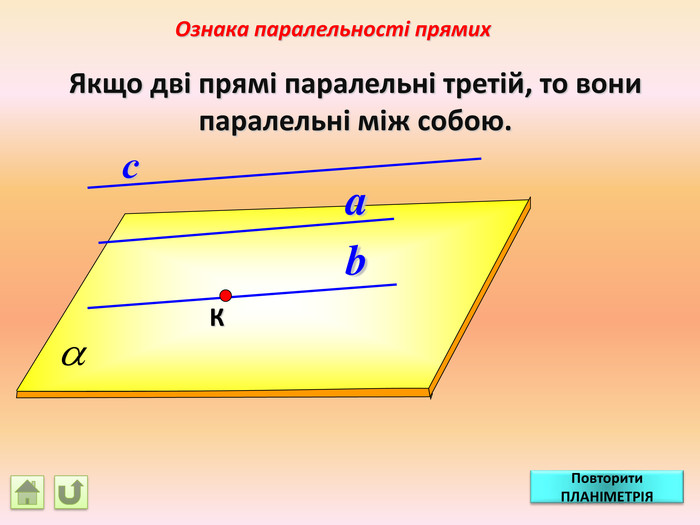
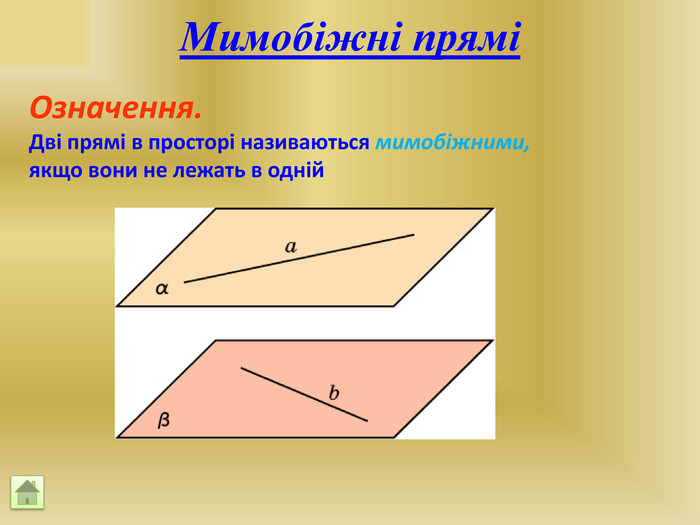
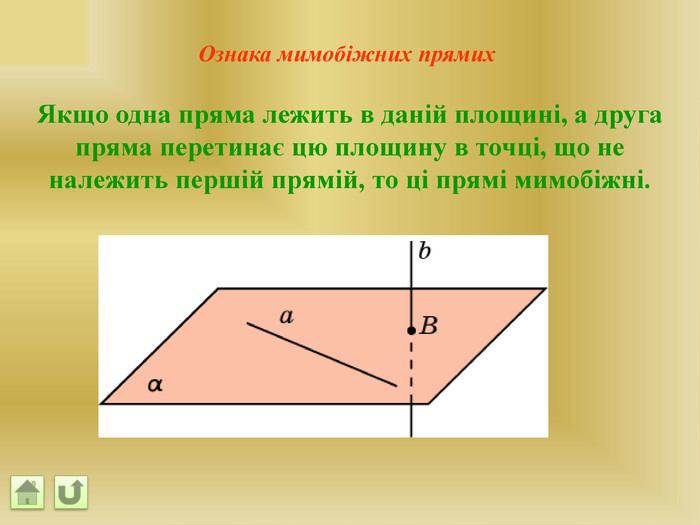
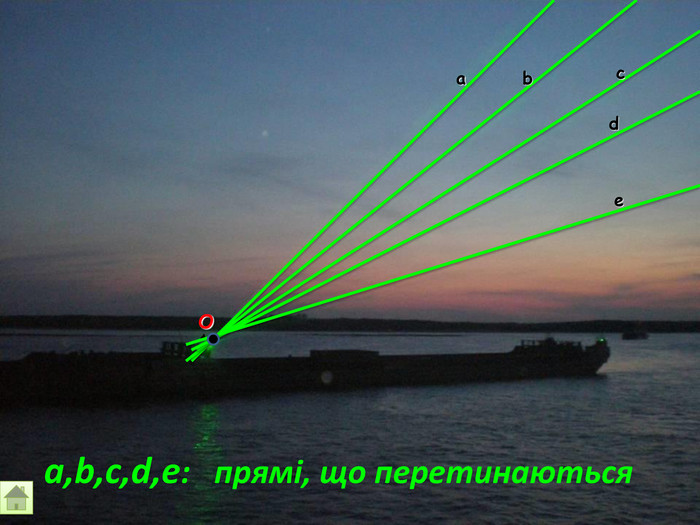
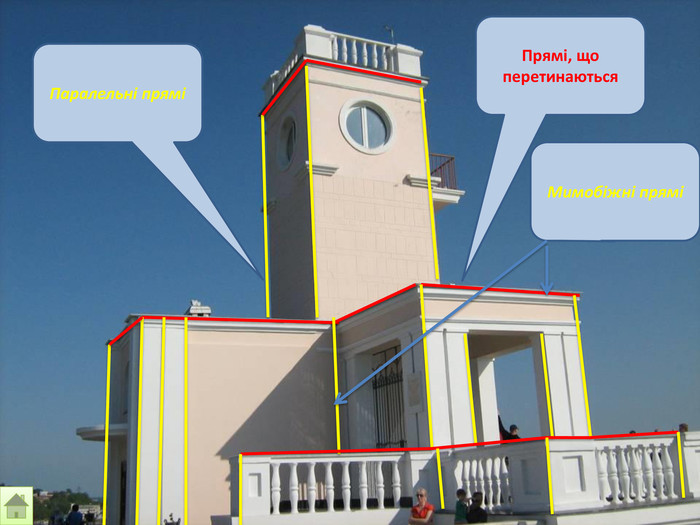
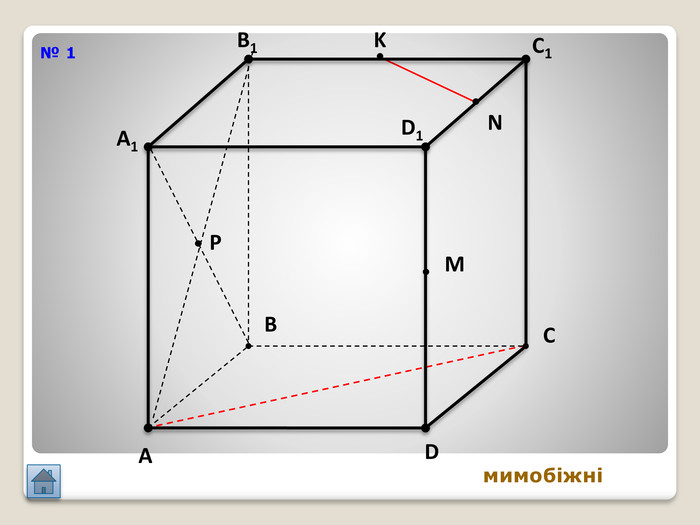
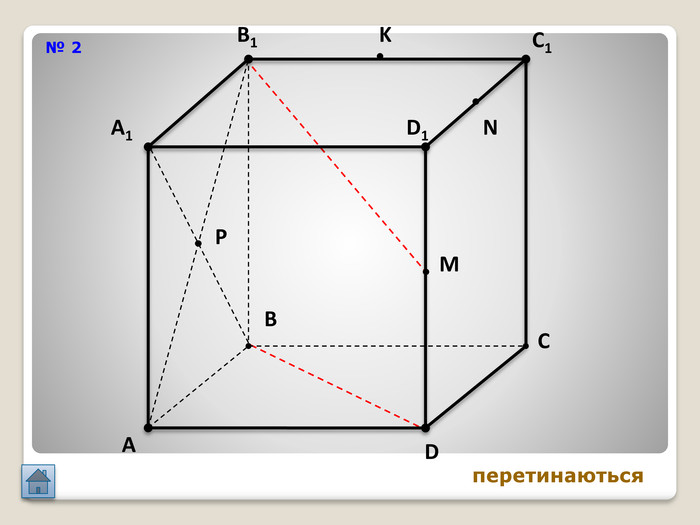
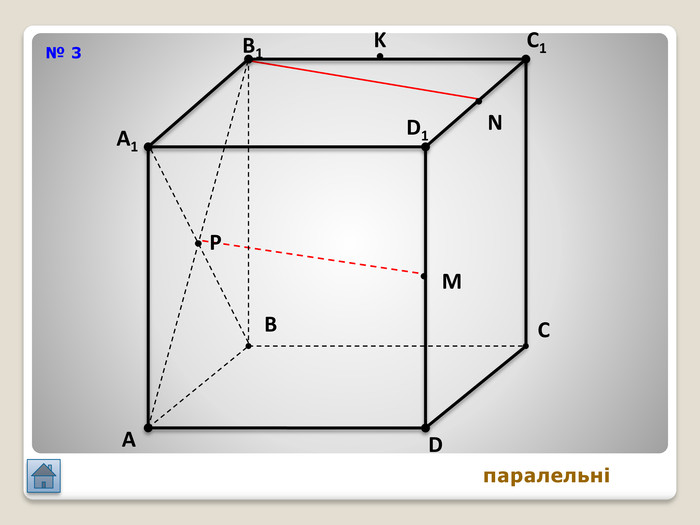
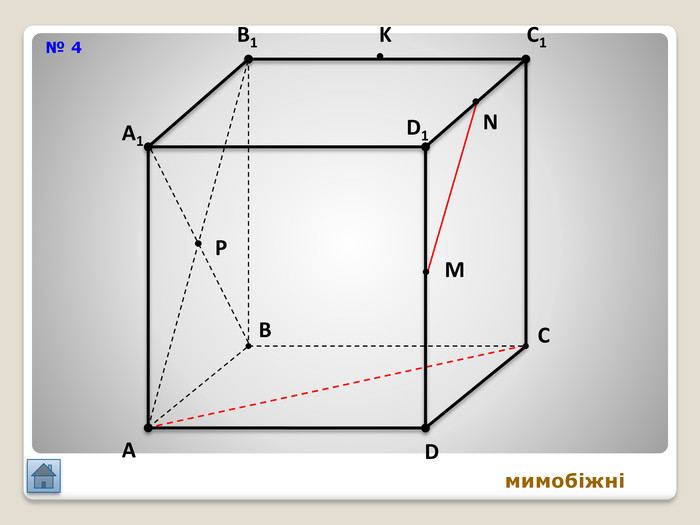
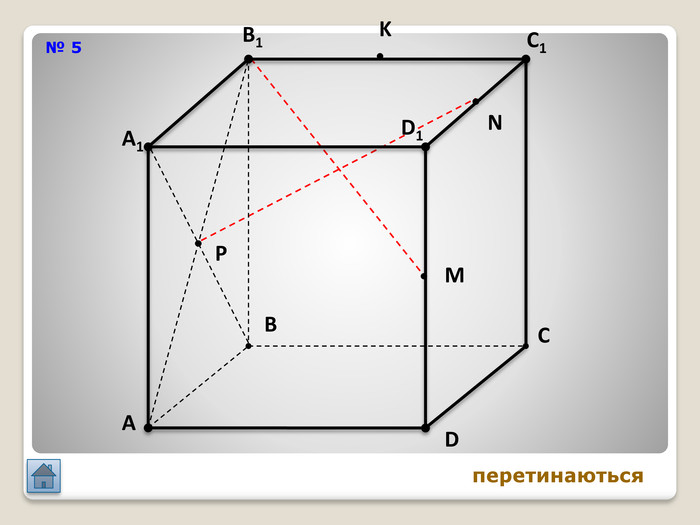
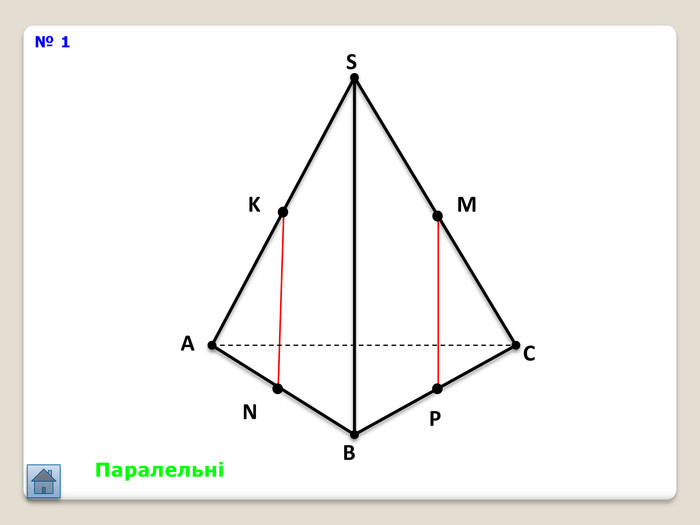
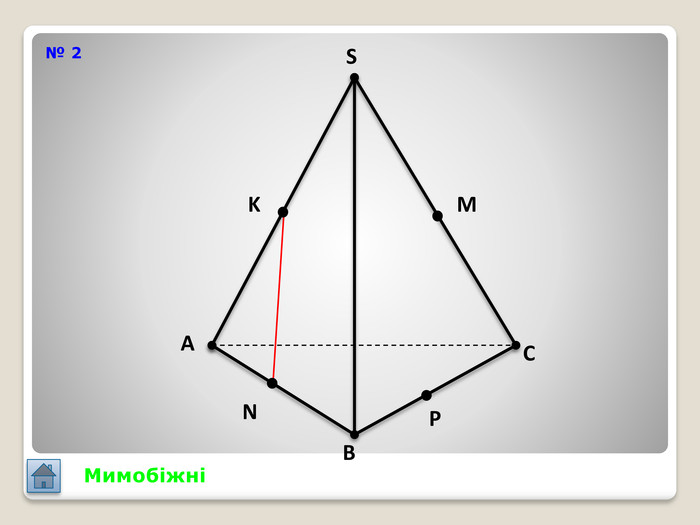
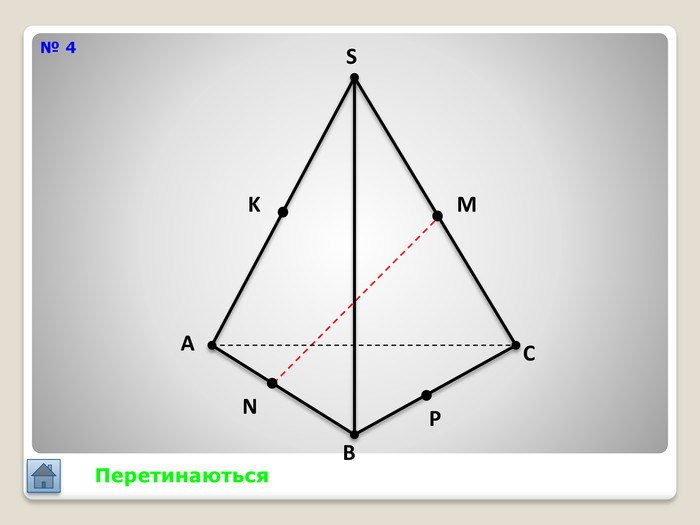
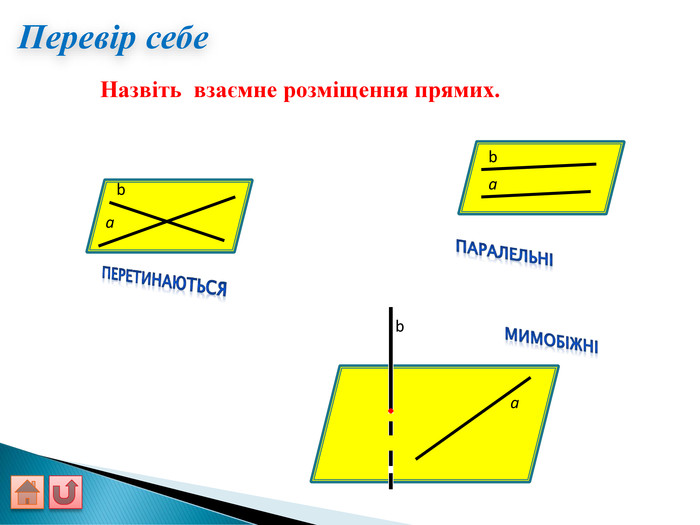
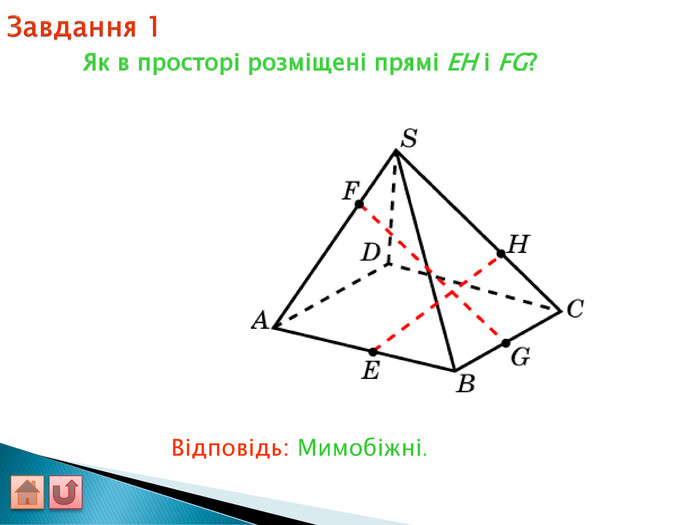
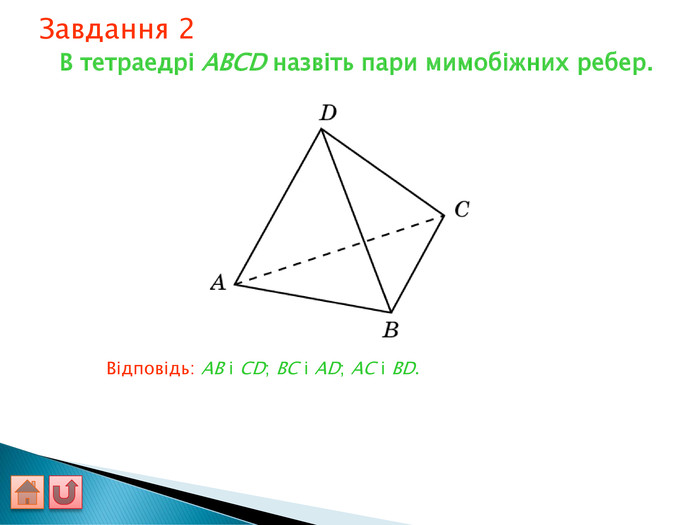
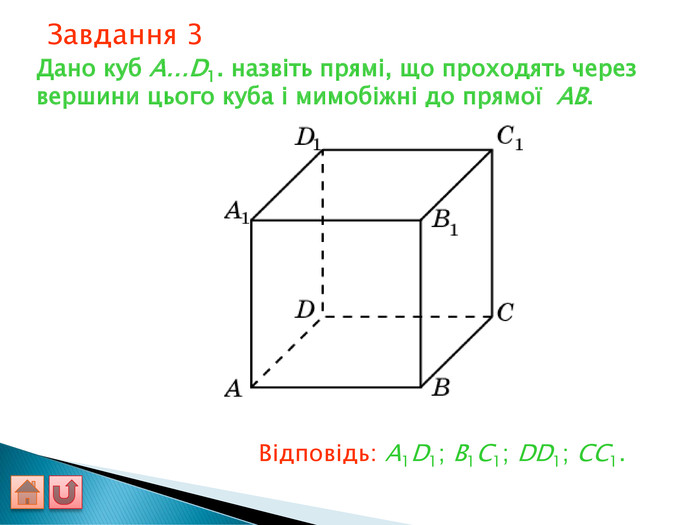
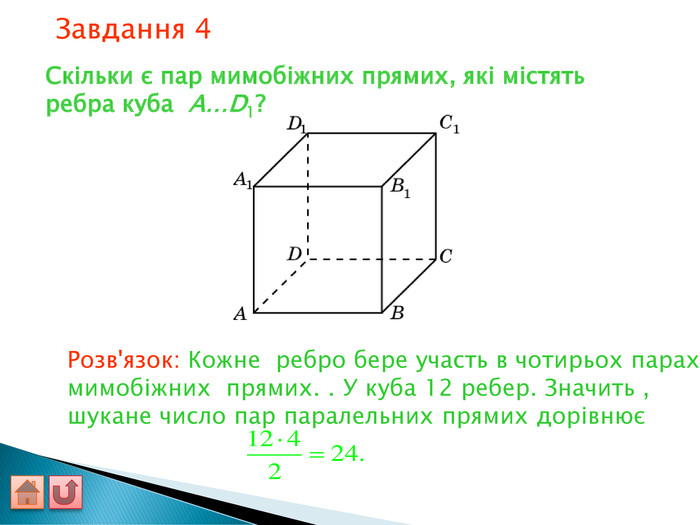
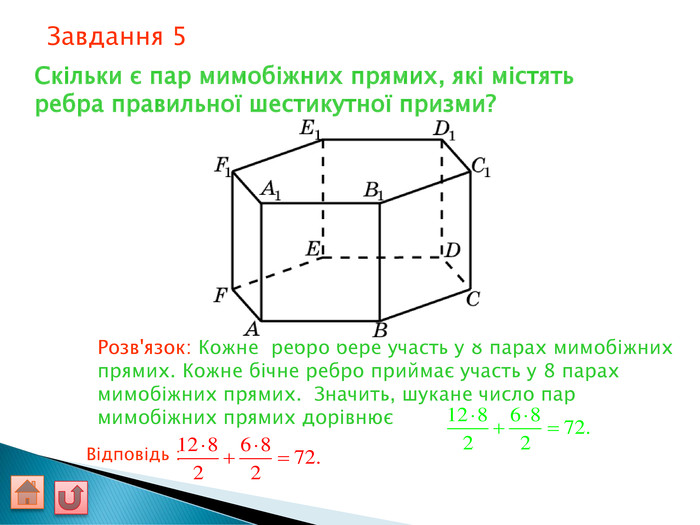
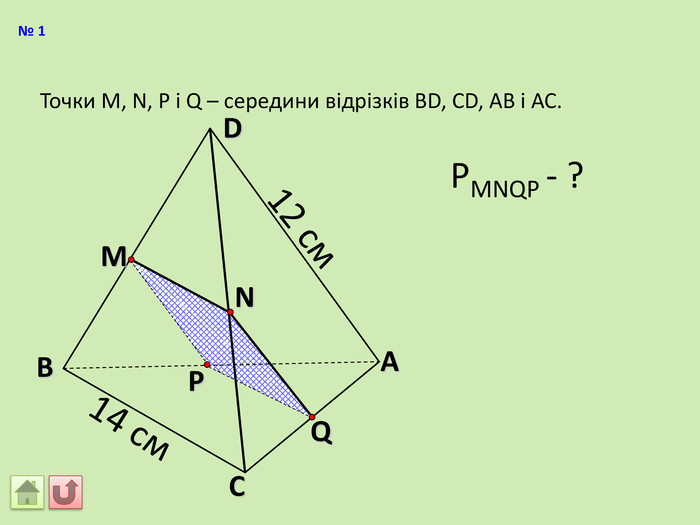
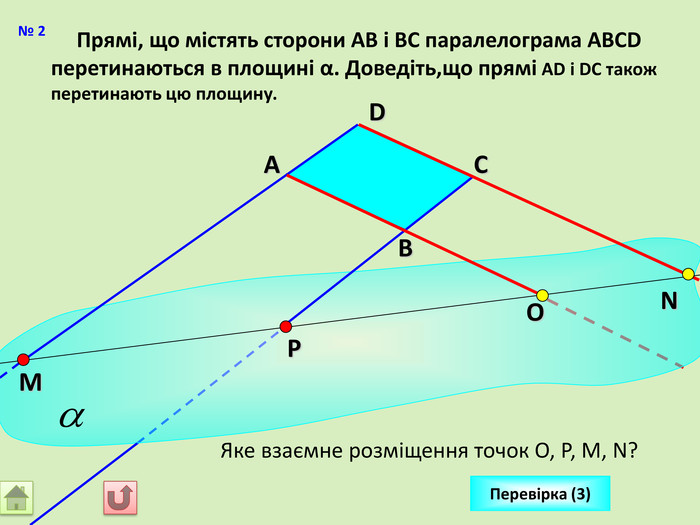
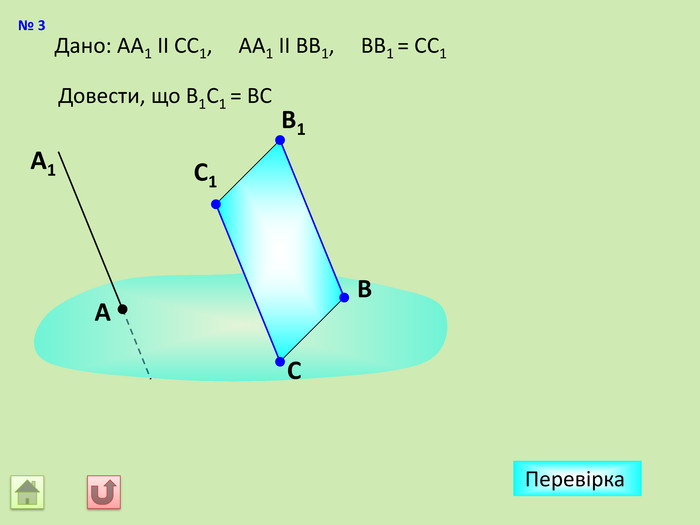
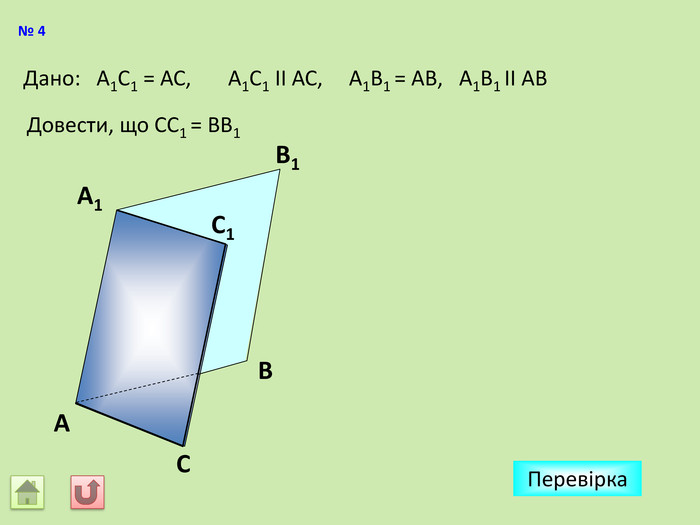
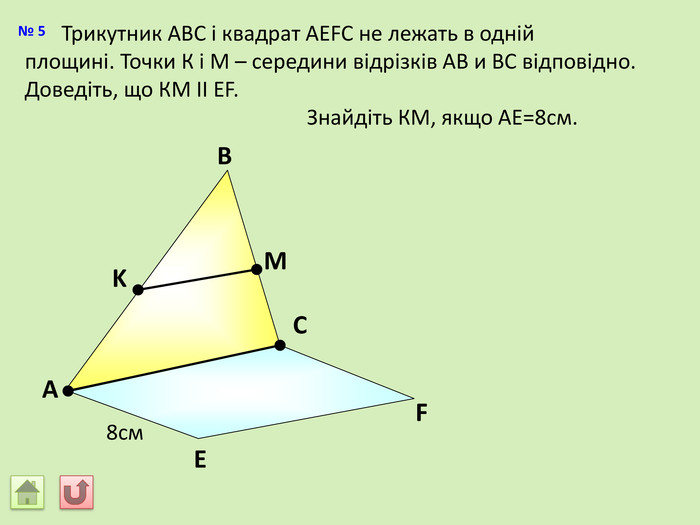
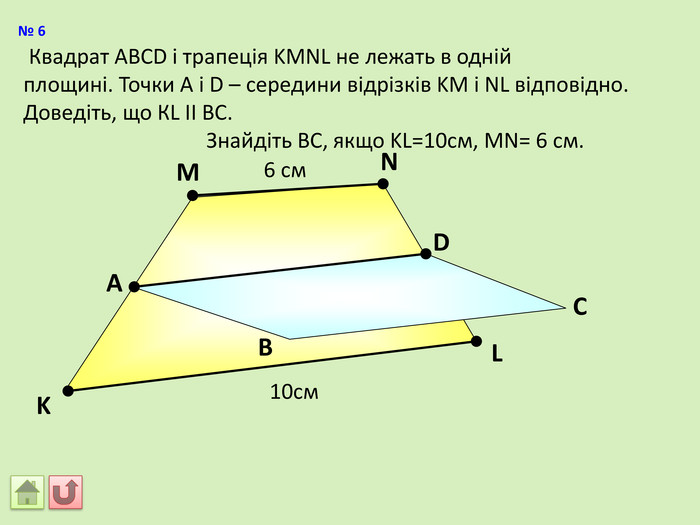
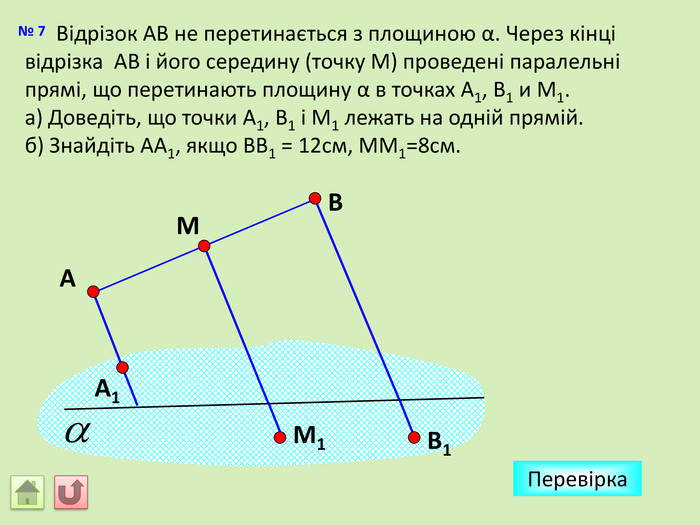
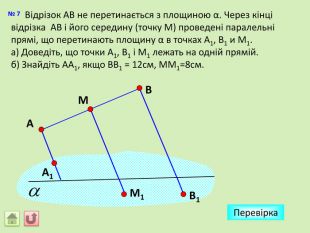
Відрізок АВ не перетинається з площиною α. Через кінці відрізка АВ і його середину (точку М) проведені паралельні прямі, що перетинають площину α в точках А1, В1 и М1. а) Доведіть, що точки А1, В1 і М1 лежать на одній прямій. б) Знайдіть АА1, якщо ВВ1 = 12см, ММ1=8см. АМВПеревірка. В1 А1 M1№ 7

Зупинка “Відпочивальна”style.colorfillcolorstroke.colorfill.type

Олівці Чи можливе таке розміщення олівців?

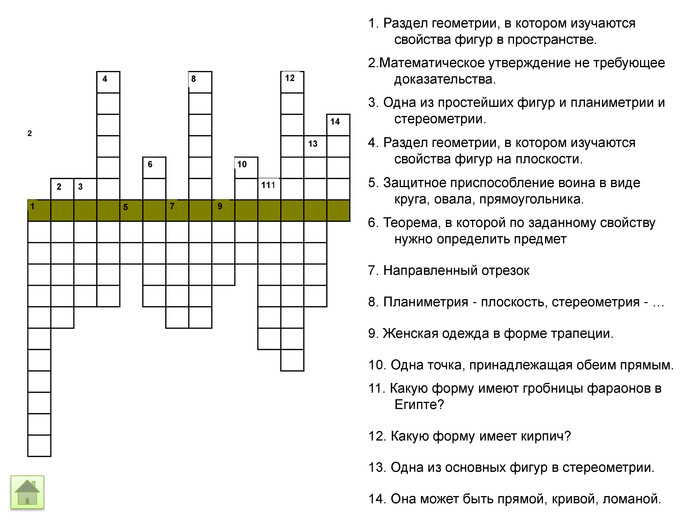
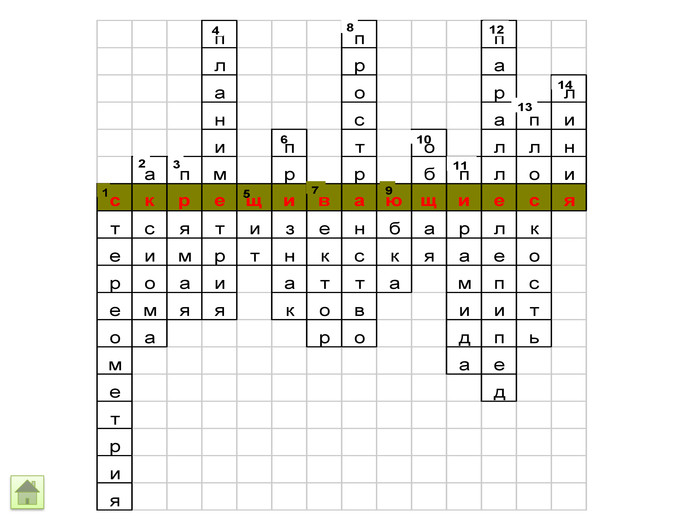
21. Раздел геометрии, в котором изучаются свойства фигур в пространстве.2. Математическое утверждение не требующее доказательства. 3. Одна из простейших фигур и планиметрии и стереометрии.4. Раздел геометрии, в котором изучаются свойства фигур на плоскости.5. Защитное приспособление воина в виде круга, овала, прямоугольника.6. Теорема, в которой по заданному свойству нужно определить предмет7. Направленный отрезок8. Планиметрия - плоскость, стереометрия - …9. Женская одежда в форме трапеции.10. Одна точка, принадлежащая обеим прямым.11. Какую форму имеют гробницы фараонов в Египте?12. Какую форму имеет кирпич?13. Одна из основных фигур в стереометрии.14. Она может быть прямой, кривой, ломаной.

Ромб

паралелограм