Основний зміст теми «Чотирикутники» на уроках геометрії

Комунальний заклад «Нікопольська середня

загальноосвітня школа I-III ступенів № 25 з поглибленим

трудовим і профільним навчанням»

 

 

 

Основний зміст теми «Чотирикутники»

на уроках геометрії

 

 

 

 

                                                                                                   Підготувала:

учитель математики

Калєйнік Юлія Микoлаївна

 

 

 

 

 

 

                                                       2018 p.

Основний зміст теми: “Чотирикутники”

Розв’язанням однієї з важливих задач загальноосвітньої і професійної школи є посилення прикладної спрямованості навчання. У зв’язку з цим важливо виробити в учнів уміння при вирішенні конкретних питань орієнтуватися на істотні властивості об’єктів і явищ.  Великі можливості для формування такого вміння має вивчення теми “Чотирикутники”.

Запропонований матеріал представляє великі можливості для організації різних форм колективної учбово-пізнавальної діяльності учнів, формування їхнього діалектико-матеріалістичного світогляду, закладає фундамент для розвитку вміння застосовувати геометричні знання при вирішенні питань життєво-практичного і виробничого характеру.

В якості провідної ідеї візьмемо ідею чіткого розмежування властивостей і ознак паралелограма і його частинних випадків.

Насамперед потрібно домогтися, щоб учні навчилися розрізняти поняття “властивість фігури” і “ознака фігури”. Якщо дано, що фігура паралелограм, і виходячи з цього доводять деякі співвідношення між елементами розглянутої фігури, то кожне з цих співвідношень називається властивістю фігури, про яку мова йде в умові теореми.

Наприклад, теорема: “У паралелограма протилежні сторони рівні, протилежні кути рівні”, коротко може бути записане так:

 

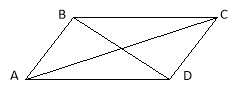
     Дано:  АВСD – паралелограм.

     Довести:   1) АВ = СD; AD = ВC;

       2) А = C; B = D.

 

Кожне зі співвідношень (1), (2) висновку теореми дає властивість паралелограма.

Більш глибокого й свідомого засвоєння понять “властивість” і “ознака” можна домогтися, якщо зв’язати їх з поняттями “необхідна умова”, “достатня умова”, “необхідна і достатня умова”.

Повідомляємо школярам, що будь-яка теорема може бути записана у вигляді АB, де А — умова теореми (що дано), а В — висновок теореми (що потрібно довести).

Якщо доведена теорема АB, то А є достатнім для В (як тільки є А, то зараз же буде й B), а В — необхідне для А, з А необхідно випливає В.

Ще більш переконливе обґрунтування того, чому умова B вважається необхідною для А, можна дати, якщо познайомити учнів з питанням про види теорем і зв’язку між ними. Записуємо схему:

(1) АВ                       BА (2)

(3) не А  не В           не В  не А (4)

Повідомляємо, що якщо твердження (1) назвати прямим, то твердження (2) буде до нього зворотним, твердження (3) — протилежним прямому, а (4) – протилежне зворотному. Далі доводиться, що зі справедливості твердження (1) випливає справедливість твердження (4) [(1)(4)] і навпаки, тобто (4)(1).

Повідомляється, що якщо (1)(4), то твердження називаються еквівалентними. Аналогічно еквівалентні твердження (2) і (3) [(2)(3)].

Словами формулу (1)(4) можна розшифрувати так: якщо з умови А слідує (випливає) умова В, то без B немає й А (з не B не А), іншими словами В необхідно для А (без B не буде й А).

А далі повідомляємо, що необхідна умова дає нам властивість, а якщо умова не тільки необхідна, але й достатня, то одержуємо ознаку.

 Іншими словами, щоб одержати властивість B якого-небудь об’єкта А, досить довести теорему АB, а щоб переконатися, що розглянута властивість B є ознакою, варто ще довести теорему ВА (зворотну).

Разом з учнями згадуємо всі властивості паралелограма і складаємо таблицю.

Дано: АВСD – паралелограм

Довести:

АВ || СD ВC || AD АВ = СD ВC = AD АO = ОС ВO = ОD

А = C B = D А + B = 1800 C + B = 1800 C + D = 1800 А + D = 1800

Звертаємо увагу на той факт, що кожна з умов 1–12 випливає з того, що АВСD — паралелограм, отже, кожна з них є необхідною умовою того, щоб чотирикутник АВСD був паралелограмом. Легко переконатися, що з кожної з умов 1–12 не випливає, що АВСD — паралелограм (наприклад, якщо дано, що АВ || СD, то маємо трапецію, тому що відрізок ВC не паралельний AD).

Таким чином, кожна з умов 1–12, взята окремо, ознакою паралелограма не є. Тепер почнемо комбінувати властивості по дві (Скільки таких комбінацій буде? Як порахувати всі комбінації, щоб бути переконаним, що жодна з них не пропущена?). Переконуємося, що деякі з комбінацій дають ознаку паралелограма. Які з комбінацій по двох дають відомі уже вам ознаки паралелограма? [(1, 2), (1, 3), (2, 4), (5, 6)].

Природно постає питання, скільки ж усього ознак у паралелограма? Для відповіді на це питання потрібно перебрати всі можливі комбінації й довести отриману теорему, або привести приклад, що спростовує її (контрприклад). Ясно, що ця робота не може бути виконана на уроці. Вона може бути дана в якості індивідуального завдання додому успішним учням, чи ще краще, запропонована в якості колективної роботи гуртківцям. Тут постають цікаві питання про планування роботи, про поділ праці при розв’язанні цієї проблеми, про організацію самоконтролю і взаємоконтролю, про підведення остаточних висновків, тобто питання, що виникають при організації будь-якої трудової діяльності.

 Тут учитель знайомить учнів зі ще одним способом одержання тверджень обернених даному. Зауважує, що умова прямої теореми може бути розбита на дві частини.

Дано: 1) АВСD — паралелограм.

2) А=90⁰.

Довести: АС = ВD.

Якщо тепер поміняти місцями висновок і другу частину умови, то ми одержимо твердження:

Дано: АВСD — паралелограм

АС=ВD.

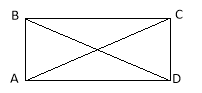Довести: А=90⁰.

Це твердження легко довести.  Доведіть самостійно.

Якщо учні затрудняються, то можна “навести” їх на думку, звернувши увагу, що А + D = 180⁰ (АВСD — паралелограм ). Що залишилося тепер довести? (А=D).

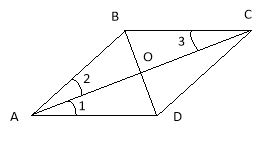Аналогічну роботу проводимо з встановленням ознак ромба, що базуються на властивостях його діагоналей. Згадуємо теорему про властивості діагоналей ромба.

Дано: АВСD — ромб.

Довести: 1) ВD АС;

2) ВАС =САD.

 

 

 

Для цієї теореми можна

скласти дві обернені:

Теорема 1                                   Теорема 2

Дано: ВD АС                           Дано: ВАС = САD

Довести: АВСD — ромб.            Довести: АВСD — ромб.

Легко показати, що кожна з цих теорем несправедлива, привівши хоча б по одному контрприкладу;

 

 

 

 

Цікаве питання. А як можна видозмінити перший рисунок щоб його можна було використовувати одночасно для спростування і теореми 1 і теореми 2? (Досить взяти АО=ОС і тоді AВD=DВС).

Використовуючи другий спосіб утворення зворотних теорем, з яким учні ознайомлені при встановленні ознаки прямокутника.

Маємо:

Пряма теорема:

Дано: АВСD -паралелограм, АВ = ВC.

Довести: ВD АС

Обернена теорема:

Дано: АВСD -паралелограм, ВD АС.

Довести: АВ=ВC

Згадуючи уточнене визначення ромба, даємо таке формулювання оберненої теореми: “Якщо в паралелограмі діагоналі перпендикулярні, то цей паралелограм — ромб”.

 Схема аналітичного міркування при відшуканні доведення цієї теореми.

 

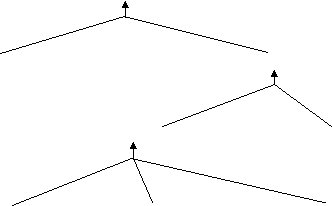АВСD – ромб

 

АВСD – паралелограм              АВ=ВC

 

АВО = СВО  АОВ = СОВ

       ВD АС

АO = ОС   BO – спільна   АОВ = СОВ

                  

АВСD – паралелограм           ВD АС

 

Доцільно підійти до розподілу диференційовано: найбільш сильним запропонувати варіант в), середнім — варіант б), іншим — а).

Задача 1. Маємо модель шарнірного чотирикутника зі сторонами визначеної довжини. Яким способами можна надати “жорсткість” даної моделі чотирикутника, якщо його вершини не можуть бути закріплені? Відповідь обґрунтувати.

В ході обговорення цієї задачі пропонуються різні варіанти її розв’язання, які перевіряються дослідним шляхом, наприклад, скріпити дві вершини чотирикутника планкою по діагоналі, з’єднати планкою середини двох протилежних сторін і т.д.

Переконавшись на досліді в розумності зроблених пропозицій, учні приходять до необхідності обґрунтувати той чи інший спосіб “надання жорсткості”. За допомогою вчителя вони приходять до можливості провести це обґрунтування, переформулювати задачу у вигляді відповідної задачі на побудову.

Можливість зведення конкретної задачі, визначеної на моделі,  до розв’язання абстрактної геометричної задачі на побудову реалізує одну з найважливіших виховних функцій геометричних задач: зв’язок навчання математиці з життям, тобто показує реальне походження математичних абстракцій.

Враховуючи “властивість жорсткості” трикутника перше з вищезгаданих розв’язань обґрунтовується досить просто. Однак обґрунтування другого шляху розв’язання задачі не настільки очевидне. Виникає вже чисто геометрична абстрактна задача.

Задача 2. Побудувати чотирикутник АВСD, знаючи довжину його сторін і довжину відрізка MN, що з’єднує середини сторін АВ і DС.

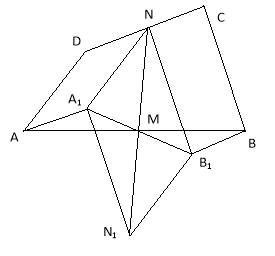Припустимо, що шуканий чотирикутник АВСD побудований. Виконаємо паралельне перенесення (DN) сторони DА і паралельне перенесення (CN) сторони СВ, тепер з точки N виходять 3 відрізка А₁N, MN, NВ₁ відомої довжини.

Неважко показати, що точка М є серединою А₁В₁. Справді, довжини відрізків АА₁ і ВВ₁ рівні 1/2DС, а самі відрізки || DС.

Тому чотирикутник А₁АВ₁В є паралелограмом. Точка М — середина його діагоналі АВ. Тому М належить діагоналі А₁В₁ і є її серединою.

Отже, у NA₁B₁ відомі сторони NA₁, B₁N і відкладена між  ними медіана. Для того, щоб побудувати цей трикутник, побудуємо точку N₁, симетрично відносно М. Очевидно,   |А₁N₁| = |В₁N|.

Трикутник N₁NA₁ можна побудувати за трьома відомими сторонами: |NA₁| = |DА|, |A₁N₁| = |В₁N| = |CB| і |NN₁| = 2|NM|.  

Тепер побудуємо шуканий чотирикутник. Ділимо відрізок N₁N  точкою М на два конгруентних відрізка, будуємо точку В₁, симетричну А₁ відносно М. За трьома сторонами будуємо трикутники А₁МА і МВВ₁.  Перенести відрізок А₁А на вектор А₁N, а відрізок ВВ₁ на вектор B₁N, отримаємо всі чотири вершини шуканого чотирикутника АВСD.

Досвід показує, що успішність в реалізації виховних функцій математичних задач багато в чому визначається пробудженням в учнів інтересу до даної задачі, виникненням у них стійкої потреби в її розв’язанні, наявністю інтересу до самого процесу розв’язання задач, на основі якого часто пробуджується і формується інтерес учнів до вивчення самої математики і суміжних навчальних дисциплін, інтерес до навчання в цілому.

Фактори, що істотно впливають на формування в учнів стійкого інтересу до розв’язання математичних задач, дуже різноманітні. До них, наприклад, відноситься доступність запропонованої задачі, зовнішня чи внутрішня цікавість задачі, усвідомлена можливість виявити при цьому творчу самостійність.