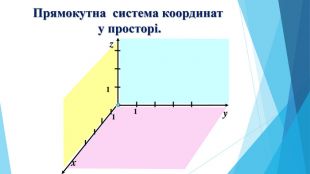
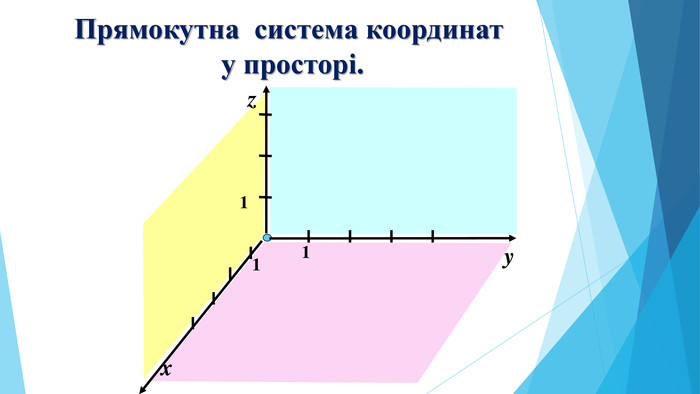
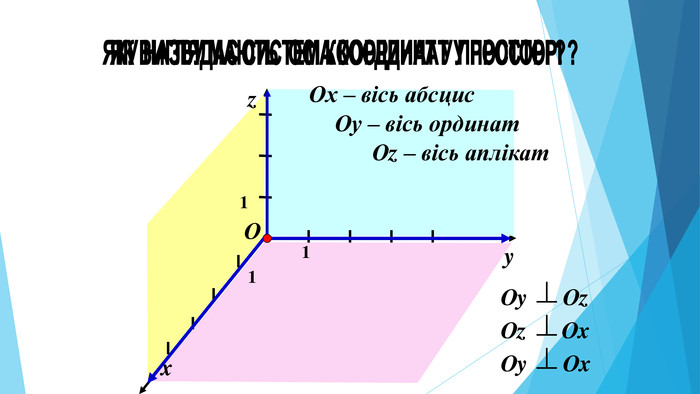
Презентація "прямокутна система координат"

Оyxz111 Прямокутна система координат у просторі.

ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ№38.6 Знайдіть відстань між точками С (6; -5; -1) і D (8; -7; 1). СD = 8−62+(−7+5)2+(1−1)2=4+4+0=8=22. №38.12 Які координати має точка, симетрична точці N (-7; 1; 0) відносно початку координат? N (7; -1; 0).№38.16 Бічні ребра прямокутного паралелепіпеда ABCDA1 B1 C1 D1 паралельні осі аплікат (рис. 38.7 на с.214), AD=3, AB=5, AA1=8. Початок координат, точка О, є серединою ребра DD1. Знайдіть координати вершин паралелепіпеда. D (0; 0; -4) D1 (0; 0; 4) C (-5; 0; -4) C1 (-5; 0; 4) B (-5; -3; -4) B1 (-5; 3; 4) A (0; -3; -4) A1 (0; -3; 4) СD = 8−62+(−7+5)2+(1+1)2=4+4+4=12=23. 

«Те, що ми знаємо — обмежено, а те, що ми не знаємо — нескінченно»П. Лаплас

РЕНЕ ДЕКАРТ (1596-1650)СТВОРИВПрямокутну систему координатІнтерактивна вправа “Мікрофон”Чому прямокутну система координат називають ще декартовою?

ЯК ВИГЛЯДАЄ СИСТЕМА КООРДИНАТ У ПРОСТОРІ ?y. Оy Оz. Оz Оx. Оy Оxx111 Оу – вісь ординат. Оz – вісь аплікат. ООх – вісь абсцисz ЯКУ НАЗВУ МАЮТЬ ОСІ КООРДИНАТ У ПРОСТОРІ ?

ЧОМУ ДОРІВНЮЮТЬ КООРДИНАТИ ТОЧКИ y. Оy Оz. Оz Оx. Оy Оxx111 Оу – вісь ординат. Оz – вісь аплікат. О (О;О;О)Ох – вісь абсцисz. О -- ПОЧАТКА КООРДИНАТ ?

Інтерактивна вправа “Знайди помилки у формулах”Відстань між двома точками А(x. А;y. А; z. А) і В(x. В;y. В;z. В) простору знаходиться за формулою АВ = (𝑥В+𝑥А)2+(𝑦В−𝑦А)2−(𝑧В− 𝑧А)2 АВ = 𝑥В−𝑥А2+𝑦В−𝑦А2+𝑧В− 𝑧А2 

Завдання 1 (ЗНО 2016) У прямокутній декартовій системі координат у просторі на осі z вибрано точку М (див. рисунок). Серед наведених варіантів укажіть можливі координати цієї точки. {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД(1;0;0)(1;1;0)(0;0;1)(0;0;-1)(0;1;0)Відповідь: В

Завдання 2 (ЗНО 2012 І сесія) Яка з наведених точок належить осі Оz прямокутної системи координат у просторі? {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГДМ(0;-3;0)N(3;0;-3)K(-3;0;0)L(-3;3;0)F(0;0;-3)Відповідь: Д

Завдання 3 (ЗНО 2012 ІІ сесія)Яка з наведених точок лежить у площині Оxz прямокутної системи координат у просторі?{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}АБВГД(0;-3;0)(0;4;-3)(3;0;-4)(-4;3;0)(-3;3;3)Відповідь: В

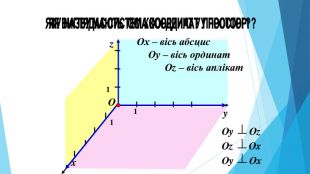
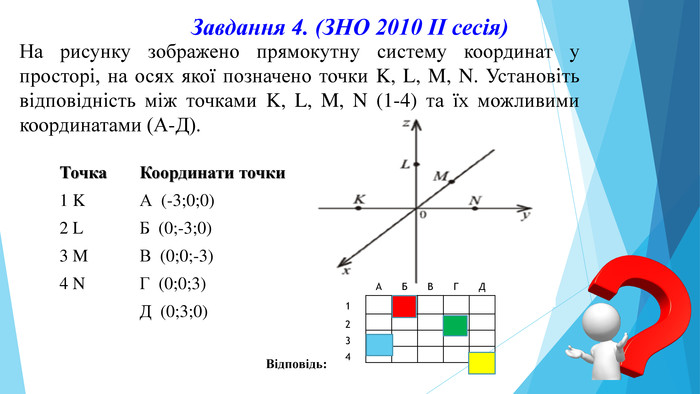
Завдання 4. (ЗНО 2010 ІІ сесія)На рисунку зображено прямокутну систему координат у просторі, на осях якої позначено точки K, L, M, N. Установіть відповідність між точками K, L, M, N (1-4) та їх можливими координатами (А-Д).{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Точка. Координати точки1 KА (-3;0;0)2 LБ (0;-3;0)3 MВ (0;0;-3)4 NГ (0;0;3) Д (0;3;0)Відповідь: {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A} АБВГД1    2    3    4    

Оyxz111 КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА. Прямокутна система координат у просторі.

ЗГААЄМОПЛАНІМЕТРІЮAВСКООРДИНАТИ СЕРЕДИНИ ВІДРІЗКАНа координатній прямій 𝒙𝑪=𝒙𝑨+𝒙𝑩𝟐    

AВхоу. СЗГАДАЄМОПЛАНІМЕТРІЮНа координатній площиніКООРДИНАТИ СЕРЕДИНИ ВІДРІЗКАА ( ) ;В ( ) ;С ( ) ;𝒙𝑪=𝒙𝑨+𝒙𝑩𝟐    𝒚𝑪=𝒚𝑨+𝒚𝑩𝟐    

У ПРОСТОРІКООРДИНАТИ СЕРЕДИНИ ВІДРІЗКАхуz. ТВЕРДЖЕННЯКОЖНА КООРДИНАТА СЕРЕДИНИ ВІДРІЗКА ДОРІВНЮЄ ПІВСУМИ ВІДПОВІДНИХ КООРДИНАТ ЙОГО КІНЦІВAВС тобто серединою відрізка з кінцями в точках А (x. А; y. А; z. А) і В (x. В; y. В; z. В) є точка С 𝒙А+𝒙В𝟐; 𝒚А+𝒚В𝟐;𝒛А+𝒛В𝟐. 

Оyxz111 РОБОТА З ПІДРУЧНИКОМ№ 38.7№ 38.17№ 38.19№ 38.20

ДОМАШНЄ ЗАВДАННЯ: Опрацювати §6 п.38; №38.8, №38.18, №38.21; підготуватися до самостійної роботи.

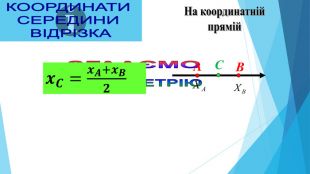
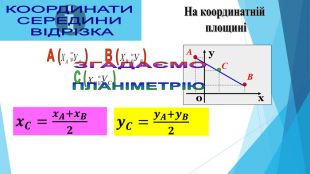
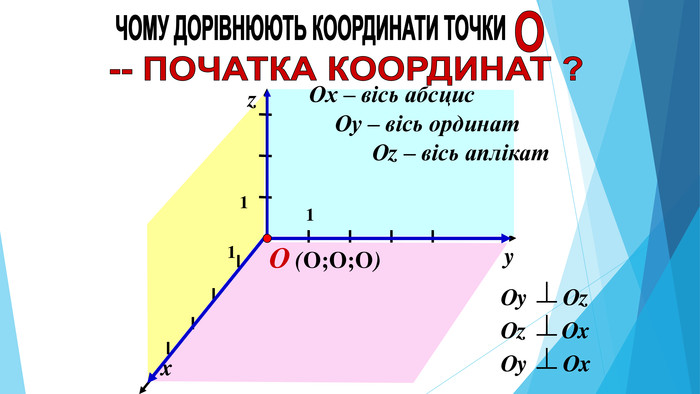
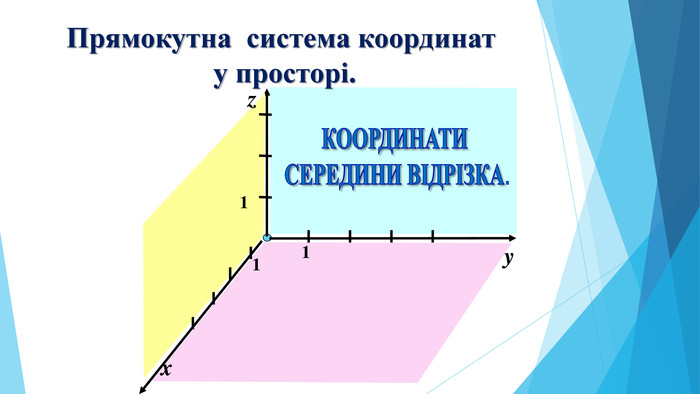
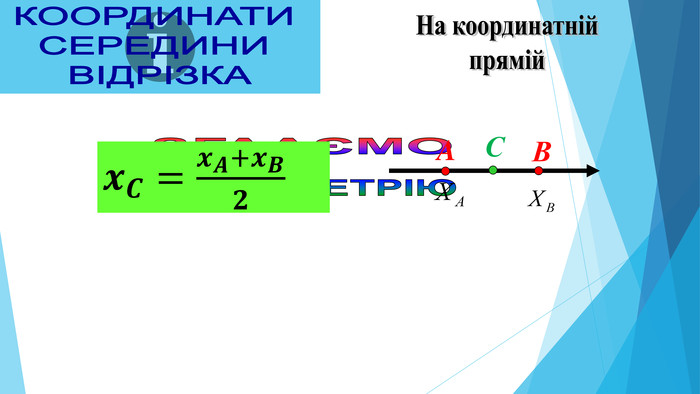
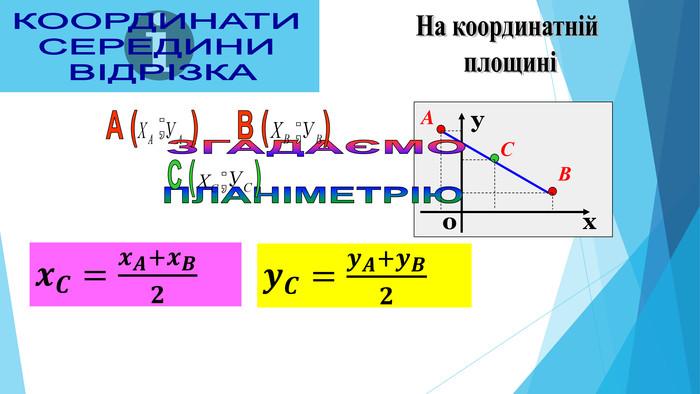
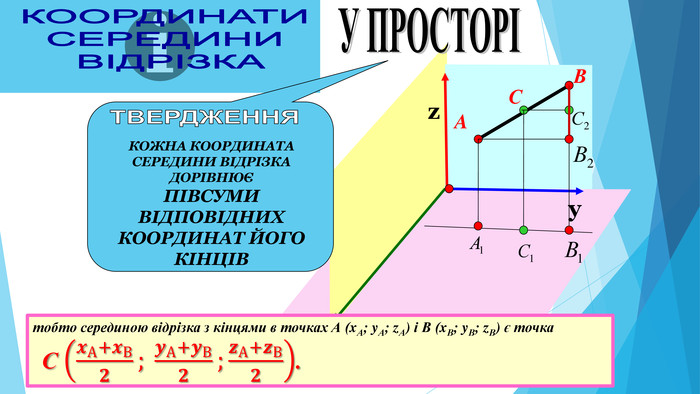
AВСНА КООРДИНАТНІЙ ПРЯМІЙКООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА AВхоу. СНА КООРДИНАТНІЙ ПЛОЩИНІУ ПРОСТОРІхуz. Координати середини відрізка,якщо точки належать координатній прямій. Координати середини відрізка,якщо точки лежать у координатній площиніКоординати середини відрізка,якщо точки лежать у просторі