Презентація "Розкладання многочленів на множники способом групування"
Про матеріал
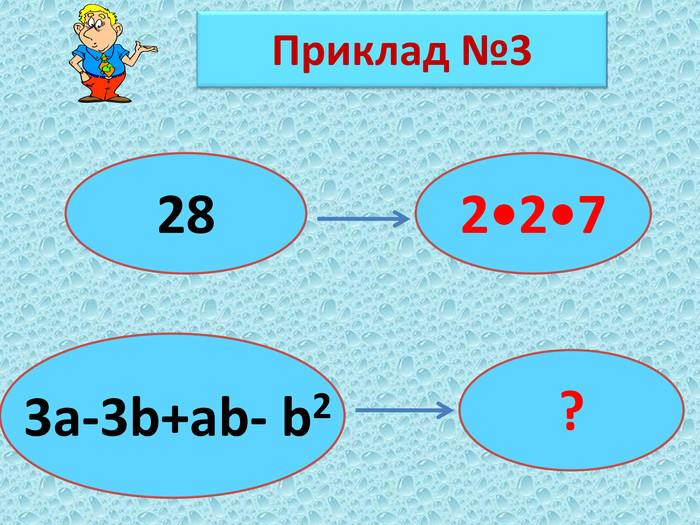
Презентація для учнів 7 класу. Передбачає ознайомлення учнів з алгоритмом розкладання многочленів на множники методом групування. Розпочато роботу із засвоєння вмінь використовувати цей алгоритм для розкладання многочленів на множники. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 7 клас (Мерзляк А.Г., Полонський В.Б., Якір М.С.)
До уроку
Метод групування Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку