Презентація Розв'язування ірраціональних рівнянь














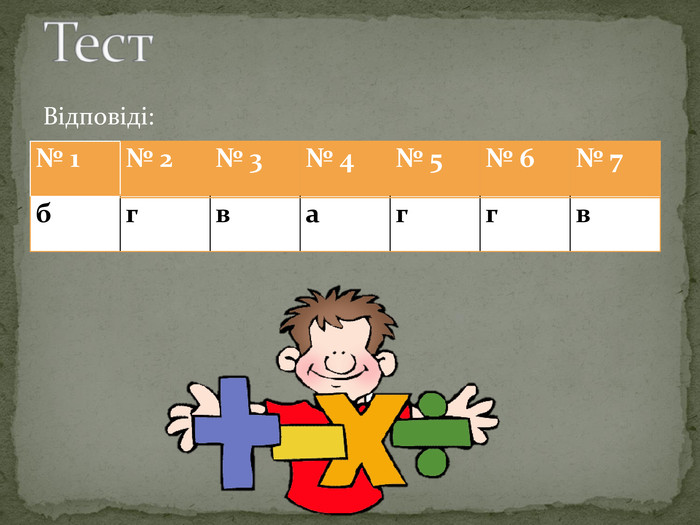
![1. Обчислити: а) 4; б) 2; в) 0,5; г) 8 2. Обчислити: а) -2; б) - ; в) 34; г) розв’язку немає 3. При яких значеннях х вираз має зміст: а)[0;∞) ; б) (-∞;5]; в) (-∞;∞); г) [5;∞). 4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -2 5. Розв’язати рівняння: а) 11; б) 21; в) -16; г) 121 6. Розв’язати рівняння: а) 2; б) 265; в) -265; г) коренів немає 7. Розв’язати рівняння: а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5. 1. Обчислити: а) 4; б) 2; в) 0,5; г) 8 2. Обчислити: а) -2; б) - ; в) 34; г) розв’язку немає 3. При яких значеннях х вираз має зміст: а)[0;∞) ; б) (-∞;5]; в) (-∞;∞); г) [5;∞). 4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -2 5. Розв’язати рівняння: а) 11; б) 21; в) -16; г) 121 6. Розв’язати рівняння: а) 2; б) 265; в) -265; г) коренів немає 7. Розв’язати рівняння: а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.](/uploads/files/366989/97113/103579_images/16.jpg)












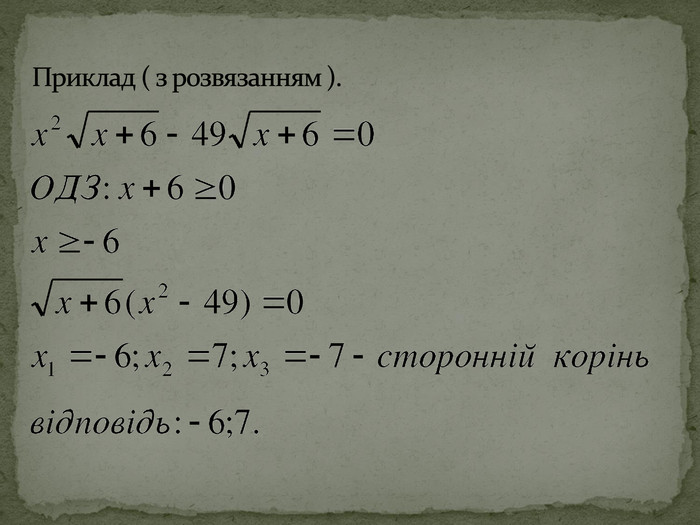








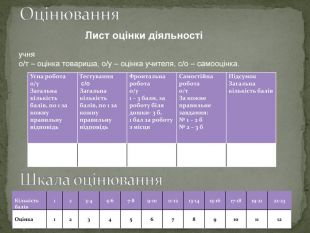
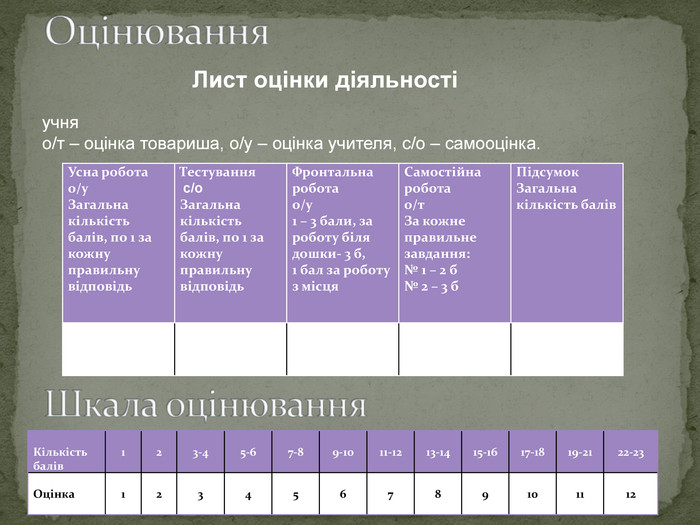
Усна робота о/у Загальна кількість балів, по 1 за кожну правильну відповідь Тестування с/о Загальна кількість балів, по 1 за кожну правильну відповідь Фронтальна робота о/у 1 – 3 бали, за роботу біля дошки- 3 б, 1 бал за роботу з місця Самостійна робота о/т За кожне правильне завдання: № 1 – 2 б № 2 – 3 б Підсумок Загальна кількість балів Кількість балів Оцінка Лист оцінки діяльності учня о/т – оцінка товариша, о/у – оцінка учителя, с/о – самооцінка.
Давньогрецький учений-дослідник, який вперше довів існування ірраціональних чисел 1.Що необхідно виконати для отриманих значень змінної при розв'язуванні ірраціональних рівнянь? 2.Спосіб, яким проводиться перевірка розв'язків ірраціональних рівнянь? 3.Як називається знак кореня? 4.Як називаються рівняння, в яких під знаком кореня міститься змінна? 5.Як називається корінь третього степеня? 6.Скільки коренів має рівняння х2=а, якщо а <0? перевірку підстановка радикал ірраціональні кубічний жодного
Евклід – великий вчений, який жив у ІІІ столітті до нашої ери в Стародавній Греції. Був запрошений в Олександрію царем Птоломеєм І для організації математичної школи. Евклід відомий усьому світові завдяки своїй праці «Начала», яка складається з 13 книг, до яких пізніше додали 14 та 15 книги. За «Началами» Евкліда протягом багатьох століть вивчали геометрію в усіх школах. Евклід – початок ІІІ ст. до н.е.
1.Скільки розв'язків має рівняння х2=0? 2.Корінь якого степеня існує з будь-якого числа? 3.Як називається корінь другого степеня? 4.Скільки коренів має рівняння х2=а, якщо а >0? 5.Корінь якого степеня існує лише з невід'ємного числа? 6.Як називається корінь рівняння, який утворюється в результаті нерівносильних перетворень? один непарного квадратний два парного сторонній
рівняння корінь комп'ютер Вієта рівносильні спряжені 1.Як називається рівність в якій міститься змінна? 2.Як називається значення змінної, при якому рівняння перетворюється на вірну числову рівність? 3.”Мовчазний” вчитель сучасного учня? 4.Яку теорему використовують при розв'язуванні квадратних рівнянь? 5.Як називаються рівняння, якщо вони мають одні й ті самі корені або не мають корені взагалі? 6.Як називаються ірраціональні вирази, що містять протилежні арифметичні дії “-” та “+”?
1. Обчислити: а) 4; б) 2; в) 0,5; г) 8 2. Обчислити: а) -2; б) - ; в) 34; г) розв’язку немає 3. При яких значеннях х вираз має зміст: а)[0;∞) ; б) (-∞;5]; в) (-∞;∞); г) [5;∞). 4. Розв’язати рівняння: а) 4; б) 2; в) 16; г) -2 5. Розв’язати рівняння: а) 11; б) 21; в) -16; г) 121 6. Розв’язати рівняння: а) 2; б) 265; в) -265; г) коренів немає 7. Розв’язати рівняння: а) 1; -3,5; б) 1; 3,5; в) -1; г) -1; -3,5.
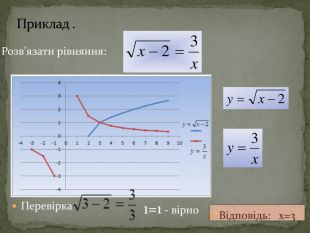
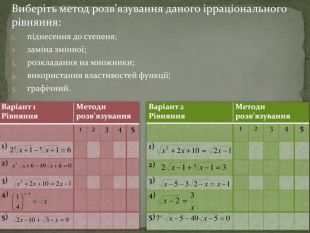
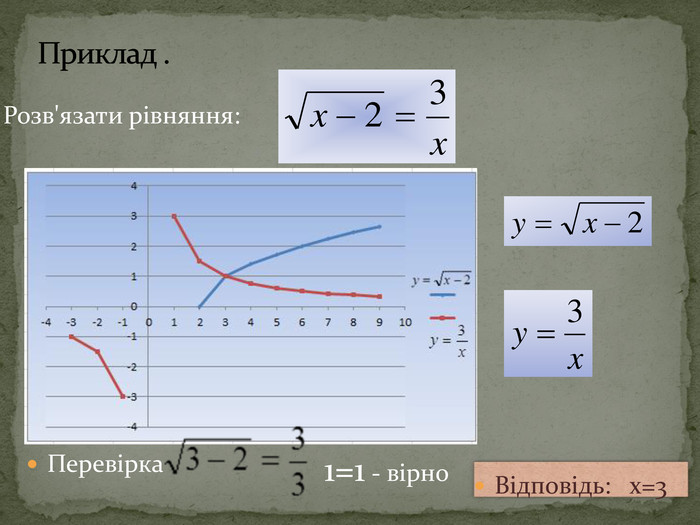
Основні ідеї: Графічний метод базується на побудові графіків відповідних функцій, які стоять в обох частинах рівняння, та знаходженні їхніх точок перетину, що є відповідно розв’язками даного рівняння. Недоліком даного методу, є те, що для більшості функцій ми не зможемо знайти точного розв’язку.
-
 Мельник Сергій Олексійович 16.05.2021 в 10:46Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Мельник Сергій Олексійович 16.05.2021 в 10:46Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0


про публікацію авторської розробки
Додати розробку