Творчий проект на тему "Цікаві числа в математиці"

Київське вище професійне училище будівництва і дизайну

Творчий проект на тему:

«Цікаві числа

в математиці»

Підготувала:

Викладач математики

   Р.І. Кулацька

Київ ­­– 2018

Зміст

1.               Історія виникнення чисел………………………………….……3
2.               Комплексні числа……………………………………….……….5
3.               Досконалі числа…………………………………………………7
4.               Дружні числа………………………………………………..… 8
5.               Числа-велетні та числа-карлики……………….…………….. 9
6.               Фігурні числа………………………………………………..… 11
7.               Число π……………………………………………………….... 13
8.               Число е……………………………………………………….... 14
9.               Числа Фібоначчі……………………………………………...…15
10.          Цікаві факти про числа……………………………………..… 18

1.               Історія виникнення чисел

Поняття натурального числа, викликане потребою лічби предметів, виникло ще в доісторичні часи. Процес формування поняття натурального числа тривав протягом усієї історії людства. На найнижчому етапі первісного суспільства поняття абстрактного числа не існувало. Аналіз мов первісних народностей показує, що для лічби предметів різного типу використовувалися різні словесні обороти. Такі іменовані числові ряди були дуже короткими і завершувалися поняттям «багато» або різними словами для різних типів об'єктів, такими, як «натовп», «стадо», «купа» тощо.

Спочатку числові терміни мали якісніший характер — відрізняли один, два та більшу кількість. Більші числа одержували додаванням. Але навіть такі здібності людство здобуло після великого проміжку часу, в який користувалися лише з понять «один», «два» та «багато» (ще й досі збереглося плем'я, яке зупинилося на цьому етапові розвитку вмінь числового абстрагування).

Джерелом виникнення поняття абстрактного числа була лічба предметів. У більшості народів першим таким еталоном були пальці («лічба на пальцях»). На цьому етапі число стає абстрактним, незалежним від якості об'єктів лічби. Розширення потреб лічби спонукало людей інші елементи лічби, наприклад, зарубок на паличці. Для фіксації порівняно великих чисел стала використовуватися нова ідея: позначення деякого певного числа (у більшості народів — десяти) новим знаком, наприклад, зарубкою на іншій паличці.

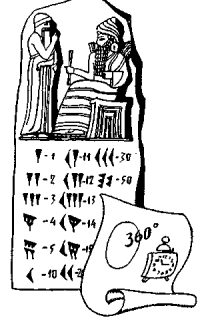З розвитком писемності можливості відтворення чисел значно розширились. Спочатку числа стали позначати рисками на матеріалі, що слугував для запису (папірус, глиняні таблички тощо). Потім були введені інші знаки для великих чисел. Вавилонські клинописні позначення чисел, а також «римські цифри», що збереглися до наших днів, ясно свідчать саме про цей шлях формування позначень для чисел.

Великим прогресом було винайдення «цифр». Тепер стало можливим записати будь-яке число обмеженим набором символів. Наприклад, вавилоняни розвинули потужну позиційну систему, що базувалася на цифрах 1 та 10, але фактично її основою було число 60. Зручнішою була індійська позиційна система числення, що дозволяла записати будь-яке натуральне число за допомогою десяти знаків — цифр; вона згодом стала всесвітньо визнаною і досі залишається такою (хоча форма цифр дещо змінювалася; цифри цієї системи ми називаємо арабськими, оскільки система прийшла в Європу через арабів). Таким чином, паралельно з розвитком писемності, поняття натурального числа приймає все більш абстрактну форму, відокремлену від будь-якої конкретності поняття числа, відтворюваного як у формі слів в усній мові, так і в формі позначення спеціальними знаками в письмовій.

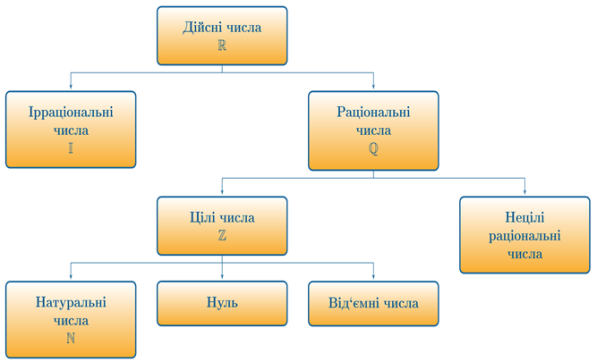
Множина натуральних чисел включає в себе цілі додатні числа. Позначається ця множина N. Множина цілих чисел позначається Z і включає в себе натуральні числа та протилежні їм числа (від’ємні) і число 0. Об’єднавши цілі числа із дробовими, отримаємо раціональні числа. Множина раціональних чисел позначається Q. Раціональні числа можна подати у вигляді нескоротного дробу , де  — ціле число,  — натуральне число (записується у вигляді нескінченного періодичного десяткового дробу).

Множина раціональних чисел включає в себе числа, які можна записати у вигляді нескінченного неперіодичного десяткового дробу.  Раціональні та ірраціональні числа утворюють множину дійсних чисел. Це числа, які можна подати у вигляді нескінченного десяткового дробу. Позначається множина дійсних чисел R.

2.               Комплексні числа

У багатьох розділах математики та її застосуваннях неможливо обмежитися розглядом лише дійсних чисел. Вже досить давно під час розв’язування різних задач виникла потреба добувати квадратний корінь з від’ємних чисел. Але чисел, які при піднесенні до квадрата дають від’ємні числа, тоді не знали і тому вважали, що квадратні корені в від’ємних чисел не існують, тобто задачі, які до них приводять, не мають розв’язків.

Тому природно постало питання про розширення множини дійсних чисел, приєднанням до неї нових так, щоб у розширеній множині, крім чотирьох арифметичних дій – додавання, віднімання, множення і ділення (за винятком ділення на нуль), можна було виконувати дію добування кореня. Це питання було успішно розв’язане лише у ХІХ ст.

Оскільки існує вимога, щоб у новій числовій множині рівняння мало розв’язок, необхідно ввести деяке нове число, вважаючи його розв’язком цього рівняння. Число, квадрат якого дорівнює –1, позначають буквою і і називають уявною одиницею (і – перша буква латинського слова imaginarius – уявний).

Числа виду , де aі b- довільні дійсні числа, а i- уявна одиниця називають комплексними . Слово “комплексний” означає складений. Число aназивають дійсною частиною комплексного числа , а вираз bi- уявною.

Два комплексних числа a+bi і c+di рівні між собою тоді і тільки тоді, коли a=c і b=d, тобто, коли рівні їх дійсні частини і коефіцієнти при уявних частинах.

Поняття “більше” і “менше” для комплексних чисел не має смислу. Ці числа за величиною не порівнюють.

Геометрична інтерпретація комплексних чисел

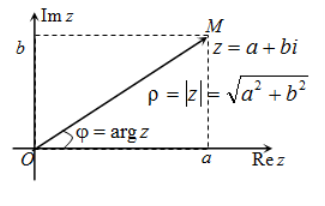Вивчаючи комплексні числа, можна використовувати геометричну термінологію і геометричні міркування, якщо встановити взаємно однозначну відповідність між множиною комплексних чисел і множиною точок координатної площини. Цю відповідність можна встановити так. Кожному комплексному числу поставимо у відповідність точку координатної площини, тобто точку, абсциса якої дорівнює дійсній частині комплексного числа, а ордината – коефіцієнту уявної частини.

Кожній точці координатної площини поставимо у відповідність комплексне число. Очевидно, що така відповідність є взаємно однозначною. Вона дає можливість інтерпретувати комплексні числа як точки деякої площини, на якій вибрано систему координат. Координатну площину називають при цьому комплексною , вісь абсцис – дійсною віссю, бо на ній розміщені точки, що відповідають комплексним числам , тобто відповідають дійсним числам. Вісь ординат називається уявною віссю – на ній лежать точки, які відповідають уявним комплексним числам .

Зручною є також інтерпретація комплексного числа як вектором (див. рис. 1). Поставимо у відповідність кожному комплексному числу вектор з початком у точці і кінцем у точці . Ви знаєте, що такий вектор називають радіусом-вектором, а його проекції на осі координат є координатами вектора. Отже, можна сказати, що геометричним зображенням комплексного числа є радіус-вектор з координатами і . Відповідність між множиною комплексних чисел, з одного боку, і множиною точок або векторів площини, з іншого, дає змогу комплексні числа називати точками або векторами і говорити, наприклад, про вектор або про точку .

3.               Досконалі числа

Досконале число — натуральне число, яке дорівнює сумі всіх своїх дільників крім самого числа. Всього їх знайдено 24.

Найменшим досконалим числом є число 6{\displaystyle 6=3+2+1\,}, наступне досконале число — число 28.

Перші два досконалі числа були відомі ще в глибоку давнину. Наступні два — 496 і 8 128 знайшов в IV столітті до н. е. Евклід і тільки через півтори тисячі років було знайдене ще одне досконале число — 33 550 336. До середини XX століття було знайдено ще 7 таких чисел. Починаючи з 1952 року для пошуку досконалих чисел почали застосовувати ЕОМ і якщо перше досконале число (6) однозначне, то 24-те має понад 12 000 знаків.

Евклід не тільки відшукав два досконалих числа, а і дав ключ до пошуку парних досконалих чисел. Він довів досконалість чисел які можна представити у вигляді {\displaystyle 2^{p}-1}{\displaystyle 2^{p-1}(2^{p}-1)}, де {\displaystyle 2^{p}-1} — просте число. Усі відомі досі досконалі числа парні, проте не існує доказу того, що непарних досконалих чисел немає.

В XVII столітті досконалі числа шукав французький  математик  Мерсенн. Він припустив, що при р=17, 19, 31, 67, 127 і 257 формула Евкліда дає досконале число. Проте перевірити своє припущення не зумів через складність обчислень. Правоту Мерсенна для р=17, 19 і 31 довів в XVIII столітті Леонард Ейлер. Пізніше виявилась помилковість передбачень для р=67 і 257.

Свою назву числа отримали тому що в давнину їм приписувалося особливе містичне значення. Через складність їх знаходження і таємничу непосяжність в давнину вони вважались божественними. Так, середньовічна церква вважала, що вивчення досконалих чисел веде до спасіння душі і тому хто знайде наступне досконале число гарантоване вічне блаженство. Існувало також переконання, що світ саме тому прекрасний, що створений за 6 днів, а людство не досконале, тому що походить від недосконалого числа 8, оскільки 8 людей врятувалося на Ноєвому ковчезі від всесвітнього потопу. Проте на тому ж ковчезі врятувалося ще 7 пар нечистих і 7 пар чистих тварин, що в сумі становить 28 — досконале число. Існує чимало подібних збігів. Наприклад руки людини можна назвати досконалим знаряддям, оскільки в 10 пальцях знаходиться 28 фаланг.

4.               Дружні числа

Дружніми числами називають два натуральні числа такі, що сума всіх дільників першого (за винятком самого числа) рівна другому числу, а сума всіх дільників другого числа (за винятком самого числа) рівна першому числу. Наприклад для 220 такими дільниками є числа 1, 2, 4, 5, 10, 11, 20, 22, 44, 55 і 110 сума яких рівна 284, а для 284 дільниками є 1, 2, 4, 71, і 142 сума яких рівна 220. Отже (220,284) є парою дружніх чисел. Найменшими парами дружніх чисел є (220, 284), (1184, 1210), (2620, 2924) (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084).

В історії математики вони були обчислені в різних країнах і в різний час:

1.               220 і 284 ( Піфагор, близько 500 до н. е..)
2.               1184 і 1210 (Ніколо Паганіні (тезка великого скрипаля), 1860)
3.               2620 і 2924 ( Л.Ейлер, 1747)
4.               5020 і 5564 ( Л.Ейлер, 1747)
5.               6232 і 6368 ( Л. Ейлер, 1750)
6.               10744 і 10856 ( Л.Ейлер, 1747)
7.               12285 і 14595 (Браун, 1939)
8.               17296 і 18416 ( Ібн ал-Банна, близько 1300, П'єр Ферма, 1636)
9.               63020 і 76084 ( Л.Ейлер, 1747)
10.          66928 і 66992 ( Л. Ейлер, 1750)
11.          67095 і 71145 ( Л.Ейлер, 1747)
12.          69615 і 87633 ( Л.Ейлер, 1747)
13.          79750 і 88730 (Рольф (Rolf), 1964).

Ейлер дав список 64 пар таких чисел, хоча деякі потрапили в список дружніх чисел помилково. У 1867р. 16-літній Ніколо Паганіні (тезка геніального скрипаля) встановив, що 1184 і 1210 дружні числа, їх прогледіли всі відомі математики. Зараз відкрито понад 600 пар дружніх чисел.  Усі знайдені пари таких чисел однакової парності. Коли обидва числа пари непарні, число 3 є їх спільним дільником. Невідомо, яка потужність множини пар дружніх чисел і чи поширюються відомі властивості цих пар на всі пари.
Дружні числа продовжують приховувати безліч таємниць. Чи є змішані пари, у яких одне число парне, а інше не парне? Існує загальна формула, що описує всі дружні пари? На ці та інші питання відповіді поки не знайдені.

5.               Числа-велетні та числа-карлики

У повсякденному житті нам здебільшого доводиться зустрічатися з порівняно невеликими числами, так що люди часто не мають правильного уявлення про спів­відношення між великими числами і малими.

Щоб наша думка була зрозумілою, наведемо кілька прикладів, де ми маємо справу з надзвичайно великими числами, тобто числами-велетнями, і надзвичайно малими, тобто числами-карликами.

Відстань від Землі до Сонця в сантиметрах приблизно дорівнює 1,5 · 10¹³, а відстань до  Плутона — найбільш віддаленої від Сонця планети — дорівнює 6 · 10¹⁴ см.Об'єм кулі, що вміщає в собі всю сонячну систему, не перевищує 10⁴⁵ куб. см.Маса Сонця дорівнює приблизно 2 · 10³⁶ г.Світло від Сонця до найближчої до нього зірки α Центавра проходить за 10⁸ сек.Відстань від Землі до найвіддаленіших спіральних ту­манностей, які вже вдалося спостерігати, становить близько 10²⁸ см.Число молекул в одному кіломолі речовини дорівнює 6,02 · 10²⁶.За хвилину серце робить у середньому 70 ударів, за добу — понад 100 000, за рік — 36,5 млн., а за 60 років (се­редня тривалість життя людини) — близько 2 млрд. 200 млн. ударів. Усе це — числа-велетні.

З надзвичайно малими числами особливо часто зу­стрічаються дослідники елементарних частинок.

Маса атома водню дорівнює 1,6733 · 10^-24 г.Маса електрона дорівнює 9,108 · 10^-28 г.Період життя елементарної частинки, що називається π°-мезоном, становить близько 1,8 · 10^-16 сек.

Великі числа цікавили ще стародавніх математиків. Архімед, наприклад, у своєму творі: «Псамміт» («Про число піщинок»), бажаючи переконати тих, хто вважає, що число піщинок на всій Землі не можна зобразити якимось числом, спочатку групує числа таким способом: число від 1 до міріади міріад (до 10⁴ · 10⁴ = 10⁸) він на­зиває «першими» числами; число 10⁸ — одиницею «других» чисел, які йдуть від цієї одиниці до міріади міріад таких одиниць (від 10⁸ до 10¹⁶). Число 10¹⁶ називається одини­цею «третіх» чисел; треті числа йдуть від 10¹⁶ до 10²⁴. Продовжуючи таку побудову, Архімед доходить до мірі­ади міріад чисел «міріадоміріадних». Потім він пояснює процес побудови ще більших чисел і доводить, що весь «всесвіт», який, на його думку, займає сферу з діаметром 10¹⁰ стадій (одна стадія дорівнює приблизно 190 м),може вмістити не більш як 10⁵¹ піщинок.

6.               Фігурні числа

Фігурні числа — загальна назва чисел, пов'язаних з тією або іншою геометричною фігурою .

Припускають, що вперше вони з'явилися в VI столітті до нашої ери - у школі Піфагора. Надалі багато математиків цікавилися цими числами.

Числа стародавніми греками, а разом з ними Піфагором і піфагорійцями, - мислилися зримо, у вигляді камінчиків, розкладених на піску або на лічильній дошці - абаці. З цієї причини греки не знали нуля, тому що його неможливо було "побачити".

 З цих міркувань арифметика піфагорійців була тісно пов'язана з геометрією: вони виділяли класи чисел, що мають одну і ту ж форму, а саме: трикутні, квадратні, п'ятикутні  і так далі.

Лінійні числа (тобто прості числа і  1) - числа, які діляться тільки на одиницю і на самих себе і, отже, можуть бути представлені у вигляді послідовності точок, вишикуваних в лінію:

1, 2, 3, 5, 7, 11, 13, 17, 19, 23, ...

Лінійне число 5

Плоскі числа - числа,  що можна представити  у вигляді добутку двох множників, відмінних  від 1  і  самого  числа:

4, 6, 8, 9, 10, 12, 14, 15, ...

Плоске число 6

Телесні числа — числа, що можна подати добутком трьох співмножників відмінних від 1:

 8, 12, 18, 20, 24, 27, 28, ...

Тілесне число 8

Трикутні числа - це такі числа, з яких (маючи стільки камінчиків) можна викласти правильні трикутники.

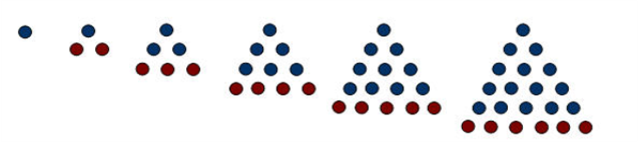
       1         3         6                10              15                   21

Квадратні числа виходять при викладанні з камінчиків квадратів:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …

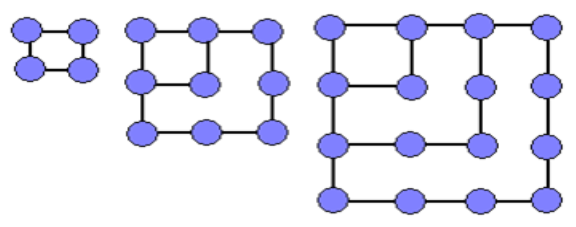
Другий - це два ряди, кожен із двух камінців: 2 ·2=4. Третій - три ряда по три камінця: 3 ·3=9.

Четвертий- 4 ряда по 4 камінця: 4·4=16.

Невипадково про такі числа говорят: «два в квадраті», «три в квадраті», «чотири в квадраті».

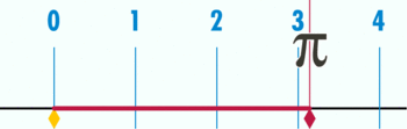
7.               Число π

Число́ пі (позначається {\displaystyle \pi }π) — математична константа, що визначається у Евклідовій геометрії як відношення довжини кола {\displaystyle l} до його діаметра {\displaystyle d}{\displaystyle \pi ={\frac {l}{d}}}або як площа круга одиничного радіуса.

Число {\displaystyle \pi } виникло в геометрії як відношення довжини кола до довжини його діаметра, проте воно з'являється і в інших областях математики. Вперше позначенням цього числа грецькою літерою π скористався британський (валлійський) математик Вільям Джонс (1706), а загальноприйнятим воно стало після робіт Леонарда Ейлера (1737). Це позначення походить від початкової букви грецьких слів περιφέρεια — оточення, периферія та περίμετρος — периметр.

Довжина кола дорівнює π, якщо його діаметр 1.

Оскільки π є ірраціональним числом, його не можна виразити дробом(або що те саме, його десяткове представлення є нескінченним та неперіодичним). Проте дроби такі як 22/7 і інші часто застосовуються для наближення числа π.

Вважається, що різні цифри у десятковому представленні числа πзустрічаються однаково часто (тобто π є нормальним числом), проте це не доведено. Також π є трансцендентним числом — тобто не є коренемжодного ненульового поліному з раціональними коефіцієнтами.

Найраніші писемні наближені значення числа {\displaystyle \pi } датуються майже 1900 роком д.н. е.; це 256/81 ≈ 3.160 (Єгипет) і 25/8 = 3.125 (Вавилон), обидва в межах 1 відсотка істинного значення.

Діаграми обчислення числа пі Архімедом

Архімед (287—212 до н.е), можливо, першим запропонував метод обчислення {\displaystyle \pi } математичним способом. Для цього він вписував у коло і описував біля нього правильні багатокутники. Приймаючи діаметр кола за одиницю, Архімед розглядав периметр вписаного багатокутника як нижню оцінку довжини кола, а периметр описаного багатокутника як верхню оцінку. Таким чином, для шестикутникавиходить {\displaystyle 3<\pi <2{\sqrt {3}}}3<π<2.

Розглядаючи правильний 96-кутник, Архімед отримав оцінку 

{\displaystyle 3+{\frac {10}{71}}<\pi <3+{\frac {1}{7}}}.

Перший значний європейський внесок з часів Архімеда зробив німецький математик Лудольф ван Цейлен (1536—1610). Він витратив десять років на обчислення числа {\displaystyle \pi }π з 20-ма десятковими цифрами.

8.               Число е

Число е зустрічається у шкільному курсі рідше, ніж число Пі, та у вищій математиці воно відіграє важливу роль і зустрічається дуже часто.

Припустимо, що хтось поклав 1$ у банк, який сплачує 4% річних. Якщо відсотки складні, то після кожного їх нарахування кількість грошей збільшуватиметься і відсотки кожного наступного разу нараховуватимуться від збільшеної загальної суми. Чим частіше робитимуть перерахунки, тим швидше збільшуватиметься вклад. Коли щороку нараховувати складні відсотки, 1$ за 25 років перетвориться у (1 + 0,04)²⁵, тобто у 2,66$. Коли нараховуватимуть складні відсотки кожні півроку, то за 25 років долар перетвориться у (1 + 0,02)⁵⁰, або 2,69$.

У рекламних проспектах банків їх автори особливо підкреслюють, скільки разів на рік нараховуються відсотки. Може скластися враження, що коли досить часто нараховувати відсотки (наприклад, мільйон разів на рік), то за 25 років долар перетвориться у досить велику суму грошей. Насправді ж цього не відбудеться. Через 25 років долар виріс би до величини

де n — кількість нарахувань прибутку. При n, що прямує до нескінченності, цей вираз прямуватиме до границі, яка дорівнює 2,718..., що лише на 3 центи більше за ту суму, яку б отримали, коли б прибуток нараховувався один раз кожні півроку. Ця границя і називається числом е.

Як і число Пі, число e — трансцендентне, тобто воно не може бути коренем якогось алгебраїчного рівняння з раціональними коефіцієнтами.

Перші 20 знаків числа е такі:

е ≈ 2,71828182845904523536.

Щоб запам'ятати їх, необхідно помітити, що після цифри 7 двічі записано рік народження Л. Толстого, а потім — кути рівнобедреного прямокутного трикутника.

Першим запровадив символ e Л. Ейлер. Йому належить так багато відкриттів, пов'язаних з числом e, що зрештою число e стали називати «числом Ейлера»

9.               Числа Фібоначчі

Великий математик XIII століття Леонардо Пізанський, найбільше відомий під прізвиськом Фібоначчі, першим помітив цікаву послідовність чисел, яка отримала назву числа Фібоначчі.

Суть залежності Фібоначчі – кожне наступне число дорівнює сумі двох попередніх. Починається ряд з нуля, і продовжувати його можна нескінченно: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

Кожне наступне число в цій послідовності є сумою двох попередніх. Приклад:

1 +1 = 2

2 +1 = 3

3 +2 = 5 і так далі …

Далі Фібоначчі виявив, що якщо взяти два сусідніх числа з цієї послідовності і вирахувати співвідношення меншого числа до більшого, то у результаті вийде 0.618, а відношення кожного числа ряду до попереднього числа = 1.618 (коефіцієнти Фібоначчі, або “Золотий переріз”). В математиці його позначають грецькою буквою фі (Ф = 1,618). Золотий переріз спостерігається в структурі багатьох природних об’єктів і явищ – від будови раковин молюсків до форми вихорів ураганів і галактики.

Можемо перевірити:

34/55 = 0.618

55/89 = 0.618

89/144 = 0.618.

Є ще одна закономірність – якщо будь-який член ряду послідовності Фібоначчі розділити не на наступне число, а на число через один, то вийде співвідношення, наближене до 0.382.

У разі якщо взяти третій член ряду після вихідного, то співвідношення між ними буде приблизно дорівнює 0.236.
У послідовності Фібоначчі, кожен елемент, починаючи з третього, є сумою двох попередніх елементів, при тому, що ряд починається з чисел 0 s 1. Отож, виходить: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025 …

Відношення двох сусідніх елементів рядунаближається до Золотого Перетину, тобто до 1,618… 

Конструкція піраміди заснована на пропорції Ф = 1,618. Це відкриття було зроблено після численних спроб розгадати секрети цієї піраміди. Сама піраміда в Гізі представляється якимсь посланням нащадкам, з тим, щоб передати певні знання законів математичної послідовності. За часів зведення піраміди її будівельники не мали достатніми можливостями для вираження відомих їм закономірностей. У ту пору не існувала писемність, не використовувалися ще й ієрогліфи. Однак творцям піраміди вдалося за допомогою геометричної пропорції свого творіння передати свої знання математичної закономірності майбутнім поколінням.

Вражає уяву той факт, що піраміди в Мексиці побудовані за таким же принципом. Мимоволі виникає припущення про будівництво мексиканських пірамід в один час з єгипетськими, до того ж будівельники володіли знаннями про закон Золотого перетину.

Не менш чудовим є прояв послідовності Фібоначчі в будові рослин.
Такий висновок можна зробити, спостерігаючи за ростом і розвитком стебел і квітів. Кожна його нова гілка, проростаючи, дає початок іншим гілкам. Розглядаючи старі і нові гілки спільно, ми виявимо число Фібоначчі в кожній з горизонтальних площин.

У будові суцвіть складноцвітих рослин знов проявляється закономірність Золотого перетину:

Іpис: 3 пелюстки

Пpімула: 5 пелюсток

Амбpозія полінолиста:13 пелюсток

Hівянік звичайний: 34 пелюстка

Айстpа: 55 і 89 пелюсток

Таким чином, сумарною послідовністю Фібоначчі легко можна трактувати закономірність проявів Золотих чисел, що зустрічаються в природі. Ці закони діють в незалежності від нашого знання, від чийогось бажання приймати або не приймати їх.

10.          Цікаві факти про числа

1. У таких країнах, як Китай, Японія і Корея число «4» вважається нещасливим. Тому поверхи з номерами, які закінчуються на «4» відсутні.

2. Центільон — це найбільше число, яке виглядає як 1 з 600 нулями. Це число було записано ще в 1852 році.

3. Число «13» — у багатьох державах також вважається невдалим. Тому поверх після «12» має позначення «14», «12А» або «М» (тринадцята літера в алфавіті).

4. Араби записують цифри справа наліво, починаючи з молодших розрядів. Тому побачивши знайомі нам арабські цифри в тексті арабських народів, ми прочитаємо їх зліва направо неправильно.

5. Цікаві факти про числа стосуються і сучасних технологій. Так, Google — одна з найпопулярніших пошукових систем. Її придумав Сергій Брін і ЛарріПейдж. Назва пошукової системи було вибрано неспроста. Так, її творці захотіли показати ту кількість інформації, яку система може обробити. У математиці число, яке складається з одиниці і ста нулів називається «гугол». Цікаво й те, що назва «Google» записано неправильно (не «googol»). Але така ідея назви засновникам сподобалася ще більше.

6. 666 — це сума всіх чисел на рулетці казино.

7. Число «13» в Греції вважається нещасливим днем тільки тоді, коли випадає у вівторок. В Італії побоюються п’ятниці 17-го. А ось статисти Нідерландів підрахували, що саме 13-го числа трапляється менше аварій і нещасних випадків, оскільки люди більш обережні і зібрані.

8. Термін «цифра» в перекладі з арабської означає «нуль». Тільки з часом дане слово почали використовувати для позначення будь-якого чисельного символу.

9. Число «7» вважається самим щасливим числом.

10. 14 березня світ відзначає Міжнародний день числа “пі” — загадкового числа 3,1415926… У 1987 році американський фізик Ларі Шоу звернув увагу на те, що 14 березня (03.14) рівно о 1:59:26 дата і час збігаються з першими розрядами числа “пі”. У Європі “День пі” відзначають також 22 липня (22.07). Значення цього дробу (22/7) є максимально наближеним до числа “пі”…