Презентація "Розв’язування квадратичних нерівностей" ( 9 клас)
Про матеріал
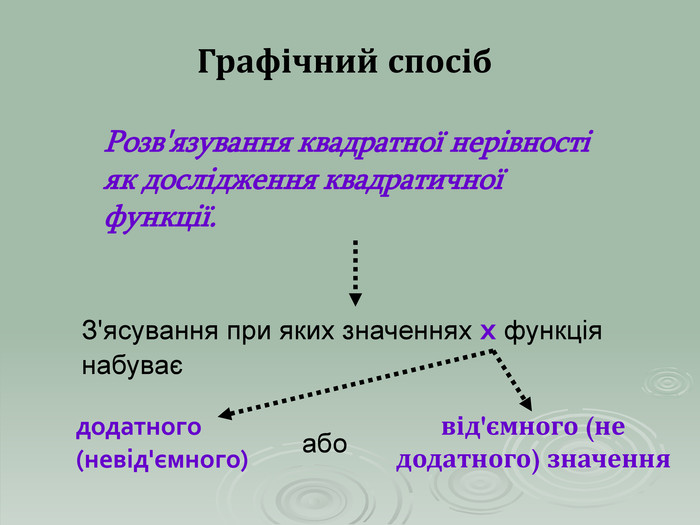
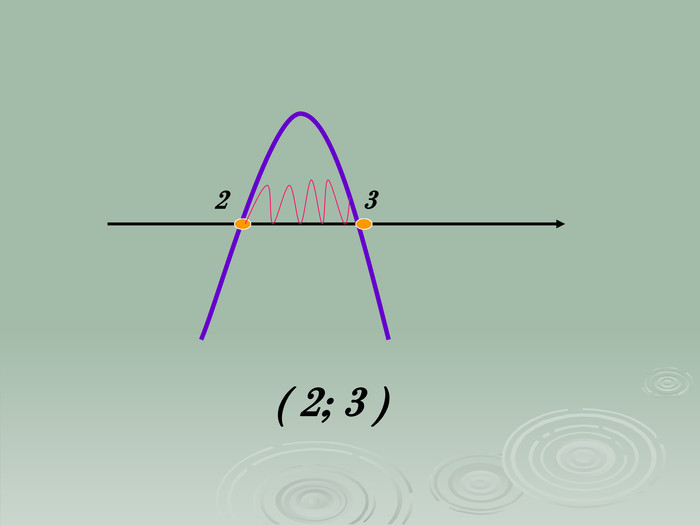
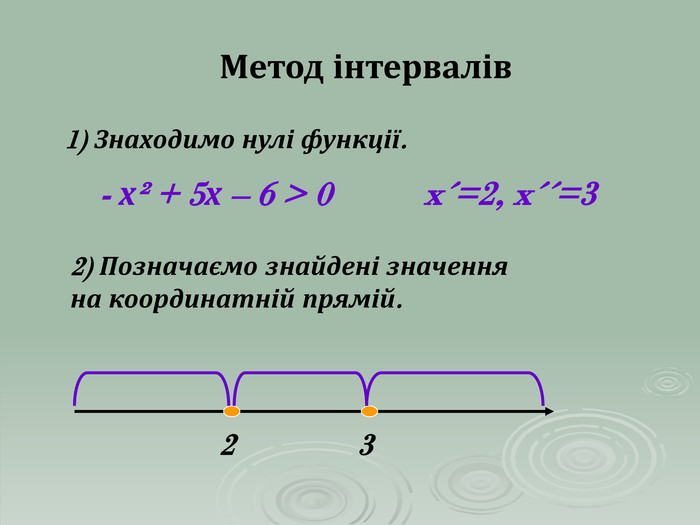
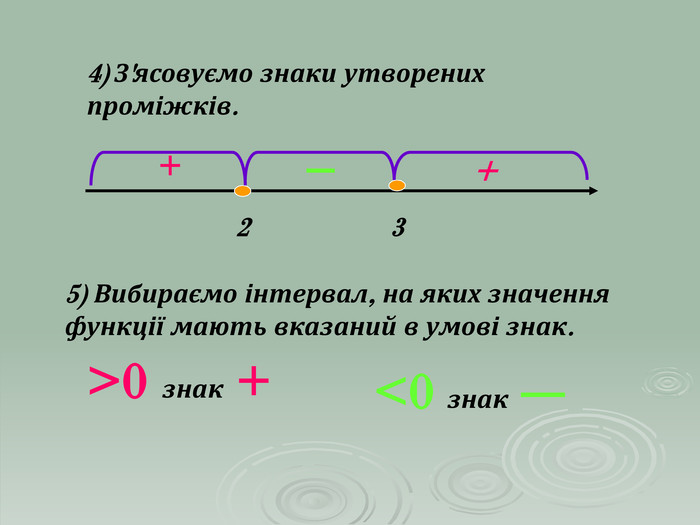
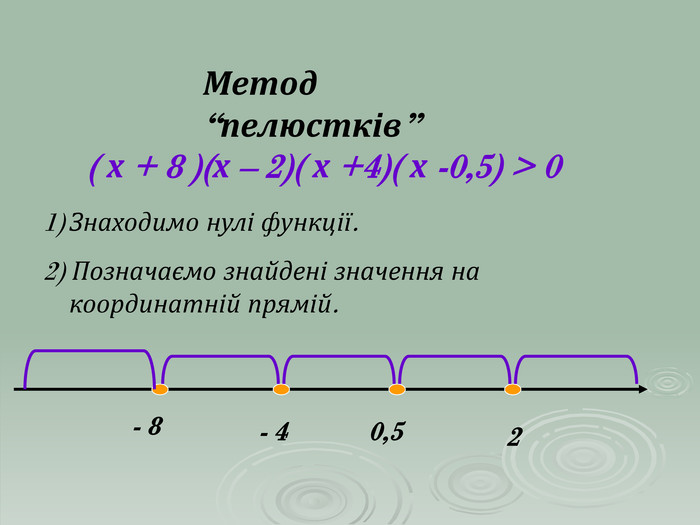
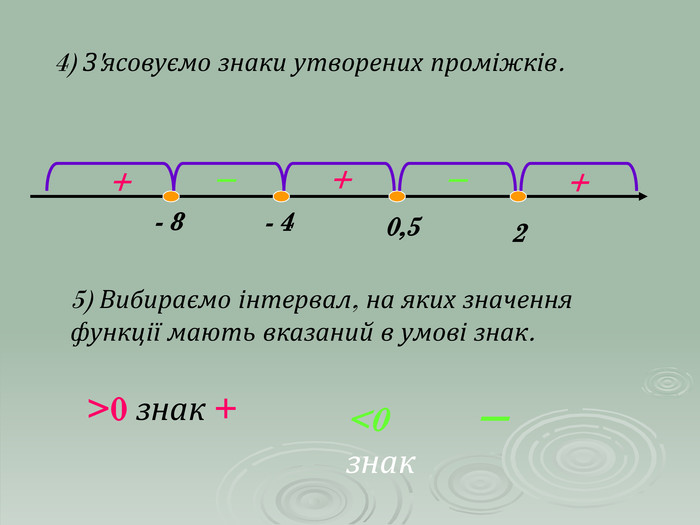
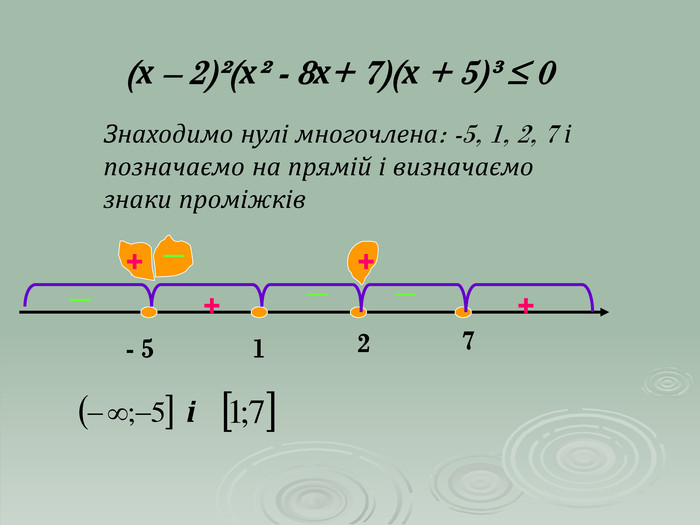
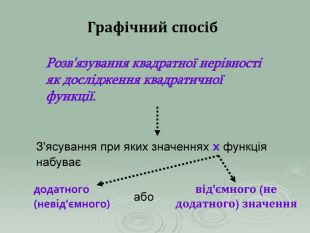
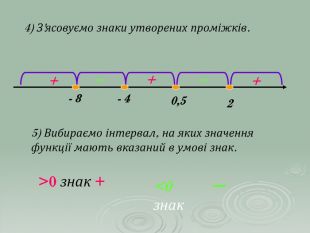
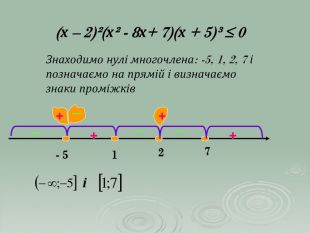
В презентації "Розв'язування квадратичних нерівностей" наведені приклади та методи розв'язування квадратичних нерівностей. Матеріали можна використовувати при проведенні самостійних робіт в 9 класі та при повторенні даного матеріалу в 11 класі.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
12. Розв’язування квадратних нерівностей Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






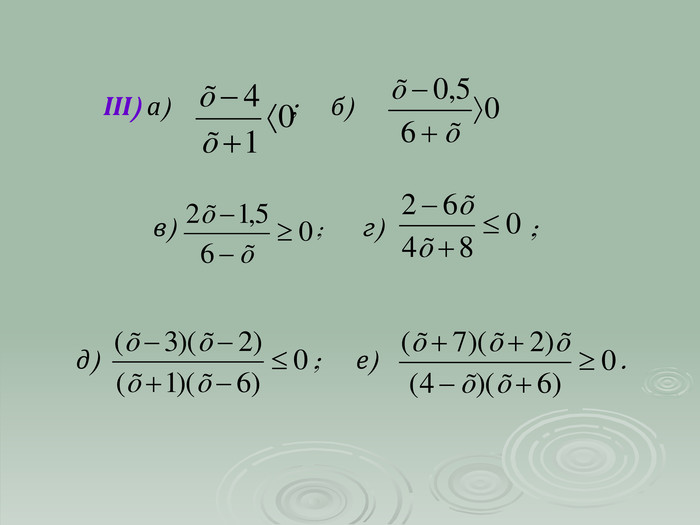











-

Крижанівська Олена
15.01.2024 в 13:21
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Кушина Антоніна Василівна
10.12.2023 в 12:15
Наталія Іванівна, дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Данилець Вікторія
15.05.2023 в 09:26
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Ирина Ирина
09.01.2021 в 13:08
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук