Урок "Статистичні дані. Способи подання даних. Частота. Середнє значення"

Тема. Статистичні дані. Способи подання даних. Частота. Середнє значення

Мета:

навчальна: сформувати в учнів уявлення про предмет вивчення математичної статистики. Працювати  над усвідомленим розумінням змісту понять: вибіркова сукупність або вибірка; статистичний ряд; частота вибірки, відносна частота вибірки; центральні тенденції вибірки (мода, медіана, середнє значення),  полігон частот та гістограма. Працювати над формуванням умінь: наводити приклади подання статистичних даних у вигляді таблиць та графіків  (гістограм); розв'язувати задачі, що передбачають подання статистичних даних у вигляді таблиць та графіків та знаходити центральні тенденції вибірки;

виховна: виховувати працьовитість, акуратність та уважність  при оформленні письмових завдань, активність, інтерес до математики;

розвиваюча: розвивати пам'ять, увагу, логічне мислення, розумову діяльність, уміння учнів робити порівняльний аналіз та систематизувати матеріал, спонукати до пізнавальної діяльності;

Обладнання: картки із завданнями, опорний конспект, презентація

Хід уроку

І. Організаційний момент

Відмітити відсутніх, перевірити готовність учнів до уроку

ІІ. Перевірка домашнього завдання

ІІІ. Повідомлення теми і мети урок

1. Яким тиражем слід випускати підручник з алгебри для 9 класу?
2. Скільки кілограмів риби і морепродуктів вживає в середньому за рік один житель України?
3. Чи вигідно для концерту певного артиста орендувати стадіон?

На ці та багато інших запитань допомагає відповісти статистика.

Термін " статистика" пішов від латинського слова " статус" (status), що означає "стан речей".

Статистика – це наука про отримання, оброблення й аналіз кількох даних, які характеризують масові явища

4.           Вивчення нового матеріалу

Статистичне дослідження складається з кількох етапів:

Давайте розглянемо подальший матеріал на прикладі:

За перший семестр ви  отримали такі оцінки з алгебри. Давайте дослідемо рівень ващої успішності.

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
БАЛИ	6	8	7	7	6	8	11	10	6	7	7	7	6	8	11	10	9	10	9	5

 

1. Згрупуємо дані за досліджуваною ознакою – рівнем успішності, і занесемо їх у таблицю таким чином

Ознака К-сть балів	1	2	3	4	5	6	7	8	9	10	11	12
Частота К-сть учнів	0	0	0	0	1	4	5	3	2	3	2	0

Таблиця такого виду називається частотною. Наприклад, частота, з якою зустрічається 7 балів, дорівнює п’яти , оскільки п’ять  учнів отримали цю оцінку.

2. Відносна частота – це відношення частоти до числа всіх усіх значень вибірки

= 20 %

3. За даними таблиці будуємо гістограму

 

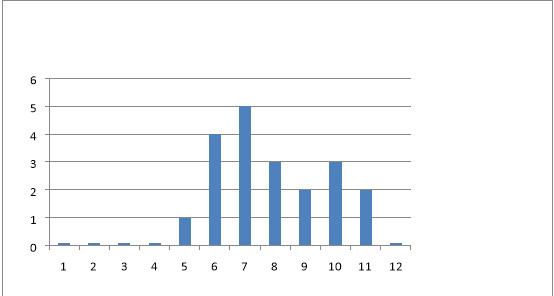
Або полігон частот

 

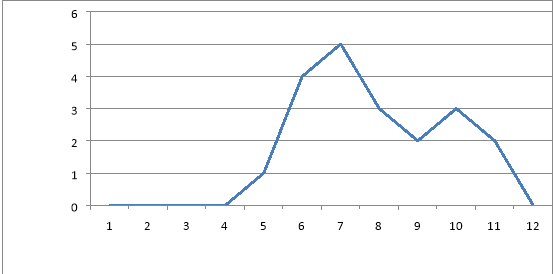
4. Знайдемо центральні тенденції:

 

• Середнє значення = =

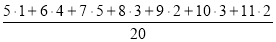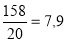
Отже, середній бал учнів нашого класу з алгебри дорівнює 7,9 бали.

• Мода вибірки – це те значення ознаки, яке трапляється найбільше, тобто має найбільшу частоту

У нашій задачі найбільша частота дорівнює 7

• Медіана вибірки – це число, яке поділяє навпіл упорядковану сукупність

Медіаною ряду, що складається з непарної кількості чисел, називається число цього ряду, яке виявиться посередині, якщо цей ряд упорядкувати.

Медіаною ряду, що складається з парної кількості чисел, називається середнє арифметичне двох чисел цього ряду, що стоять посередині

m =8.

Отже, половина учнів ( оскільки медіана «ділить» навпіл) засвоїли алгебру на рівні до семи балів.

5. Засвоєння нових знань.

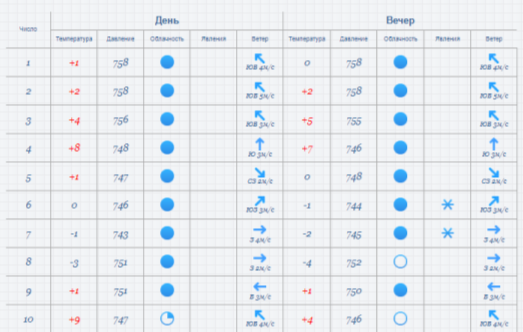
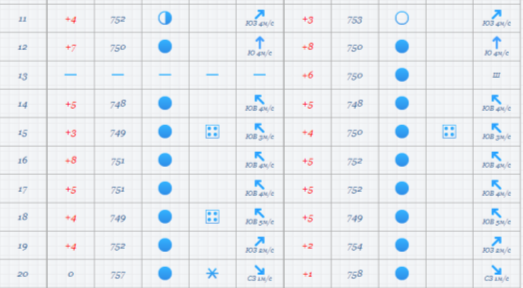
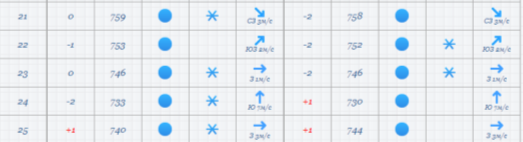
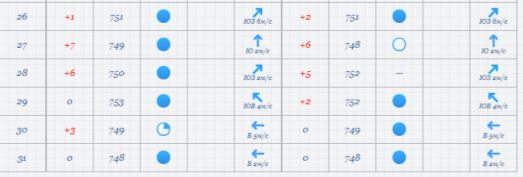
За погодними даними зібраними вами за останній місяць минулого семестру дослідити температурний режим

І варіант погоду вранці, ІІ варіант ввечері, побудувати гістограму(І вар) та полігон частот(ІІ вар) відповідно.

(Зверніть увагу приклад який ми розібрали надрукований на зворотній стороні картки з завданням)

6. Рефлексіяи

Сьогодні ми з вами розглянули математичну статистику та її основні поняття. Давайте поставимо один одному запитання про матеріал уроку. Я почну Хто відповість задає наступне запитання

• Кому належить фраза «Статистика знає все»(Остап Бендер роман 12 стільців)

7. Домашнє завдання.

Провести шкільне статистичне дослідження :

• І варіант «кількість часу проведеного за комп’ютером.»
• ІІ варіант «кількість часу витраченого на виконання домашніх завдань»

Для отриманих даних треба створити частотну таблицю, знайти центральні тенденції вибірки та побудувати гістограму або полігон частот.

ПРИКЛАД

За перший семестр ви  отримали такі оцінки з алгебри. Давайте дослідомо рівень ващої успішності.

№	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
БАЛИ	6	8	7	7	6	8	11	10	6	7	7	7	6	8	11	10	9	10	9	5

1. Згрупуємо дані за досліджуваною ознакою – рівнем успішності, і занесемо їх у таблицю таким чином

Ознака К-сть балів	1	2	3	4	5	6	7	8	9	10	11	12
Частота К-сть учнів	0	0	0	0	1	4	5	3	2	3	2	0

Таблиця такого виду називається частотною. Наприклад, частота, з якою зустрічається 7 балів, дорівнює п’яти , оскільки п’ять  учнів отримали цю оцінку.

2. Відносна частота – це відношення частоти до числа всіх усіх значень вибірки

= 20 %

За даними таблиці будуємо гістограму   Або полігон частот

3.  

 

 

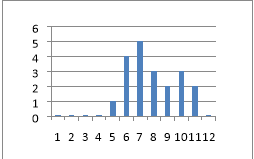
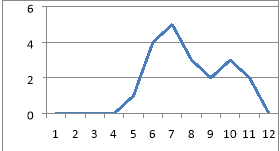
4. Знайдемо центральні тенденції:

• Середнє значення = =

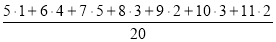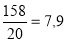
Отже, середній бал учнів нашого класу з алгебри дорівнює 7,9 бали.

• Мода вибірки – це те значення ознаки, яке трапляється найбільше, тобто має найбільшу частоту

У нашій задачі найбільша частота дорівнює 7

• Медіана вибірки – це число, яке поділяє навпіл упорядковану сукупність

Медіаною ряду, що складається з непарної кількості чисел, називається число цього ряду, яке виявиться посередині, якщо цей ряд упорядкувати.

Медіаною ряду, що складається з парної кількості чисел, називається середнє арифметичне двох чисел цього ряду, що стоять посередині

 

m =8.

Отже, половина учнів ( оскільки медіана «ділить» навпіл) засвоїли алгебру на рівні до восьми балів.

.За погодними даними зібраними вами за останній місяць минулого семестру дослідити температурний режим І варіант погоду вранці, ІІ варіант ввечері, побудувати гістограму(І вар) та полігон частот(ІІ вар) відповідно.

(Зверніть увагу приклад який ми розібрали надрукований на зворотній стороні картки)