Презентація "Розв'язування лінійних рівнянь з параметром у знаменнику"

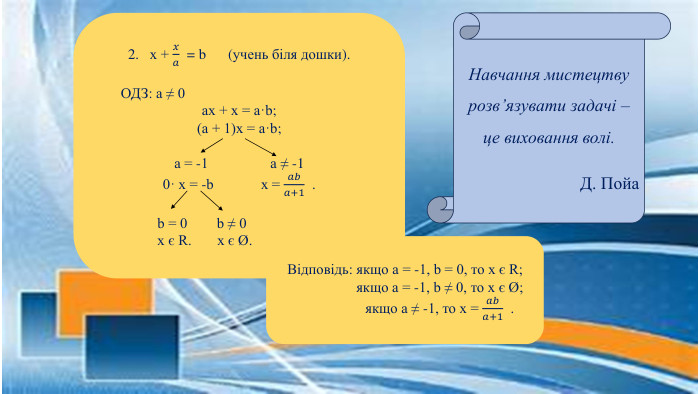
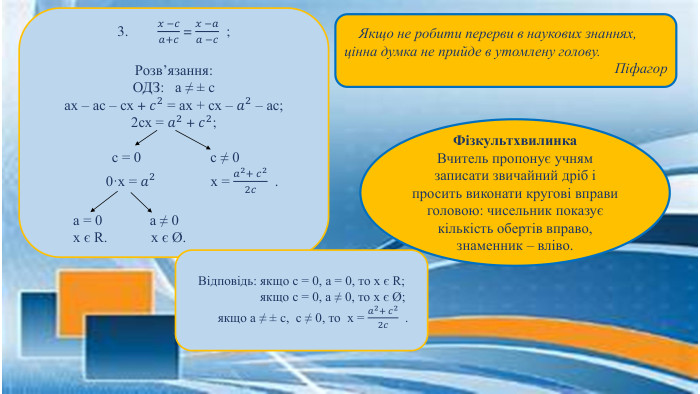
Даний матеріал можна використовувати на уроках алгебри у 7 класі при вивченні теми "Лінійні рівняння з однією змінною". Метою заняття є вдосконалення навичок розв'язування рівнянь з параметром у знаменнику за аналогією, дослідження кількості їх коренів в залежності від значень параметрів.