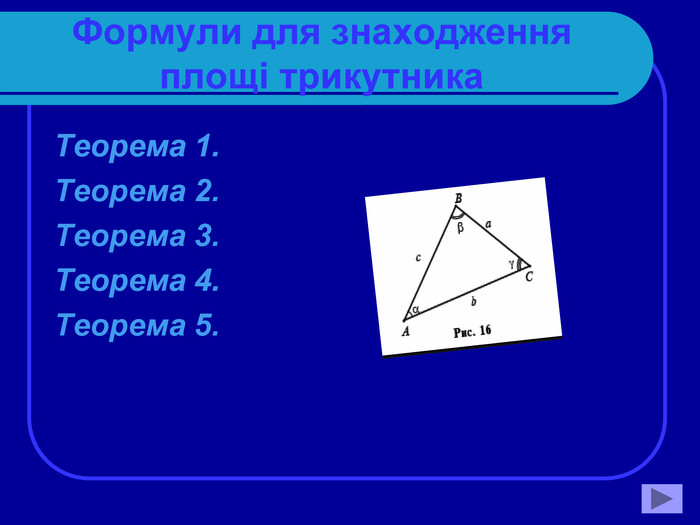
Презентація" Розв'язування трикутників.Формули для знаходження площі трикутника."
Про матеріал
Презентація "Розв'язування трикутників. Формули для знаходження площі трикутника" створена до уроку Геометрія в 9 класі.Дану презентацію можна застосовувати при вивченні теми "Застосування тригонометричних функцій до знаходження площ."
Перегляд файлу
Зміст слайдів
ppt
До підручника
Геометрія 9 клас (Єршова А. П., Голобородько В.В., Крижановський О.Ф., Єршов С. В.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку