Презентація "Розв'язування задач прикладного характеру"

Розв’язування задач прикладного характеру (задачі з використанням похідної). Урок з алгебри та початків аналізу в 10 класі. Учитель математики Ільченко Раїса Іванівна КЗ «Дергачівський ліцей №3»

“Будь – яка наука досягає вершин тільки тоді, коли вона користується математикою.” К. Марс

ТЕМА: ЗАДАЧІ З ВИКОРИСТАННЯМ ПОХІДНОЇ. Мета : ознайомитися з різними типами прикладних задач та методами їх розв’язування за допомогою похідної;формувати вміння застосовувати знання та способи дій у змінених і нових навчальних ситуаціях; поглибити знання учнів про моделювання процесів дійсності за допомогою апарата похідної. Розвивати логічне мислення, вміння аналізувати, порівнювати, розвивати пізнавальний інтерес, навички колективної праці. Розвивати вміння досліджувати, систематизувати вивчені факти. Виховувати працьовитість, зібраність, організованість, увагу, відповідальність та вимогливість до себе, волю та наполегливість у досягненні кінцевого результату. Тип уроку: засвоєння нових знань (урок із використанням методу проектів). Обладнання : комп’ютер .

Дорогі діти ! Дуже хочу , щоб ви запам’ятали слова І.Кантора “У будь-якому вченні про природу можна знайти науки стільки , скільки в ньому математики” . Ми вивчили одне із фундаментальних понять алгебри і початків аналізу – похідну. І у вас виникло питання: “А навіщо? ” На попередніх уроках ви ознайомились із застосуванням похідної для дослідження та побудови графіків функцій, знаходження найбільшого та найменшого значень функції на відрізку. А сьогодні ви на уроці дізнаєтеся, як за допомогою похідної можна розв’язати задачі з фізики , економіки та цікаві задачі прикладного характеру.

ФРОНТАЛЬНЕ ОПИТУВАННЯ Дайте означення похідної функції в точці. У чому полягає геометричний зміст похідної? (використання таблиці Неліна Є.П. “Похідна”) У чому полягає механічний зміст похідної? Як знайти похідну суми, добутку, частки ? Назвіть схему дослідження функції для побудови її графіка. (на прикладі домашнього завдання) Як знайти найбільше та найменше значення функції на відрізку? (на прикладі домашнього завдання)

ГРУПА “ІСТОРИКІВ” Девіз: “Разом навчатися не тільки легше й цікавіше, але й значно ефективніше” Завдання : з’ясувати, хто з учених і коли ввів поняття похідної.

Працюючи над проектом «Історія виникнення похідної», ми зрозуміли що, слова Є. С. Полата «Разом навчатися не тільки легше й цікавіше, але й значно ефективніше» цілком правдиві. Переконані, що похідна — одне з фундаментальних понять математики. Відкриттю похідної та основ диференціального числення передували роботи французьких математиків П’єра Ферма (1601-1665), який 1629 року запропонував способи знаходження найбільших і найменших значень функцій, проведення дотичних до довільних кривих (ці способи фактично спиралися на застосування похідних), а також Рене Декарта (1596-1650), який розробив метод координат і основи аналітичної геометрії.

У 1670-1671рр. англійський математик і механік Ісаак Ньютон (1643-1727) і дещо пізніше у 1673-1675 pp. німецький філософ і математик Готфрід Вільгельм Лейбніц (1646-1716) незалежно один від одного побудували теорію диференціального числення. І. Ньютон дійшов поняття похідної, розв’язуючи задачі про миттєву швидкість, а Лейбніц — розглядаючи геометричну задачу про проведення дотичної до кривої. Термін «похідна» увів 1797 року французький математик Жозеф Луї Лагранж (1736-1813). Він увів і сучасні позначення для похідної — у' та f' . До Лагранжа похідну, на пропозицію Лейбніца, називали диференціальним коефіцієнтом і позначали

Велику роль у розвитку диференціального числення відіграли дослідження видатного математика, фізика, механіка й астронома Леонарда Ейлера, який написав підручник «Диференціальне числення» (1755). За допомогою диференціального числення було розв’язано низку задач теоретичної механіки, фізики, астрономії. Зокрема, використовуючи методи диференціального числення, вчені передбачили повернення комети Галлея, що стало тріумфом науки XVIII ст. За допомогою цих методів математики XVIII ст. вивчали властивості різних кривих, знайшли криву, якою найшвидше падає матеріальна точка, навчилися знаходити кривизну ліній. І тепер поняття похідної широко застосовується в різних галузях науки та техніки.

Ці задачі не прості Застосуєш їх в житті. Ну а щоб їх розв’язати — Похідну слід добре знати.

Група “Пошук” Девіз: «Математику не можна вивчати, спостерігаючи, як це робить сусід». Завдання : знайти задачі з фізики ,які розв’язуються за допомогою похідної

швидкості та прискорення прямолінійного руху тіла чи матеріальної точки; кутової швидкості тіла обертання; швидкості зростання маси кристалів; швидкості зміни температури в результаті нагрівання; визначення освітленості електричної лампочки.

Посудина з вертикальною стінкою і висотою h розміщена на горизонтальній площині. На якій глибині треба розмістити отвір, щоб дальність витікання води з отвору була найбільшою (швидкість рідини, що витікає, за законом Торрічеллі дорівнює , де х — глибина розміщення отвору, g — прискорення вільного падіння)?

Розв’язання Позначимо через H відстань від отвору в посудині до горизонтальної площини, а через L – відстань від точки A до стінки посудини. Тоді L = vt, де t – час витікання води від отвору до площини (у точку A). З курсу фізики відомо, що або Тоді Знайдемо похідну: Розв’язуючи рівняння знаходимо стаціонарну точку Оскільки це єдина стаціонарна точка, то вона й буде шуканою. Відповідь . h L A H x

Група “Знавці” Девіз : “Усе, що пізнаю, я знаю, для чого це мені потрібно, де і як застосовувати можу ці знання” (В. Кильпатрик). Завдання: ознайомитись із задачами, що зустрічаються в економіці.

визначення загальної вартості утримання різних видів транспорту; визначення продуктивності праці; визначення попиту на товари, зміни прибутку в результаті підвищення ціни; визначення витрат підприємств залежно від об’єму продукції, що випускається; знаходження оптимальних розмірів продукції з найбільшим (найменшим) об’ємом (площею).

Задача Вартість (за годину) утримання баржі складається з двох частин: вартості палива, що пропорційна кубу швидкості баржі, і вартості амортизації баржі (заробітна плата команди, обладнання та ін.). Загальна вартість утримання баржі за годину, таким чином, виражається формулою S=av3+b, де v — швидкість судна у км/год; а і b — коефіцієнти, задані для кожного судна. Визначте, за якої швидкості загальна сума утримання на 1 км шляху буде найменшою, якщо а = 0,005, b = 40.

РОЗВ’ЯЗАННЯ: За умовою а = 0,005, b=40, тоді S = 0,005v3 +40. Баржа подолає 1 км шляху за год. За цей час витрати складуть   Треба знайти найменше значення функції на проміжку (0; ∞). звідки Якщо похідна функції S(v) неперервна на проміжку (0;+ ∞) і v = — одна стаціонарна точка, то вона є точкою мінімуму, оскільки Відповідь. 16 км/год.

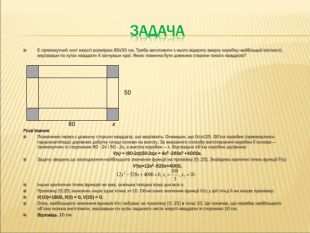
Є прямокутний лист жерсті розміром 80x50 см. Треба виготовити з нього відкриту зверху коробку найбільшої місткості, вирізавши по кутах квадрати й загнувши краї. Якою повинна бути довжина сторони такого квадрата?   Розв’язання Позначимо через x довжину сторони квадрата, що вирізають. Очевидно, що 0≤x≤25. Об’єм коробки (прямокутного паралелепіпеда) дорівнює добутку площі основи на висоту. За вказаного способу виготовлення коробки її основа — прямокутник зі сторонами 80 - 2х і 50 - 2х, а висота коробки — х. Відповідно об’єм коробки дорівнює: V(x) = (80-2x)(50-2x)x = 4x3 -260x2 +4000x. Задачу зведено до знаходження найбільшого значення функції на проміжку [0; 25]. Знайдемо критичні точки функції F(x): V'(x)=12x2 -520x+4000, Інших критичних точок функція не має, оскільки похідна існує для всіх x. Проміжку [0;25] належить лише одна точка х=10. Обчислимо значення функції V(x) у цій точці й на кінцях проміжку: V(10)=1800, V(0) = 0, V(25) = 0. Отже, найбільшого значення функція V(x) набуває на проміжку [0; 25] в точці 10. Це означає, що коробку найбільшого об’єму можна виготовити, вирізавши по кутах заданого листа жерсті квадрати зі стороною 10 см. Відповідь. 10 см. 50 x 80

ГРУПА «ЕНТУЗІАСТИ» «Недостатньо лише мати гарний розум, головне — це добре застосувати його» Найхарактерніші задачі: дослідження та побудова графіків функцій; знаходження найбільшого та найменшого значень функції на відрізку; розв’язування рівнянь; доведення нерівностей; розв’язування завдань із параметрами; наближені обчислення.

φ(х) g(x) (або φ(х)  g(x) ) за допомогою похідної, використовують таку схему: 1. Розглянути допоміжну функцію f(х)= φ(х) - g(x) на її області визначення або на заданому проміжку. 2. Дослідити за допомогою похідної поведінку функції f(х) (зростання чи спадання або її найбільше чи найменше значення ) на розглянутому проміжку. 3. Обгрунтувати ( спираючись на поведінку функції f(х) ) ,що f(х) 0 (або f(х)  0 ) на розглянутому проміжку, і зробити висновок,що φ(х) g(x) (або φ(х)  g(x) ) на цьому проміжку.

Задача. Доведіть, що sin х < х для всіх х > 0. Доведення:  Розглянемо функцію f(х) = x-sin x. f′(x)=1-cos x ≥ 0 для всіх х ϵ R. Отже, f(x) зростає на R. Якщо х > 0, то f(x) > f(0), тобто x – sin x > 0 або sin x < x.

Обчислити наближене значення функції f(x)=x7 – 2x6 + 3x2 – x + 3 у точці x = 2,02. Розв’язання: Значення f у близькій до 2,02 точці x0=2 знаходимо легко: f(2)=13. Графік f в околі точки 2 близький до прямої y=f(x0)+f ‘(x0)(x –x0) – дотичної до нього в точці з абсцисою 2. Тому f(2,02)=y(2.02) Маємо: f’(x) = 7x6 – 12x5 + 6x – 1, f’(x0) = f’(2) =75 і f(x) ≈ y(x) = 13 + 750,02 = 14,5. Обчислення на калькуляторі дають результат 14,57995.

Група “Журналістів” газети “Шкільні новини” Інтерактивна гра “Мікрофон” Над якою темою працювали на уроці? Що нового дізналися? Чого навчилися, готуючи матеріал? Чим запам’ятався урок? Де можна застосувати здобуту інформацію?

Домашнє завдання Повторити теоретичний матеріал: п. 12 – 15 №15.2 (5), сторінка 150, № 4, 10, 13.