Урок "Длина окружности. Длина дуги окружности"

Тема: Длина окружности. Длина дуги  окружности.

Цель урока: 

Образовательная: ввести формулу, выражающую длину окружности через ее радиус; ввести формулу для вычисления длины дуги окружности; закрепить знание формул при решении задач.
Развивающая: развивать умение лаконично излагать свои мысли, умение выбирать правильное решение, анализировать и делать выводы; развитие вычислительных навыков, самостоятельности, ответственности.

Воспитательная: воспитание у учащихся интереса к предмету, доброжелательности, умения выслушивать ответы товарищей.

Тип урока: усвоение новых знаний, умений, навыков

 

Оборудование: Доска, линейка, циркуль, цветные мелки, нитки и круги из картона, пластмассы, цилиндрические фигуры различного диаметра, презентация, карточки с заданиями.

Девиз: Ум заключается не только в знаниях,  но и в умении применять знания на деле.

Аристотель

Ход урока

I. Организационный момент.

 – Доброе  утро, друзья мои! Садитесь, пожалуйста.    

 -  Начинаем наш урок.       

-  Слово урок. Такое привычное для нас, но очень весомое. Сколько слов можно  образовать из его букв. И все эти слова нужны нам будут для успешной работы на уроке. 

Интерактивный Метод – «Микрофон»     

- Составим небольшой словарик. Например, улыбка, внимание, успех. Продолжите. 

У – успех, уверенность  

Р – радость, работа  

О – одаренность, организованность  

К – коллективизм, коммуникабельность

Надеюсь что на уроке на  нас ожидает   успех.

II. Актуализация опорных знаний учащихся (повторение теоретического материала):

Игра «Верю – не верю» (методический прием).

В алгебре высказываний (основы логики) истинному высказыванию ставится в соответствие «1», а ложному «0». После выполнения этого задания у вас должно получиться число. Вот и вы, если считаете, что утверждение верное ставите 1, если ложное – 0. И заносите свои ответы в таблицу.
 

1.  Геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки, называется кругом. (-) (называется окружностью)
2. В любой прямоугольник можно вписать окружность. (-)
3. Угол с вершиной в центре окружности называется вписанным углом. (-)

(Угол с вершиной в центре окружности называется ее центральным углом.)

4. Любой треугольник является правильным, если все его углы равны.(+)
5. Около любого правильного многоугольника можно описать окружность и притом только одну. (+)
6. Угол с вершиной в центре окружности называется центральным углом.(+)
7. Любой четырехугольник с равными сторонами является правильным. (-) (добавить и равными углами)
8. Угол, вершина которого лежат на окружности, а стороны пересекают окружность называется ее центральным углом (-)(Угол, вершина которого лежат на окружности, а стороны пересекают окружность, называется вписанным углом.)
9. Многоугольник является правильным, если все его углы равны. (-). (добавить и стороны равны)
10.       Окружность, вписанная в правильный многоугольник, касается каждой стороны многоугольника в его середине. (+).
11.       Окружность, касающаяся всех сторон многоугольника, называется вписанной. (+)

Если все вершины многоугольника лежат на окружности, то окружность называется описанной. (+)

1	2	3	4	5	6	7	8	9	10	11	12
0	0	0	1	1	1	0	0	0	1	1	1

 

III. Мотивация

Чем измерить отрезок? Линейкой.

А чем измерить длину окружности? Нет такого прибора.

А если нет такого прибора, то научимся вычислять длину окружности.
 

ІV. Изучение нового материала

Еще в древности люди пытались решить задачу «Как же измерить длину окружности»?  Ведь окружность является кривой линией, а измерить ее длину с помощью линейки, как это делается при измерении отрезков, невозможно. А знать длину окружности просто необходимо во многих отраслях промышленности и строительства: при изготовлении различных труб, цистерн, поршней; при разметке беговой дорожки на стадионе и т. д.

В 6 классе при изучении темы «Окружность» мы делали следующий опыт: круглый стакан ставили на лист бумаги и обводили его карандашом. На бумаге получится окружность.  Если «опоясать» стакан ниткой, а потом распрямить её, то длина нитки будет приблизительно равна нарисованной окружности.

Вот и мы сейчас с вами вспомним, как мы это делали и будем заполнять таблицу

	Длина окружности	диаметр	отношение
Учитель	25,1 см	8	3,1375
ученик
ученик
ученик

 

Практическая работа. (Работа в парах)

У вас на столах цилиндры разного диаметра, круги из картона, пластмассы. Как измерить длину окружности?

Ответы: 1. Наложить ниточку по контуру круга, а затем измерить ее длину линейкой.

2. Обмотать нить вокруг цилиндра.

Учитель: Правильно. Для нашего эксперимента удобней взять цилиндр, обмотать ниткой и измерить ее длину: 

1. Найдите длину своей окружности.
2. Обозначим длину окружности буквой С.
3. Запишите, чему равна длина вашей окружности.
4. Найдите, чему равен диаметр вашей окружности.
5. При помощи своих смартфонов найдите отношение    Округлите результат  до сотых.
6. Если вы все измерения сделали правильно, то должны получить
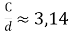
7. Отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой

 

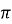
Число «Пи» относится к числам, точное значение которых записать невозможно ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам для наших вычислений достаточно использовать значение π,
округленное до разряда сотых π ≈ 3,14…

8. Выразим С.     С=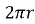. Это и есть формула, по которой находится длина окружности

 

V. Из истории

Проектная работа ученика (презентация о числе π)

Описание:  слайд 1

π3,14159265358979323846264338…

 

 

 

 

 

 

 

слайд 2

Число  π - это число,

которое равно отношению длины окружности к ее диаметру

 

 

 

 

 

 

 

слайд 3

История числа  начинается с египетского папируса 2000 г. до нашей эры.

 

 

 

 

 

 

 

слайд 4

"Двадцать две совы скучали

На больших сухих суках.

Двадцать две совы мечтали

О семи больших мышах"

 

 

слайд 5

Архимед доказал, что число  одинаково для любого круга.

 

 

 

 

 

 

 

 

слайд 6

Погоня за знаками

Мировой рекорд относительно запоминания числа π установил 17 июня 2009 года украинский нейрохирург, доктор медицинских наук, профессор

Андрей Слюсарчук, который

удержал в памяти 30 миллионов

чисел после запятой, – это

практически 20 томов текста.

 

 

слайд 7

Мистика числа
 

 

слайд 8

Скороговорка для запоминания числа

1. Что я знаю о кругах" ( 3,1416).

2. "Это я знаю и помню прекрасно - "Пи" многие знаки мне лишни, напрасны" (3,14159265358)

3. "Учи и знай в числе известном за цифрой цифру, как удачу, примечать" (3,14159265358).

 

 

слайд 9

День рождения числа

Неофициальный праздник «День числа Пи» отмечается 14 марта, которое в американском формате дат (месяц/день) записывается как 3.14, что соответствует приближённому значению числа пи

Эта дата совпала с днем рождения Альберта Эйнштейна –

выдающегося ученого

ХХ столетия.

Праздник числа π придумал в 1987 году физик из Сан-Франциско Ларри Шоу, который обратил внимание на то, что 14 марта (в американском написании - 3.14) ровно о 01:59 даты и время совпадут с первыми разрядами числа π - 3,14159.

 

слайд 10

Праздник числа

Главная церемония проходит в музее. Кульминация приходится на 1 час 59 минут 26 секунд после полудня. Участники праздника маршируют вдоль стен круглого зала, распевая песни о числе, а потом едят круглые пи-роги и пи-ццу, пьют на-пи-тки и играют в игры, которые начинаются на Пи-. В центре зала размещают латунную тарелку, на которой выгравировано число  с первыми 100 знаками после запятой.

 

 

слайд 11

Музей искусств в Сиэтле построен на ступеньках перед зданием музея искусств 
 

 

Так как мы изучаем многоугольники, то рассмотрим следующую задачу

У вас на партах карточки с изображениями окружностей разных диаметров.

 

Задача 1.

1. Впишите в окружность четырехугольник
2. Впишите в окружность восьмиугольник
3. Впишите в окружность шестнадцати угольник

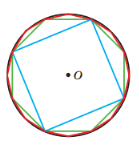После каждого выполнения задания учитель показывает карточки с изображениями.

Какой можно сделать вывод?

А как найти периметр многоугольника?

С увеличением числа сторон многоугольника, периметр многоугольника все меньше и меньше отличается от длины окружности.

Т.е     C = P

Задача 2.

Рассмотрим два правильных n-угольника со сторонами a_n и  a_n′

вписанных в окружности, радиусы которых равны R и R′ соответственно. Тогда их периметры P_n и  P_n ′ можно вычислить по формулам.

Вспомним, как найти периметр многоугольника и радиус  описанной окружности правильного n-угольника (формулу записать  на доске) 

        

 

 

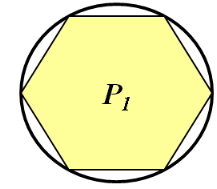
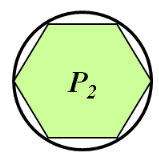
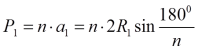
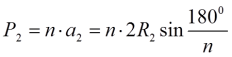
Найдем отношение периметров

 

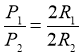
При сокращении получим:

 

Т.к. периметр многоугольника все меньше и меньше отличается от длины окружности, т.е

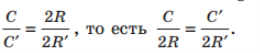
Последнее равенство мы получили при решении задачи 1:

для всех окружностей отношение длины окружности к диаметру является одним и тем же числом.        .

 

Отсюда     C = 2R

 

Покажем, как применяются данные формулы при решении конкретных задач

ЗАДАЧА. Чтобы определить диаметр ствола дерева, лесник измерил длину окружности ствола дерева. Она равна 3,3 м. Каков диаметр ствола дерева. Запишите, что нам известно

Дано: С = 3,3 м                   Решение

Найти: D = ?              C = 2R или     С = D

   D =       D = 1,05 м

Ответ: 1,05м

Перед вами карточка с заданием 1

Заполните таблицу

R	5	10
D			20
C				62.8

 

Физминутка.

Динамическая пауза. ( Направлена на профилактику остеохондроза.)

Сесть на краешек стула.

Поднять руки, потянуться, напрячь мышцы.

Вытянуть руки перед грудью, потянуться.

Руки в стороны, потянуться, напрячь мышцы.

Обхватить себя руками, выгнуть спину.

Принять рабочее положение.

 

ДЛИНА ДУГИ ОКРУЖНОСТИ

Если мы на окружности возьмем какую-то точку и эта точка сделает полный оборот по этой окружности, то мы с вами получим угол в 360⁰.

Найдем формулу для вычисления длины дуги окружности с градусной мерой n°. Т.к. градусная мера всей окружности равна 360°, то длина дуги в 1° равна

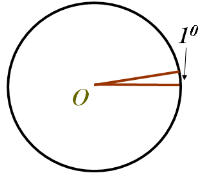       l =  =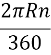

V. Решение задач на закрепление материала

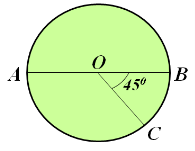Задача 1.

Найти длины дуг ВС и АС,

если АВ = 10 см

 

Решение:

1. Дуга ВС:  l = =

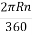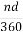
ВС =

2. Дуга  АС = АВ - ВС:
   С = 3,14 • 10 = 31,4
   дуга АВ =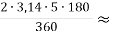 15,

АОС = 180⁰ - < ВОС = 180⁰ – 45⁰ = 135⁰

     АС  =      11,8

Для проверки

Т.К. < АОС = 3 ٠ <ВОС, то длина дуги АС тоже в 3 раза больше длины дуги АС.

Т.е   Дуга АС = 3٠3,925 = 11,775 11,78

VІ. Самостоятельная работа учащихся.

ТЕСТ.

I вариант	IІ вариант
1. Диаметр больше радиуса в …      а) 2 раза;       б) π  раз;      в). 2π  раз 2. Длина окружности больше радиуса в …      а) π  раз;         б) 2π  раз;           в) 2 раза. 3. Чему равна длина окружности, если ее диаметр равен 10 см?      а)  10π  см;       б)  π  см;      в) 20π  см.	1.Радиус окружности меньше диаметра  в … а) 2π  раз;     б) 2 раза;        в) π  раз 2.Длина окружности больше диаметра в …      а) 2π  раз;         б) π  раз;           в) 2 раза. 3. Чему равна длина окружности, если ее радиус равен 10 см?      а)  10π  см;       б)  π  см;      в) 20π  см

 

Затем – взаимопроверка.

 I вариант:   а  б  а   

  II вариант:  б   б  в

VІІ. Итоги урока. Рефлексия. Д/з. На листочках поставьте:

1 – если на уроке вам было интересно и понятно;

2 – интересно, но не понятно;

3 – не интересно, но понятно;

4 – не интересно, не понятно.

Д/з: § 2. п. 7. ( до Выведем формулу для площади круга…)

Решить №7.2; 7.7;  7.9; 7.16

Дополнительно. Отгадать загадку: Этот предмет изобрел очень талантливый юноша, который придумал гончарный круг, первую в мире пилу. Под пеплом Помпеи археологи обнаружили много таких предметов, изготовленных из бронзы. В Древней Греции умение пользоваться этим предметом считалось верхом совершенства, а уж умение решать задачи с его помощью - признаком высокого положения в обществе и большого ума. Самый древний этот предмет пролежал в земле 2000 лет, но конструкция его за сотни лет не изменилась. Что это?

 

Окончен урок, и выполнен план.

Спасибо, ребята, огромное вам.

За то, что упорно и дружно  трудились,

И знания точно уж вам пригодились.