Урок "Загальне рівняння прямої"

Тема уроку:  Загальне рівняння прямої на площині

Цілі уроку:  Вивести загальне рівняння прямої на площині. Формувати вміння застосовувати загальне рівняння прямої для розв’язування задач.

Розвивати увагу, логічне мислення, пам’ять, дослідницькі навички, вміння узагальнювати та робити висновки

Виховувати загальну математичну культуру, культуру математичної мови і письма

Тип уроку:  урок нових знань

Обладнання:  мультимедійний комплекс, комп’ютерна  презентація Power Point

ХІД УРОКУ:

Слайд 1

1. Організація класу
2. Актуалізація опорних знань

Питання класу:

Слайд 2

1. Відстань між точками А(х₁; у₁) и В (х₂; у₂) можна знайти за формулою
2. Якщо точка М (х; у) є серединою відрізка АВ с кінцями в точках А (х1; у1) і               В (х2; у2), то її координати можна знайти за формулами

Слайд 3

3. Рівняння кола
4. Загальний вигляд рівняння з двома змінними
5. Назвіть коефіцієнти а, b и с в рівнянні
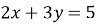
6. Яка з пар чисел (2; 3), (1;1) є розв’язком даного лінійного рівняння з двома змінними?
7. Яка фігура є графіком лінійного рівняння з двома змінними?

Слайд 4 Проблемне питання: Чи можу я стверджувати, що будь-яке рівняння з двома змінними є загальним рівнянням прямої? Відповідь на це питання ми з вами отримаємо трошки пізніше

Слайд 5 Відкрийте зошити, запишіть число, класна робота і тему сьогоднішнього уроку «Загальне рівняння прямої на площині»

3. Пояснення нового матеріалу

 Слайд 6

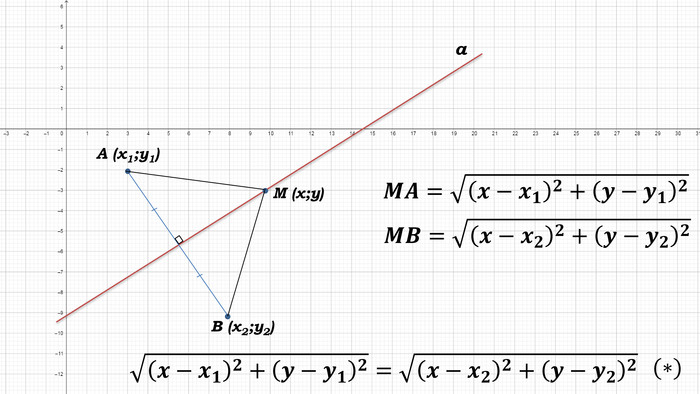
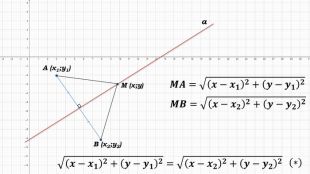
Нехай а – задана пряма. Оберемо точки А (х1; у1) и  В (х2; у2) такі, щоб пряма а була серединним перпендикуляром відрізка АВ. В якому випадку точка М (х; у) буде належати прямій а? (Якщо МА = МВ, тобто точка М буде рівновіддалена від кінців відрізку АВ)

Знайдемо відстані МА и МВ.

; .

Так як МА = МВ, то . Тобто рівняння (*) є рівнянням прямоі а.

Але з курсу алгебри 7-го класу ми знаємо, що рівняння прямої має значно простіший вигляд, а саме ах + bу = с, де а,  b и с – деякі числа, причому а и b одночасно не дорівнюють 0.

Слайд 7 Покажемо, що рівняння (*) можна привести до вигляду ах + bу = с. Піднесемо обидві частини рівняння (*) в квадрат:  .

Розкриємо дужки та зведемо подібні доданки:

.

Позначивши  отримаємо рівняння ах + bу = с.

Слайд 8 Загальне рівняння прямої

Чи можуть коефіцієнти а, b и с дорівнювати нулю? Якщо так, то що ми отримаємо? Слайд 9

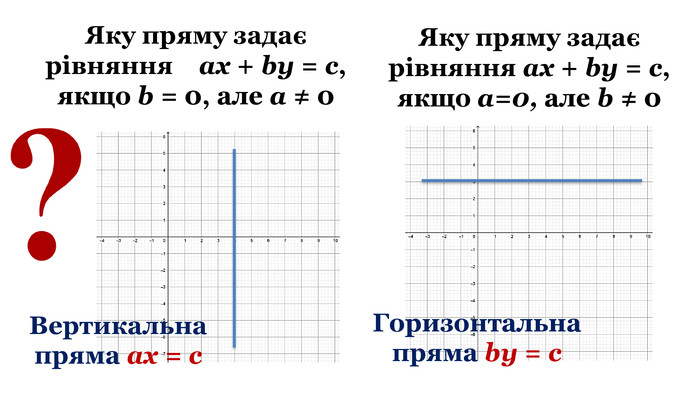
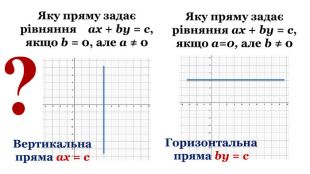
1. Яку пряму задає рівняння ах + bу = с, якщо b = 0 , але а ≠ 0 (вертикальну пряму)
2. Яку пряму задає рівняння ах + bу = с, якщо а = 0, але  b ≠ 0 (горизонтальну пряму)

Слайд 10 Відкрийте, будь ласка, підручник на сторінці 98 и знайдіть відповідь на запитання:

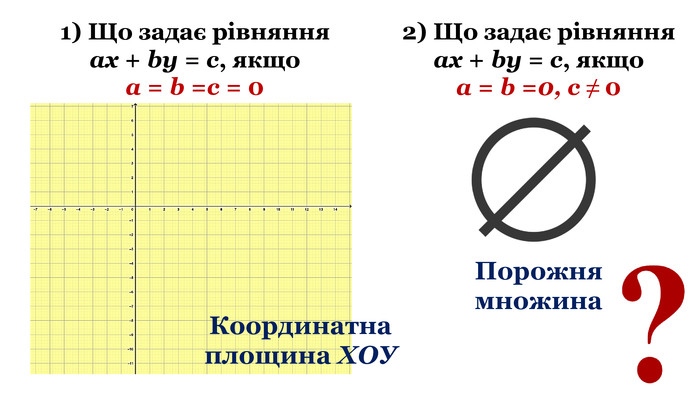
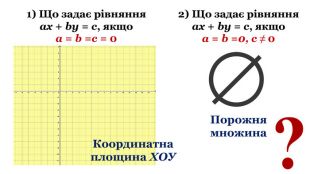
1. Що задає  рівняння ах + bу = с, якщо а = b =с = 0
2. Що задає рівняння ах + bу = с, якщо а = b = 0, с ≠ 0

Слайд 11 Висновок: Будь-яке рівняння вигляду ax + by = c, де а, b и с – деякі числа, причому а и b одночасно не дорівнюють 0, є  загальним рівнянням прямої

Слайд 12 В залежності від коефіцієнтів а, b, c отримаємо наступне розміщення прямої в системі координат

Питання: А яким ще, відомим вам рівнянням, можна пряму на площині? (у = kх + b). Так, але це тема нашого наступного уроку

4. Розв’язування задач

Слайд 13

№ 11.1 Знайдіть координати точок перетину прямої 4х – 5у = 20 з осями координат. Чи належать точки А (10; 4) и В (6;1) даній прямій ?

Слайд 14

№ 11.6 Складіть рівняння прямої, яка проходить через точки:

1. А (1; ‒3) и В (‒2; ‒9)

Слайд 15 Для полегшення розв᾽язку № 1 даної задачі я підготувала алгоритм розв᾽язання, але деякі дані в неї пропущені. Вам потрібно заповнити пропуски в ході розв᾽язку задачі

1. Рівняння даної прямої будемо шукати у вигляді ax + by = c.

2. Так як  координати точок А і В задовольняють рівнянню шуканої прямої, маємо систему рівнянь

Помножимо перше рівняння системи на 2 та додамо обидва рівняння. Маємо:

Підставимо отриманий вираз в перше рівняння системи: ,

Замінимо в рівнянні ax + by = c коефіцієнти а и с відповідними виразами. Отримаємо: ,

Шукане рівняння прямої

Слайд 16

2) С (3; 5) і D (3;‒10)

Точки С і D  мають однакові абсциси, тому шукана пряма паралельна осі Оу і має вигляд  х = 3.

3) Е (‒ 4; ‒1) и F (9; ‒ 1)

Точки Е і F мають однакові ординати, тому шукана пряма паралельна осі Ох і має вигляд  у = ‒1.

Слайд 17

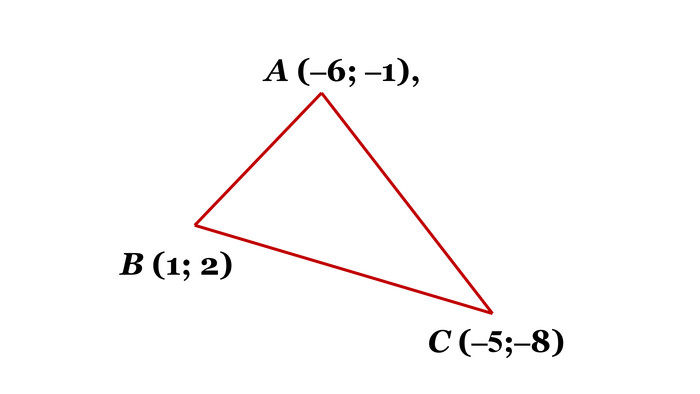
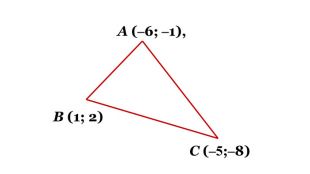
№ 11.8 Точки А (‒6; ‒1), В (1; 2) и С (‒5;‒8) – вершини трикутника АВС. Складіть рівняння прямої, яка містить медіану АК трикутника

Слайд 18 Зробимо малюнок

Так як АК – медіана трикутника АВС, то ВК = СК. Тому К – середина відрізка АК. Знайдемо координати середини відрізка:

  K (‒2; ‒3)

Складемо рівняння прямої, яка проходить через точки А (‒6; ‒1) и K (‒2; ‒3)

Подставимо отриману рівність в перше рівняння системи: .

Подставимо отримані вирази у загальне рівняння прмої. Маємо:

Поділимо обидві частини рівняння на  а (а ≠ 0).

Отримаємо – шукане рівняння прямої

Слайд 19  

11.14 Доведіть, що коло   і пряма перетинаються, та знайдіть координати точок їх перетину

Припустимо, що коло та пряма перетинаються. Тоді вони мають дві спільні точки. Для знаходження їхніх координат складемо та розв’яжемо систему координат:

Розв᾽яжемо друге рівняння системи:

   Відповідь: (2; 5), (5; 2)

5. Підсумки уроку

1. Що ми вивчили на сьогоднішнім уроці?
2. Який вигляд має  загальне рівняння прямої на площині?
3. Яким ще рівнянням можна задати пряму на площині?
4. Чи будь-яке рівняння з двома змінними є рівнянням прямої?

Слайд 20

6. Домашнє завдання §11,  № 11.9, 11.12, 11.15