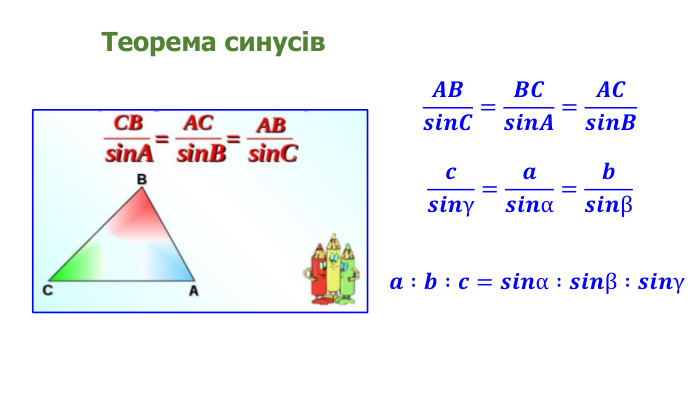
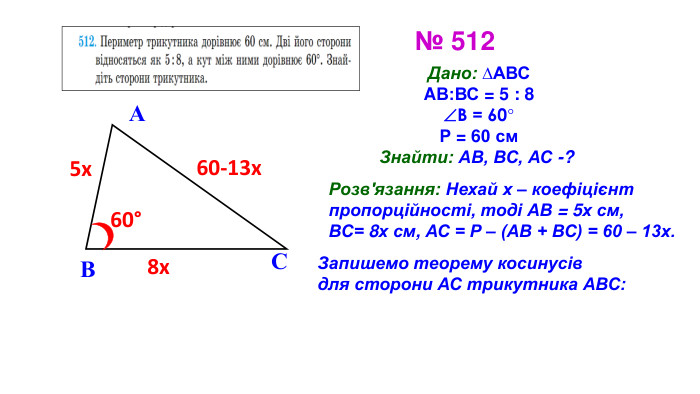
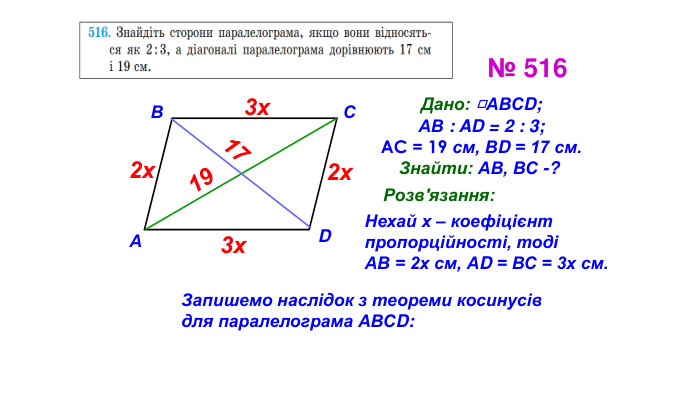
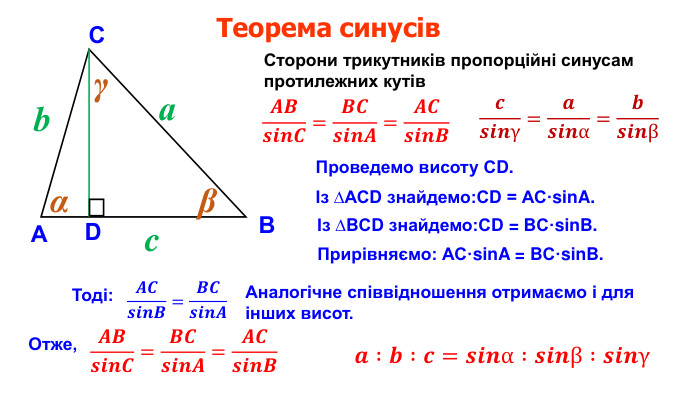
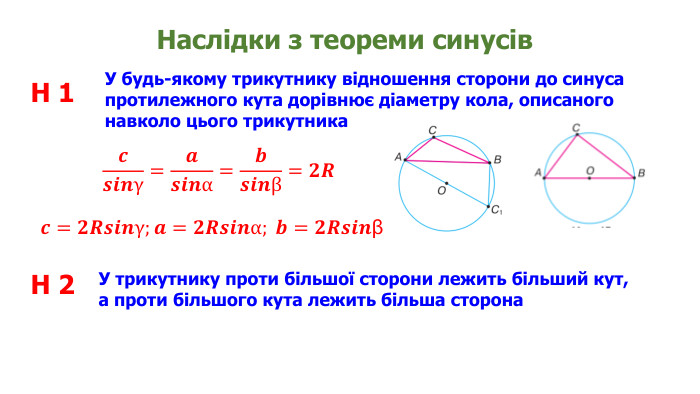
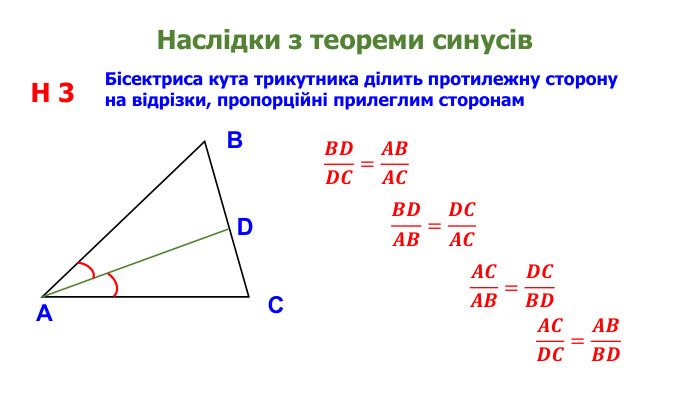
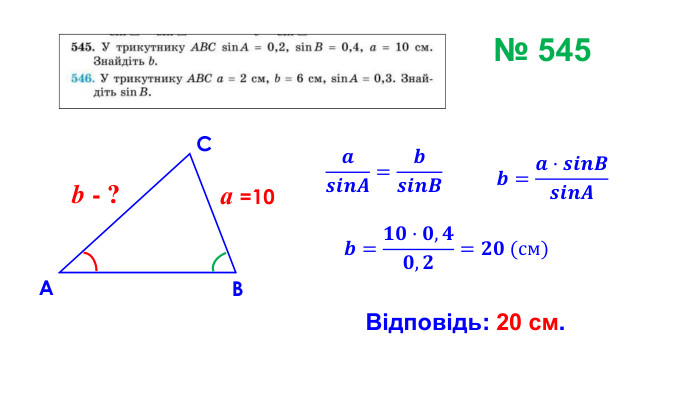
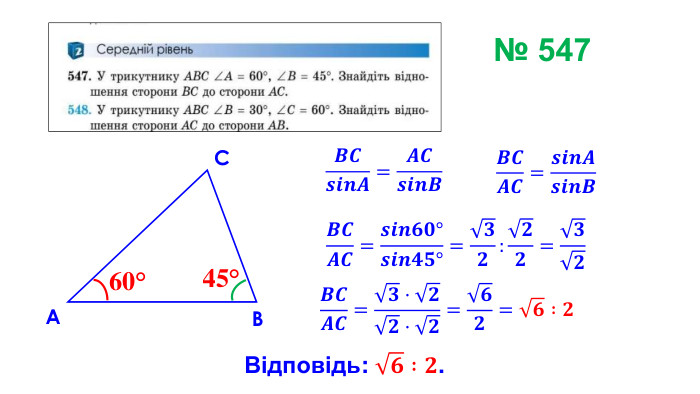
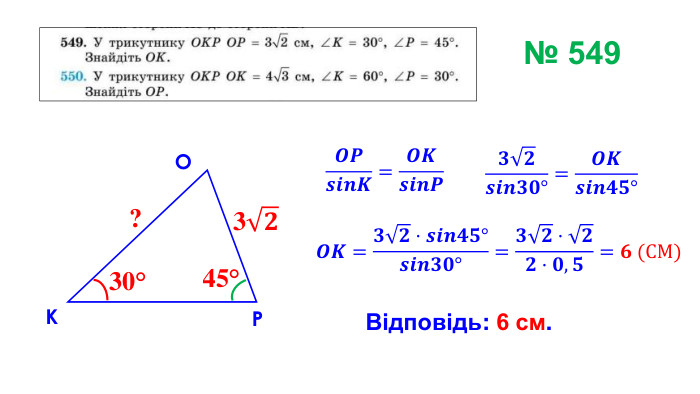
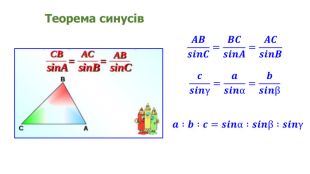
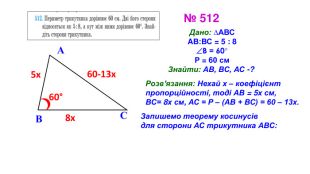
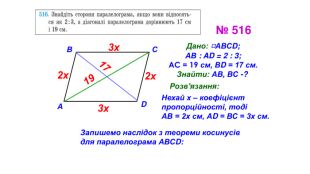
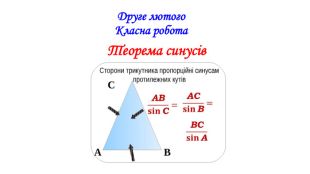
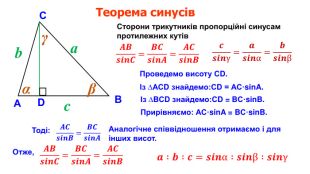
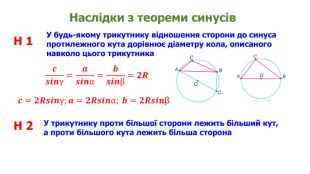
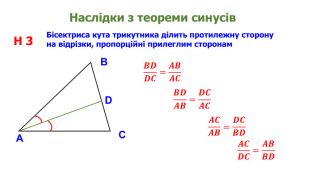
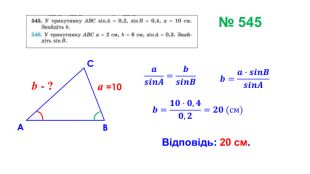
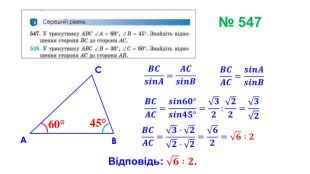
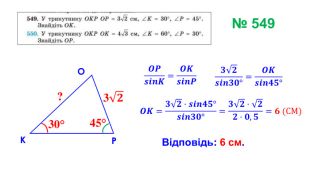
Презентація "Теорема синусів"
Про матеріал
Презентація призначена для проведення уроку геометрія в дистанційному форматі у 9 класі за підручником О. С. Істер (2017). Містить елементи анімації, що дуже зручно при проведені уроку вчителем і спілкуванні з дітьми. Матеріал підібраний у логічній послідовності. Є перевірка домашньої роботи, теоретична частина, класна робота. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку