Урок " Ознаки паралельності прямих"

Конспект уроку

 

7Г     Тема уроку:  Паралельні прямі

                      Ознаки   паралельності прямих.

.

Мета: закріпити знання учнів про ознаки паралельності двох прямих (за кутами, що утворилися при перетині даних прямих січною). Сформувати вміння:

• визначати вид двох кутів, що утворилися при перетині двох прямих
  січною;
• за певним співвідношенням цих кутів робити висновок щодо паралельності прямих;
• для встановлення співвідношення кутів використовувати знання про
  властивості кутів (вертикальних, суміжних, при основі рівнобедреного
  трикутника).

Тип уроку: застосування знань, засвоєння вмінь та навичок.

Ознаки паралельності прямих

1.Якщо при перетині двох прямих січною відповідні кути рівні, то прямі паралельні.

 

 

 

 

 

 

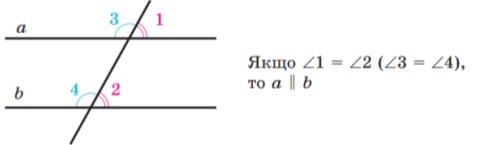
2. Якщо при перетині двох прямих січною сума внутрішніх односторонніх

кутів дорівнює 180°, то прямі паралельні.

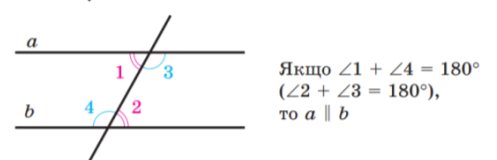
3. Якщо при перетині двох прямих січною внутрішні різносторонні кути рівні , то прямі паралельні.

 

 

 

 

 

 

 

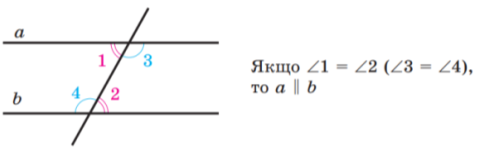
Розв’язання задач

Задача 1.

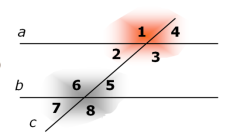
    Дано:

    ;  

     с – січна

   

   Знайти: 

 

Розв’язання.

за умовою;

як вертикальні , тоді

як відповідні , тоді ;

за властивістю суміжних кутів, тоді

;

Відповідь:;

 

Задача 2. Усно

 

На якому малюнку прямі а і b паралельні?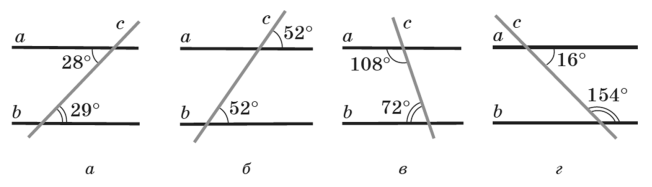

Задача 3.

    Дано:

    ;  

     с – січна

   

   Знайти:  ,

 

Розв’язання.

за умовою

Введемо коефіцієнт пропорційності х, тоді

, тоді

за властивістю внутрішніх односторонніх кутів, тоді

складемо і розв’яжемо рівняння:

- коефіцієнт

Звідси  , а  .

як відповідні , тоді ;

Відповідь: ,   ,  ;

 

Задача 4.

    Дано:

    ;  

     с – січна

   

   Знайти:  ,

 

Розв’язання.

Нехай , тоді

за властивістю внутрішніх односторонніх кутів, тоді

складемо і розв’яжемо рівняння:

Звідси  , а  .

як внутрішні різносторонні , тоді .

Відповідь:,   , .

 

Задача 5.

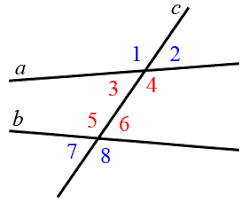
    Дано:

    ;  

     с – січна

   

   Довести :   ;  

 

 

 

 

Доведення

За умовою.

за властивістю суміжних кутів

і відповідні кути. А якщо відповідні кути  рівні, то    паралельні.

 

 

Задача 6.

    Дано:

    ;  

     с – січна

   

більше 

 

   Довести :   ;  

 

 

Доведення

  За  властивістю вертикальних кутів

За за властивістю вертикальних кутів

внутрішні односторонні кути .

А якщо  внутрішні односторонні кути в сумі дорівнюють   то   паралельні.

Задача 7.

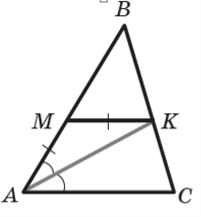Дано: АК – бісектриса

∠ВАС, АМ=МК;

Довести: МК∥АС.

Доведення

Так як АК – бісектриса ∠ВАС, то ∠МАК=∠САК.

Так, як АМ=МК, то  - рівнобедрений з основою АК. Тоді

Отже, ∠САК=∠МКА

∠САК і ∠МKА різносторонні при прямих МК і АС та січній АК.

Отже, за ознакою паралельності прямих МК∥АС.

 

Домашнє завдання