Презентація "Тотожні перетворення виразів,які містять кавдратні корені"
Про матеріал
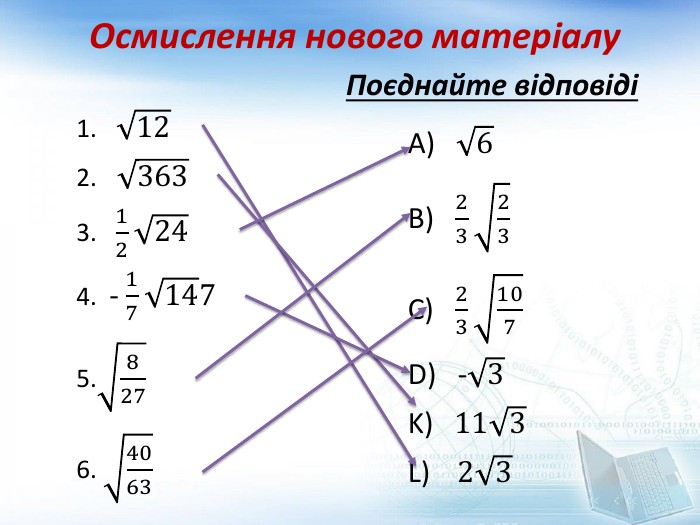
Дана презентація ознайомлює учнів із такими перетвореннями : - винесення множника з під знака кореня, - внесення множника під знак кореня, приведення подібних радикалів. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку






![Винесення множника з-під знака кореня. Приклад. 𝟕𝟓 = 𝟐𝟓⋅𝟑= 𝟐𝟓⋅𝟑=𝟓𝟑(розклали число 75 на множники, один з яких є квадратом числа, і застосували теорему про корінь з добутку); 𝒂𝟕=𝒂𝟔⋅𝒂=𝒂𝟔⋅𝒂=[ а 3 ]𝒂. (подали вираз а7 у вигляді добутку двох степенів, один з яких має парний показник, скористалися теоремами про корінь з добутку , корінь зі степеня і тим фактом, що 𝒂𝟕 має змість для 𝑎≥0, отже [𝒂𝟑] = 𝒂𝟑. Винесення множника з-під знака кореня. Приклад. 𝟕𝟓 = 𝟐𝟓⋅𝟑= 𝟐𝟓⋅𝟑=𝟓𝟑(розклали число 75 на множники, один з яких є квадратом числа, і застосували теорему про корінь з добутку); 𝒂𝟕=𝒂𝟔⋅𝒂=𝒂𝟔⋅𝒂=[ а 3 ]𝒂. (подали вираз а7 у вигляді добутку двох степенів, один з яких має парний показник, скористалися теоремами про корінь з добутку , корінь зі степеня і тим фактом, що 𝒂𝟕 має змість для 𝑎≥0, отже [𝒂𝟑] = 𝒂𝟑.](/uploads/files/45132/333251/374584_images/6.jpg)