Презентація: Тригонометрія навколо нас



















 sinx і одночасно y<- sinx; потім зафарбовуємо області, де y< sinx і одночасно y>- sinx. Цій нерівності задовольнятимуть області,зафарбовані на рис.2. " title="Математичні орнаменти1. Системі нерівностей задовольняють координати точок, які лежать одночасно вище за синусоїду ( для них у>sinx) і нижче кривої y=-sinx, тобто " область рішень" системи складатиметься із зафарбованих на рис.1 областей. 2. Розглянемо нерівності 1)(y - sinx) (y sinx)<0. Для вирішення цієї нерівності спочатку будуємо графіки функцій : y=sinx; y=-sinx. Потім зафарбовуємо області, де y>sinx і одночасно y<- sinx; потім зафарбовуємо області, де y< sinx і одночасно y>- sinx. Цій нерівності задовольнятимуть області,зафарбовані на рис.2. ">
sinx і одночасно y<- sinx; потім зафарбовуємо області, де y< sinx і одночасно y>- sinx. Цій нерівності задовольнятимуть області,зафарбовані на рис.2. " title="Математичні орнаменти1. Системі нерівностей задовольняють координати точок, які лежать одночасно вище за синусоїду ( для них у>sinx) і нижче кривої y=-sinx, тобто " область рішень" системи складатиметься із зафарбованих на рис.1 областей. 2. Розглянемо нерівності 1)(y - sinx) (y sinx)<0. Для вирішення цієї нерівності спочатку будуємо графіки функцій : y=sinx; y=-sinx. Потім зафарбовуємо області, де y>sinx і одночасно y<- sinx; потім зафарбовуємо області, де y< sinx і одночасно y>- sinx. Цій нерівності задовольнятимуть області,зафарбовані на рис.2. ">
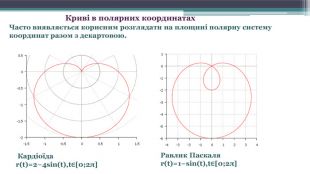
![Криві в полярних координатах Часто виявляється корисним розглядати на площині полярну систему координат разом з декартовою. Кардіоїда r(t)=2−4sin(t),t∈[0;2π]Равлик Паскаляr(t)=1−sin(t),t∈[0;2π] Криві в полярних координатах Часто виявляється корисним розглядати на площині полярну систему координат разом з декартовою. Кардіоїда r(t)=2−4sin(t),t∈[0;2π]Равлик Паскаляr(t)=1−sin(t),t∈[0;2π]](/uploads/files/374096/239724/259223_images/29.jpg)
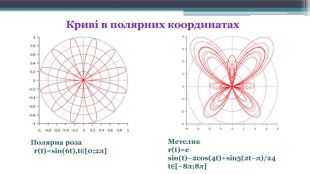
![Полярна роза r(t)=sin(6t),t∈[0;2π] Метеликr(t)=e sin(t)−2cos(4t)+sin5(2t−π)/24 t∈[−8π;8π] Криві в полярних координатах Полярна роза r(t)=sin(6t),t∈[0;2π] Метеликr(t)=e sin(t)−2cos(4t)+sin5(2t−π)/24 t∈[−8π;8π] Криві в полярних координатах](/uploads/files/374096/239724/259223_images/30.jpg)





Тригонометрія - це розділ математики, що вивчає тригонометричні функції. Складно уявити, але з цією наукою ми стикаємося не лише на уроках математики, але і в нашому повсякденному житті. Тригонометрія зустрічається в таких науках, як фізика, біологія, не останню роль вона грає і в медицині, і, що найцікавіше, без неї не обійшлося навіть в музиці і архітектурі. Слово тригонометрія уперше з'являється в 1505 році в заголовку книги німецького математика Питискуса. Тригонометрія - слово грецьке, і у буквальному перекладі означає вимір трикутників ( trigonan - трикутник, metreo - вимірюю).
Мета моєї роботи : дослідити історію розвитку тригонометрії і перспективу багатогранності її застосування,графічні можливості тригонометричних функцій. Завдання:1. Простежити походження тригонометрії, символів і термінів, розглянути шлях розвитку тригонометрії.2. Розглянути можливості застосування тригонометрії в реальному житті.3. Розкрити на конкретних прикладах можливості використання тригонометричних функцій, що дозволяють "мало цікаві" функції перетворювати на функції, графіки яких мають дуже оригінальний вигляд. Гипотеза: Тригонометрия дуже важлива і цікава. Більшість фізичних явищ природи, фізіологічних процесів, закономірностей в музиці і мистецтві можна описати за допомогою тригонометрії і тригонометричних функцій. Проблема: навіщо треба вивчати тригонометрію, де можна використати знання, пов'язані з тригонометрією? Чому знання тригонометрії потрібні для сучасної людини?
Одним з основоположників тригонометрії вважають старогрецького астронома Гіпарха, що жив в II ст. до н. э. Саме йому приписують створення тригонометрії як науки, пограничної між геометрією і астрономією. Гіпарх уперше розглянув тригонометричний круг і вичислив таблицю хорд у крузі, що стала основним елементом грецької тригонометрії на площині. ГІПАРХ НІКЕЯГІПАРХ НІКЕЯ(180- 125 д.н.э.)
Велика заслуга у формуванні тригонометрії як окремої науки належить азербайджанському ученому Насір ад-Діну Мухаммаду ат-Тусі (1201-1274), що написав "Трактат про повний чотирикутник", в якому містяться практичні способи рішення типових завдань. Твір ат-Тусі став широко відомий в Європі і істотно вплинув на розвиток тригонометрії. Аль- Хорезмі (783-850 р. н. е)Побудував таблицю синусів и котангенсів. Насір ад-Діну Мухаммаду ат-Тусі (1201-1274)Насір ад-Діну Мухаммаду ат-Тусі Аль- Хорезмі (783-850 р. н.е)
Німецький вчений Йоганн Мюллер, відомий в науці під ім'ям Регіомонтан, видав працю "П'ять книг про трикутники усіх видів", що зіграла важливу роль в розвитку тригонометрії. У ній дано систематичний виклад тригонометрії як самостійної наукової дисципліни. Він узагальнює методи рішення прямокутних трикутників і дає таблиці синусів з точністю до 0,0000001. РЕГІОМОНТАНРегіомонтан (1818—1899)
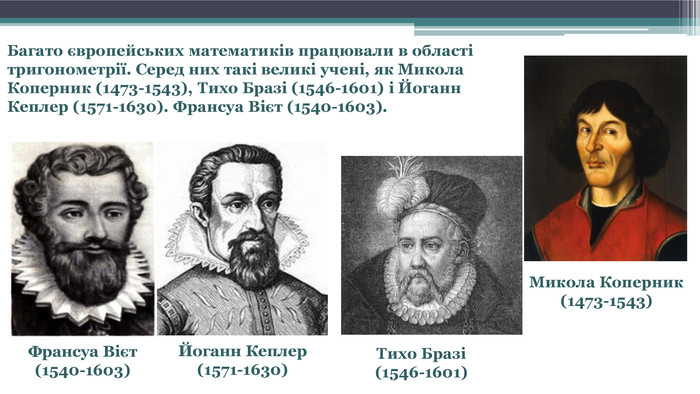
Багато європейських математиків працювали в області тригонометрії. Серед них такі великі учені, як Микола Коперник (1473-1543), Тихо Бразі (1546-1601) і Йоганн Кеплер (1571-1630). Франсуа Вієт (1540-1603). Микола Коперник(1473-1543)Тихо Бразі(1546-1601) Йоганн Кеплер(1571-1630)Франсуа Вієт(1540-1603)
Франсуа Вієт (1540-1603 р.)Франсуа Вієт Франсуа Вієт (1540-1603) доповнив і систематизував різні випадки рішення плоских і сферичних трикутників, відкрив "плоску" теорему косинусів і формули для тригонометричних функцій кратних кутів. Ісаак Ньютон (1643-1727р.)Ісаак Ньютонрозклав функції в ряди і відкрив шлях для їх використання в математичному аналізі
Сучасний вигляд тригонометрія отримала в працях великого вченого Леонарда Ейлера. Ввів поняття функції і прийняту в наші дні символіку. З’ясував питання про знаки всіх тригонометричних функцій довільного аргументу. Цей учений ввів і обернені тригонометричні функції. Ейлерові належить ідея розглядати тригонометричні функції як відношення відповідних ліній до радіусу круга, тобто як числа, при чому радіус круга як "повний синус" він прийняв за одиницю. ЛЕОНАРД ЕЙЛЕРЛеонард Ейлер(1707- 1783)
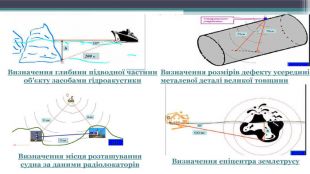
Тригонометричні обчислення застосовуються практично у всіх областях геометрії, фізики і інженерної справи. Велике значення має техніка тріангуляції, що дозволяє вимірювати відстані до недалеких зірок в астрономії, між орієнтирами в географії, контролювати системи навігації супутників. Слід відзначити застосування тригонометрії в наступних областях: техніка навігації, теорія музики, акустика, оптика, аналіз фінансових ринків, електроніка, теорія ймовірностей, статистика, біологія, медицина (включаючи ультразвукове дослідження (УЗД), комп'ютерна томографія, фармацевтика, хімія, теорія чисел, сейсмологія, метеорологія, океанологія, картографія, багато розділів фізики, топографія, геодезія, архітектура, фонетика, економіка, електронна техніка, машинобудування, комп'ютерна графіка, кристалографія.
Тригонометрія в астрономіїПотреба в рішенні трикутників раніше всього виявилася в астрономії; тому, впродовж довгого часу тригонометрія розвивалася і вивчалася як один з розділів астрономії. Складені Гіпархом таблиці положень Сонця і Місяця дозволили передобчислювати моменти настання затьмарень (з помилкою 1-2 г.). Гіпарх уперше став використовувати в астрономії методи сферичної тригонометрії. Учений склав величезний на ті часи каталог положень 850 зірок, розділивши їх по блиску на 6 мір (зоряних величин). Гіпарх ввів географічні координати - широту і довготу, і його можна вважати засновником математичної географії. (ок. 190 до н. э. - ок. 120 до н.е.)
Коливання маятника теж відбуваються за синусоїдальним законом. Де х - значення величини, що змінюється, t - час, А - амплітуда коливань, ω - циклічна частота коливань, (ωt+ φ) - повна фаза коливань, r - початкова фаза коливань. Коливання, при яких зміни величин відбуваються по закону косинуса або синуса( гармонічному закону), називається. Гармонічними коливаннямиx (t) =Asin (ωt+ φ) або x (t) =Acos (ωt+ φ) Графік гармонічних коливань називається синусоїдою, тому в фізиці та техніці самі гармонійні коливання часто називають синусоїдальними коливаннями. Тригонометрія в фізиці
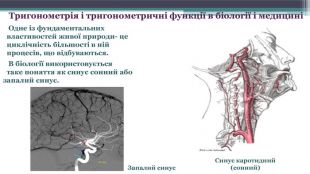
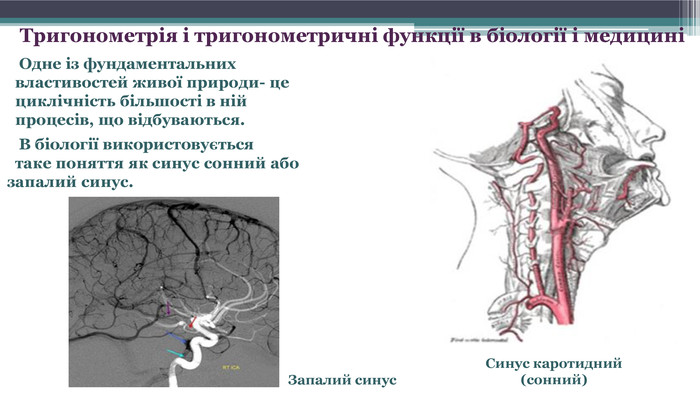
Синус каротидний (сонний) Запалий синус. Тригонометрія і тригонометричні функції в біології і медицині В біології використовується таке поняття як синус сонний або запалий синус. Одне із фундаментальних властивостей живої природи- це циклічність більшості в ній процесів, що відбуваються.
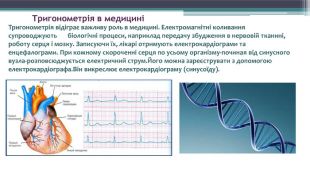
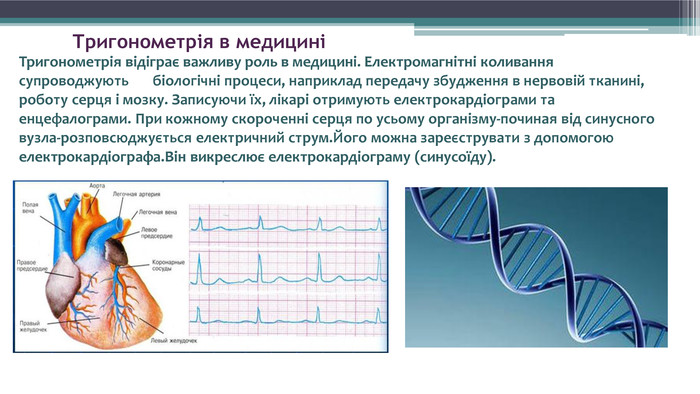
Тригонометрія в медициніТригонометрія відіграє важливу роль в медицині. Електромагнітні коливання супроводжують біологічні процеси, наприклад передачу збудження в нервовій тканині, роботу серця і мозку. Записуючи їх, лікарі отримують електрокардіограми та енцефалограми. При кожному скороченні серця по усьому організму-починая від синусного вузла-розповсюджується електричний струм. Його можна зареєструвати з допомогою електрокардіографа. Він викреслює електрокардіограму (синусоїду).
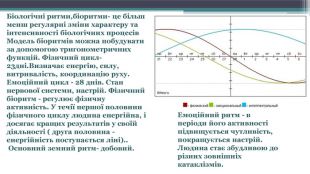
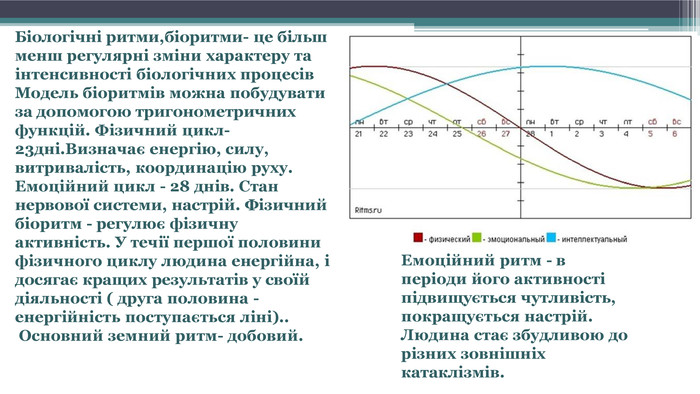
Біологічні ритми,біоритми- це більш менш регулярні зміни характеру та інтенсивності біологічних процесів. Модель біоритмів можна побудувати за допомогою тригонометричних функцій. Фізичний цикл-23дні. Визначає енергію, силу, витривалість, координацію руху. Емоційний цикл - 28 днів. Стан нервової системи, настрій. Фізичний біоритм - регулює фізичну активність. У течії першої половини фізичного циклу людина енергійна, і досягає кращих результатів у своїй діяльності ( друга половина - енергійність поступається ліні).. Основний земний ритм- добовий. Емоційний ритм - в періоди його активності підвищується чутливість, покращується настрій. Людина стає збудливою до різних зовнішніх катаклізмів.
Рух риб у воді відбувається за законом синуса або косинуса, якщо зафіксувати точку на хвості, а потім розглянути траєкторію руху. При плаванні тіло риби набуває форми кривої, яка нагадує графік функції у=tqх. При польоті птаха траєкторія помаху крил утворює синусоїду. Тригонометрія в природі
Періодичний закон Д.І. Менделєєва - одно з найбільших відкриттів закону періодичності властивостей хімічних елементів і утворюваних ними хімічних сполук від атомної маси і заряду ядра атома. Ця система знаходиться в усіх підручниках хімії, усіх учнів різних країн. Період це ряд хімічних елементів, що починається лужним металом і закінчується інертним газом. Тут ми спостерігаємо періодичне змінення - послаблення металевих властивостей, перехід в неметалічні властивості, їх посилення, і період закінчується інертним газом. Періодичність у всьому в живій і неживій природі. Тригонометрія в хімії
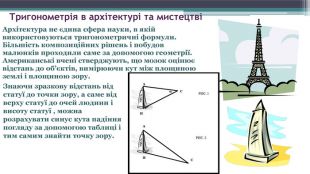
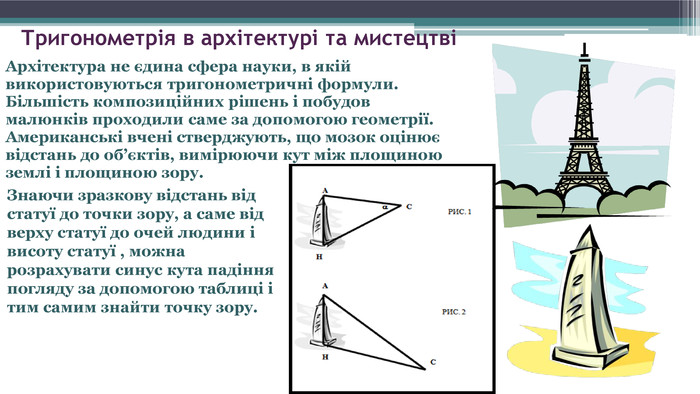
Тригонометрія в архітектурі та мистецтвіАрхітектура не єдина сфера науки, в якій використовуються тригонометричні формули. Більшість композиційних рішень і побудов малюнків проходили саме за допомогою геометрії. Американські вчені стверджують, що мозок оцінює відстань до об’єктів, вимірюючи кут між площиною землі і площиною зору. Знаючи зразкову відстань від статуї до точки зору, а саме від верху статуї до очей людини і висоту статуї , можна розрахувати синус кута падіння погляду за допомогою таблиці і тим самим знайти точку зору.
Антоніо Гауді (1852 - 1926)Великий іспанський архітектор, народився в позаминулому столітті в р. Реусе (Каталонія), автор численних проектів, що відрізняються своєю неповторністю і оригінальністю. Він зробив Барселону несхожою ні на одне інше місто світу. Він вважав, що прямий кут придумали люди, позбавлені фантазії. А зразком досконалості для Гауді було куряче яйце. Особистий стиль архітектора : синтез романо-готичного середньовіччя, органічний натуралізм, східні мотиви, геометризм, модернізм з пануючим культом тієї лінії, що звивається.
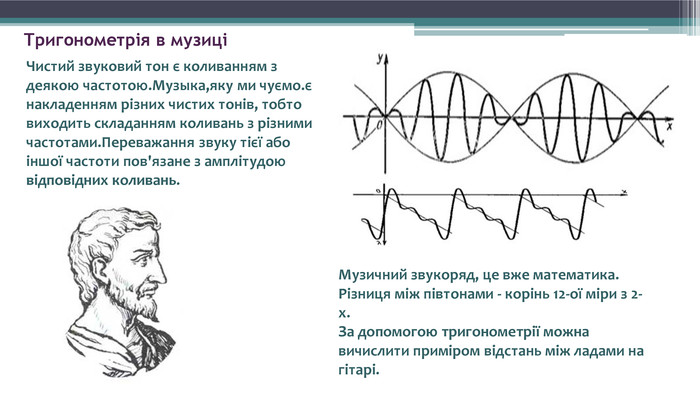
Тригонометрія в музиціЧистий звуковий тон є коливанням з деякою частотою. Музыка,яку ми чуємо.є накладенням різних чистих тонів, тобто виходить складанням коливань з різними частотами. Переважання звуку тієї або іншої частоти пов'язане з амплітудою відповідних коливань. Музичний звукоряд, це вже математика. Різниця між півтонами - корінь 12-ої міри з 2-х. За допомогою тригонометрії можна вичислити приміром відстань між ладами на гітарі.
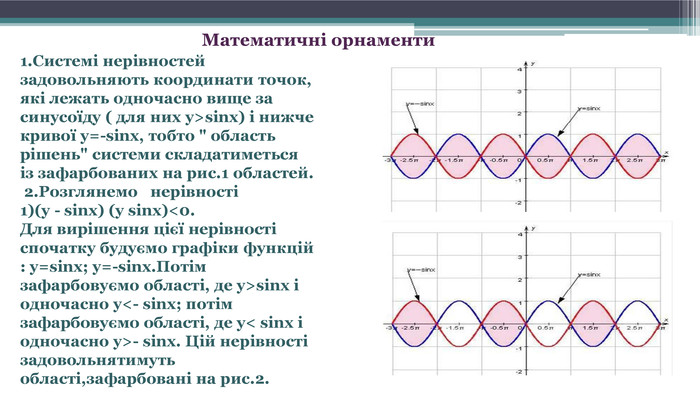
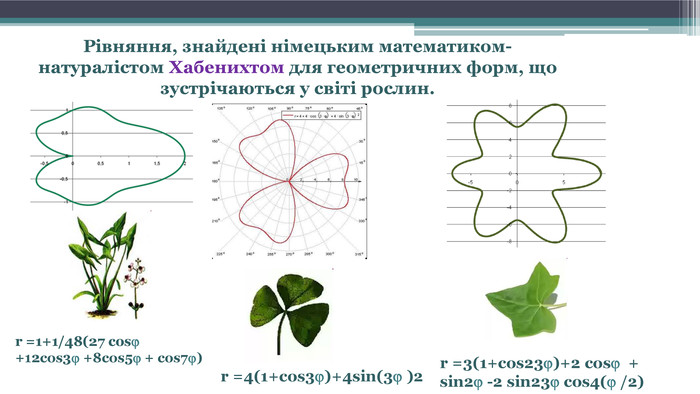
Математичні орнаменти1. Системі нерівностей задовольняють координати точок, які лежать одночасно вище за синусоїду ( для них у>sinx) і нижче кривої y=-sinx, тобто " область рішень" системи складатиметься із зафарбованих на рис.1 областей. 2. Розглянемо нерівності 1)(y - sinx) (y sinx)<0. Для вирішення цієї нерівності спочатку будуємо графіки функцій : y=sinx; y=-sinx. Потім зафарбовуємо області, де y>sinx і одночасно y<- sinx; потім зафарбовуємо області, де y< sinx і одночасно y>- sinx. Цій нерівності задовольнятимуть області,зафарбовані на рис.2.
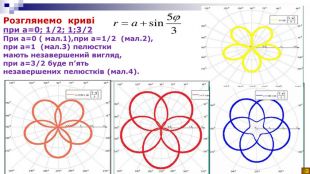
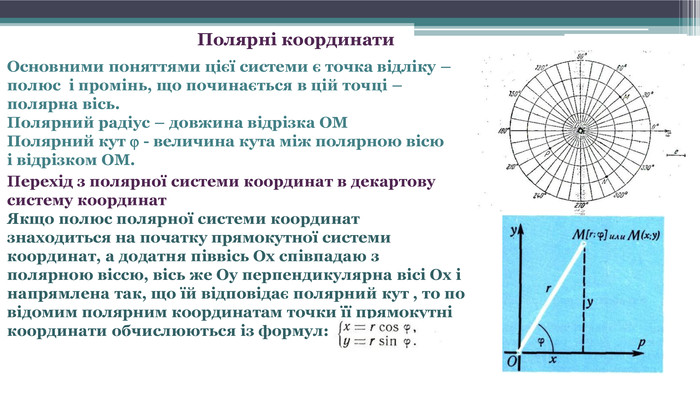
Полярні координати. Перехід з полярної системи координат в декартову систему координат. Якщо полюс полярної системи координат знаходиться на початку прямокутної системи координат, а додатня піввісь Ох співпадаю з полярною віссю, вісь же Оу перпендикулярна вісі Ох і напрямлена так, що їй відповідає полярний кут , то по відомим полярним координатам точки її прямокутні координати обчислюються із формул: Основними поняттями цієї системи є точка відліку – полюс і промінь, що починається в цій точці – полярна вісь. Полярний радіус – довжина відрізка ОМПолярний кут - величина кута між полярною вісю і відрізком ОМ.
Ми з'ясували, що тригонометрія з часом розвинулася в науку про тригонометричні функції. Довели, що тригонометрія тісно пов'язана з фізикою, зустрічається в природі, музиці, астрономії, медицині. Можна наводити нескінченно багато прикладів періодичних процесів живої і неживої природи. Усі періодичні процеси можна описати за допомогою тригонометричних функцій і зображувати на графіках. Використання моделюючої програми " Функції і графіки" дозволило дослідити цікаві математичні криві, що задаються за допомогою тригонометричних рівнянь і побудовати графіки в полярних координатах. Графічне рішення тригонометричних рівнянь і нерівностей привело до розгляду цікавих математичних орнаментів. Тригонометрія знайшла відображення в нашому житті і сфери, в яких вона відіграє важливу роль, розширюватимуться. Висновок
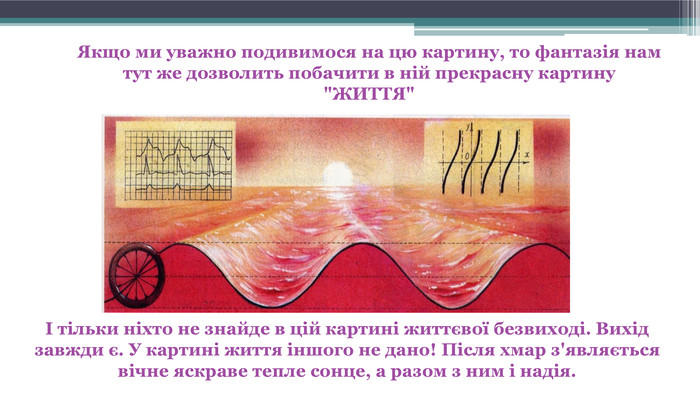
Якщо ми уважно подивимося на цю картину, то фантазія нам тут же дозволить побачити в ній прекрасну картину "ЖИТТЯ"І тільки ніхто не знайде в цій картині життєвої безвиході. Вихід завжди є. У картині життя іншого не дано! Після хмар з'являється вічне яскраве тепле сонце, а разом з ним і надія.
-
 Новомлинська Дар'я Сергіївна 29.10.2022 в 23:44Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Новомлинська Дар'я Сергіївна 29.10.2022 в 23:44Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0 -
 Панасюк Любов Анатоліївна 14.09.2021 в 13:38Дуже гарна презентація. Дякую!Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Панасюк Любов Анатоліївна 14.09.2021 в 13:38Дуже гарна презентація. Дякую!Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0 -
 Челбарах Тетяна Володимирівна 13.08.2021 в 11:33Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0
Челбарах Тетяна Володимирівна 13.08.2021 в 11:33Загальна:5.0Структурованість5.0Оригінальність викладу5.0Відповідність темі5.0


про публікацію авторської розробки
Додати розробку