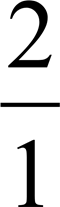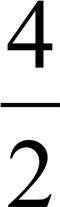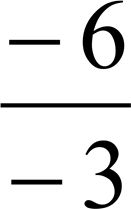Презентація "Вектори в просторі"
Вектори в просторі.
Мета уроку:
1. Математична компетентність: познайомити учнів з вектором, довжиною вектора, рівними, колінеарними векторами, компланарними, співнапрямленими, протилежно напрямленими.
2. Ключові компетентності: спілкування державною мовою – доречно та
коректно вживати в мовленні математичну термінологію;
уміння вчитися впродовж життя – усвідомлювати цінність нових знань і вмінь
 1844 -1850 р.р. - основи векторного числення були закладені дослідженнями англійського математика У.Гамільтона і німецького математика Г. Грассмана по гіперкомплексних числах.
1844 -1850 р.р. - основи векторного числення були закладені дослідженнями англійського математика У.Гамільтона і німецького математика Г. Грассмана по гіперкомплексних числах.
Векторні величини: сила, швидкість, імпульс,…  прискорення….
прискорення….
Вектором називається напрямлений відрізок, з яким можна виконувати математичні дії.
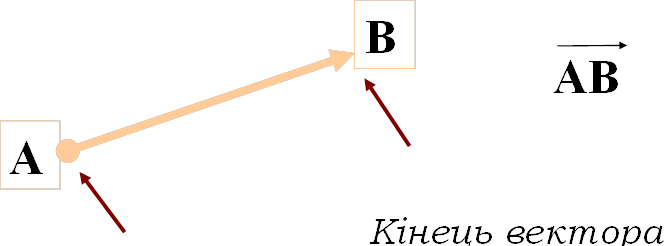
Початок вектора
В
А
 •
•
![]()
АВ, а ![]()
• АА
![]()
АА=0
Назвати вектори зображені на малюнках
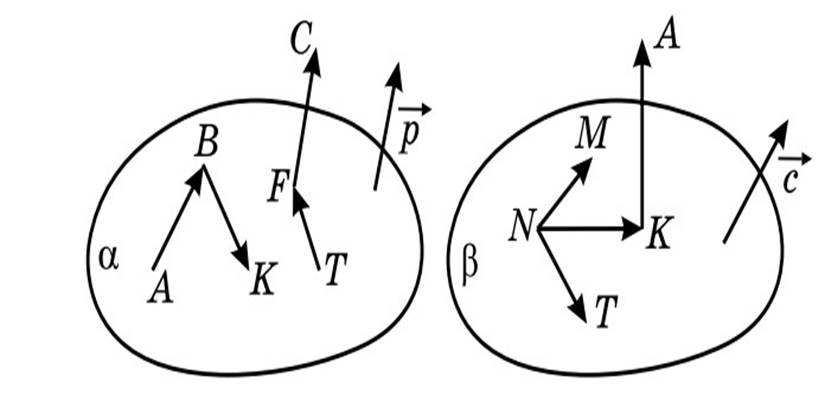
Рис. 1 Рис.2
 |
Координатами вектора а називають координати точки А. Запис а(х;у;z) означає, що вектор а має координати (х;у;z) Координати вектора
 AB(xB −xA; yB −yA;zB −zA)
AB(xB −xA; yB −yA;zB −zA)
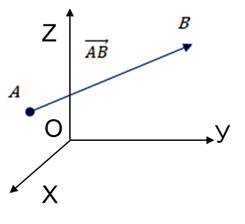
Задача.
Знайдіть координати вектора АВ, якщо А(3;4;2), В(1;-4;5)
![]()
Розв’язання:
![]()
АВ = (1-3;-4-4;5-2) =
![]()
= (-2;-8;3)
Знайдіть координати вектора АВ
![]()
|
A(−3;4;7) |
B(− 3;2;16) |
|
A(−2;5;3) |
B(0;4;−9) |
|
A(0;0;0) |
B(−7;8;12) |
Задача.
Знайдіть координати кінця вектора МК(2;-3;6), якщо
М(3;5;-1)
Розв’язання: х-3 = 2; x = 5; у-5 = -3; у =2;
z-(-1) =6; z = 5.
т.К(5;2;5)
Довжина вектора
![]()
![]() N вектор MN або вектор а
N вектор MN або вектор а
 Довжиною (модулем, абсолютною величиною) вектора називають довжину M відрізка MN.
Довжиною (модулем, абсолютною величиною) вектора називають довжину M відрізка MN.
![]()
![]()
![]()
![]() |MN| = |a| довжина вектора MN вектор КК або нуль- вектор
|MN| = |a| довжина вектора MN вектор КК або нуль- вектор
|
|


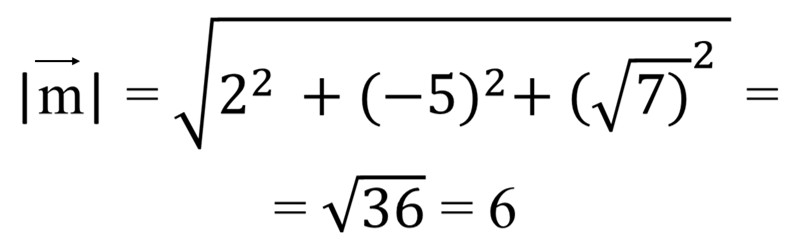
Знайдіть абсолютну величину вектора:
a ![]()

![]() (0;4;−3) a = 02 +42 +(−3)2 =5
(0;4;−3) a = 02 +42 +(−3)2 =5
b ![]()

![]()
![]() (2;−8;3) b = 22 +(−8)2 +32 = 77
(2;−8;3) b = 22 +(−8)2 +32 = 77
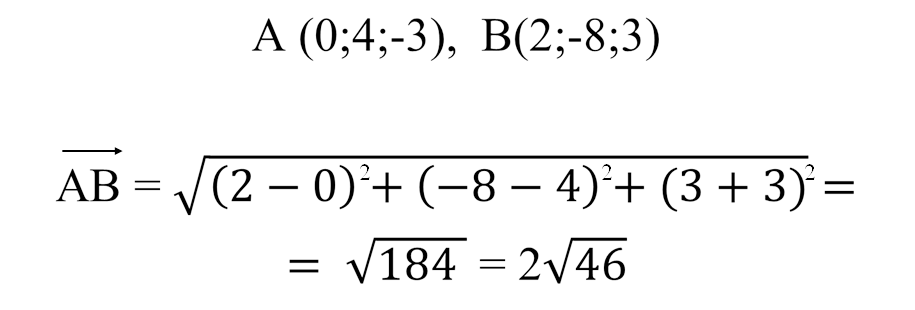 |
Знайдіть абсолютну величину вектора:

Одиничним вектором або ортом називається вектор, довжина якого дорівнює одиниці.
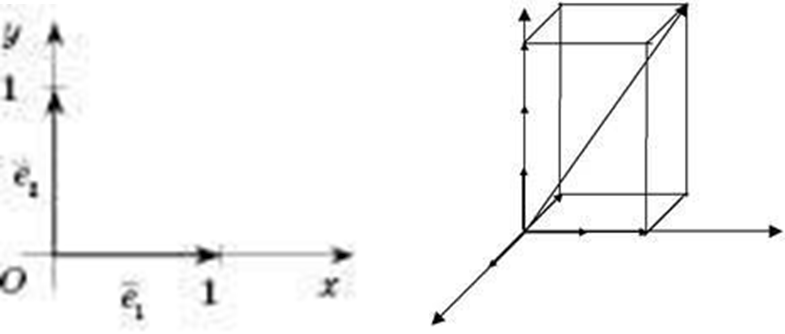


 е₁(1;0;0) е₂(0;1;0) е (0;0;1)3
е₁(1;0;0) е₂(0;1;0) е (0;0;1)3
![]()
![]()
![]() |е₁| = |е₂|= |е 3|= 1
|е₁| = |е₂|= |е 3|= 1
Колінеарні вектори
Колінеарними називають два ненульових вектори, які лежать на одній прямій або на паралельних прямих.
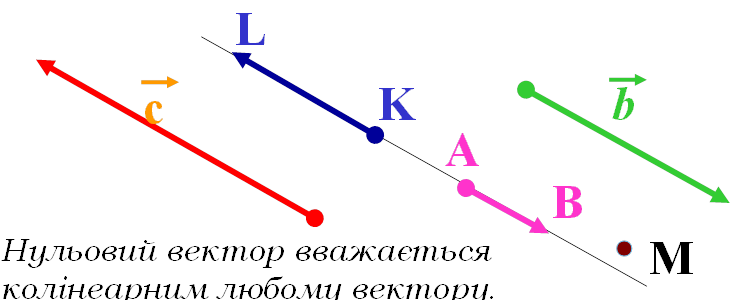
Умова коліанерності векторів
r r
Вектори колінеарні b=a, тому
b1 = b2 =b3
a1 a2 a3
(відповідні координати пропорційні)
Вектори з координатами (2;4;-6) та (1;2;-3) колінеарні, тому що
|
|
= 2 |
Співнапрямлені вектори
![]()
![]()
![]()
![]()
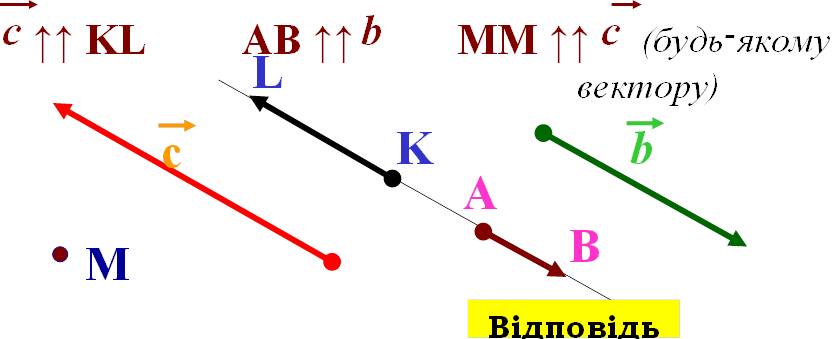 Колінеарні вектори, які мають однаковий напрям, називаються співнапрямленими векторами.
Колінеарні вектори, які мають однаковий напрям, називаються співнапрямленими векторами.
Протилежно направлені вектори
Колінеарні вектори, які мають різні напрями, називаються протилежно прямленими векторами.
![]()
![]()
![]() L b ↑↓ KL AB ↑↓ c
L b ↑↓ KL AB ↑↓ c
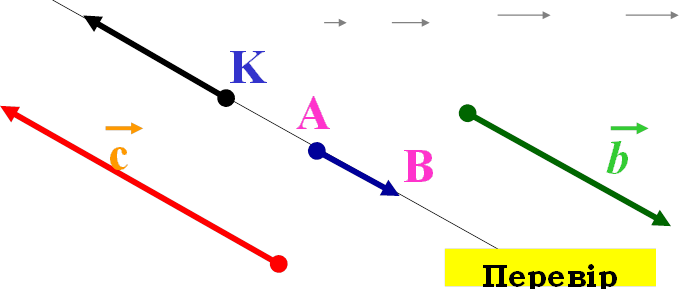 c↑↓ b KL ↑↓ AB
c↑↓ b KL ↑↓ AB

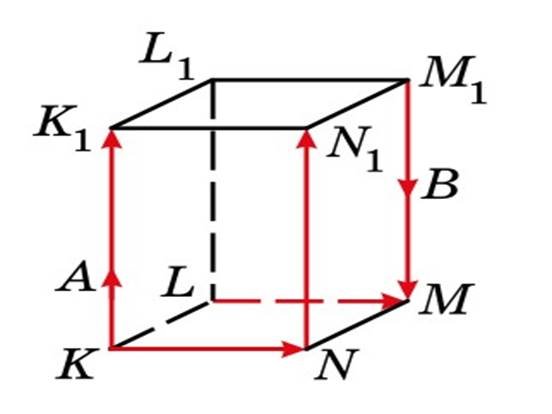 |
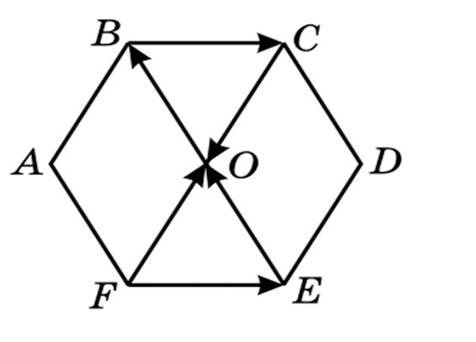
Назвати: рівні вектори; співнапрямлені вектори, колінеарні вектори.
Назвати: рівні вектори; співнапрямлені вектори, колінеарні вектори.
Підсумок уроку
1. Що нового дізнався на уроці?
2. Де використовується це поняття?
3. Що називається вектором?
4. Які бувають вектори?
Домашнє завдання §6п39(опрацювати) №39.3-письмово

До зустрічі!


про публікацію авторської розробки
Додати розробку