Презентація "Властивості функції"
Про матеріал
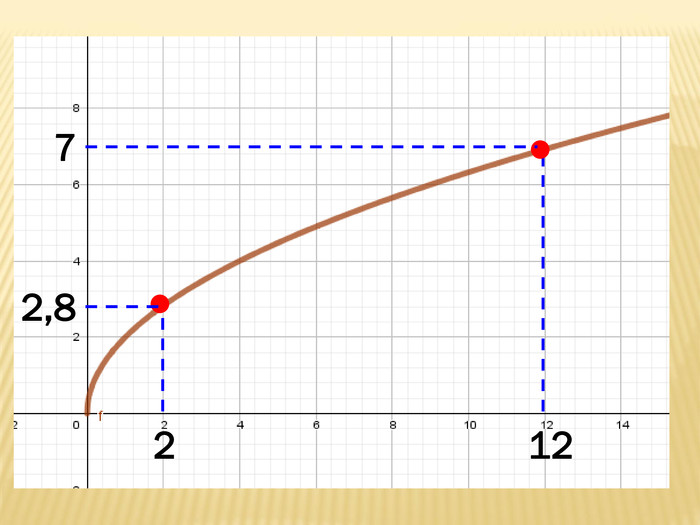
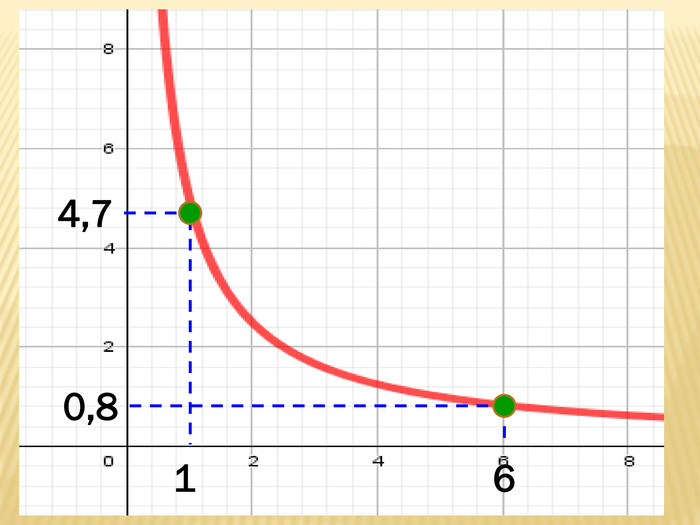
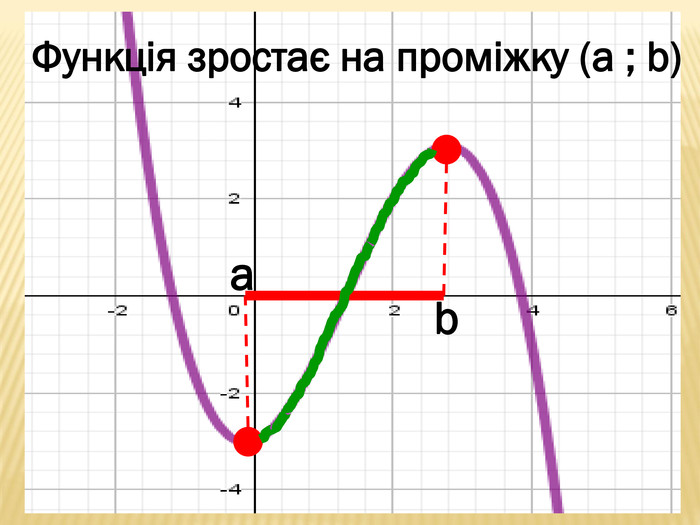
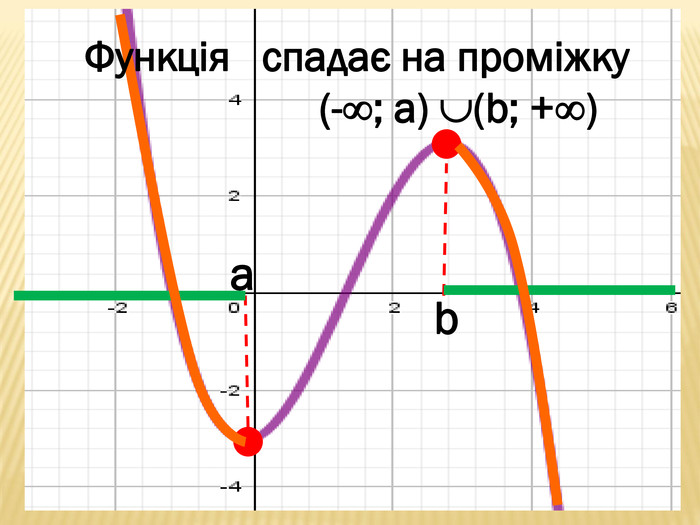
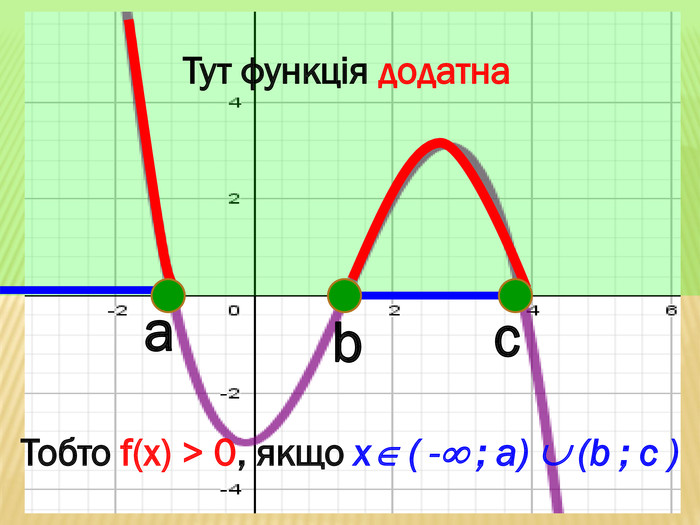
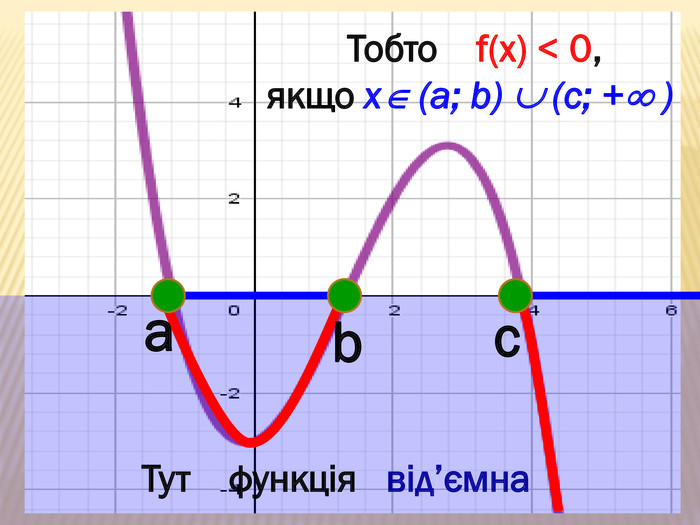
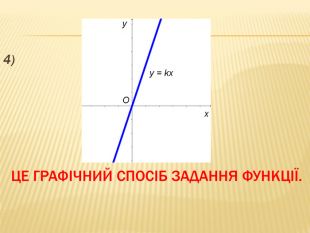
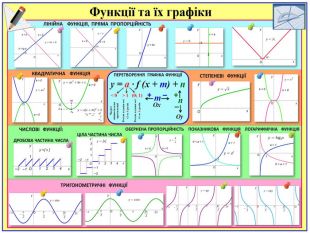
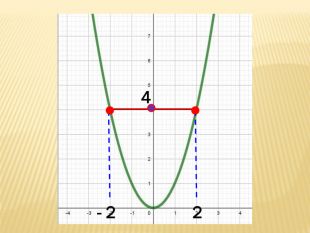
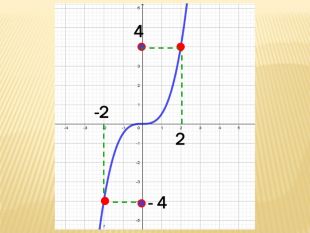
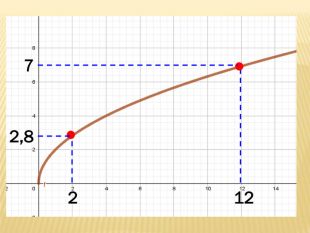
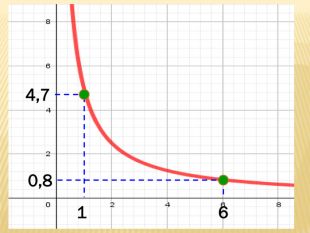
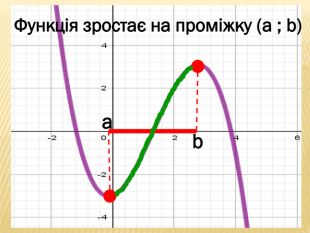
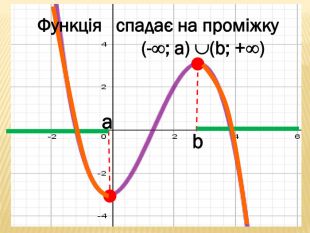
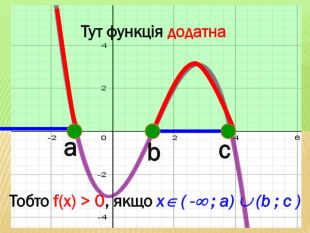
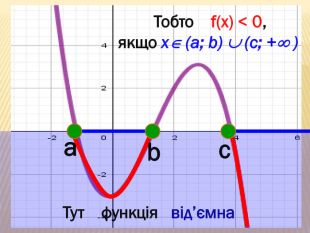
Презентація містить основні поняття з теми "Функція", історичний матеріал, наочно показує властивості функцій, їх графіки. У роботі висвітлено поняття про область визначення, область значень функції, парність, зростання (спадання) функції, знакосталість функції
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Нелін Є.П.)
До уроку
§ 2. Функції Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку





























































-

Баєвська Яніна Георгіївна
11.12.2025 в 06:22
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Євсеєва Людмила Григорівна
05.11.2023 в 10:33
Дякую. Класна презентація
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самойленко Євгеній
12.05.2023 в 09:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Токарєва Олена Олександрівна
09.11.2022 в 14:35
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Мельникова Світлана Олегівна
14.10.2022 в 13:28
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Радчук Тетяна Стратонівна
18.09.2022 в 21:01
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Тимошенко Тетяна Іллівна
11.09.2022 в 21:51
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Докова Валентина Юріївна
09.09.2022 в 13:01
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Кривонос Любов Петрівна
02.09.2022 в 20:46
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Гелешко Наталія
23.08.2022 в 17:55
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Сергієнко Алла Іванівна
03.12.2021 в 11:06
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Красавіна Вікторія Вячеславівна
17.11.2021 в 10:55
дужее дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Івануха Тетяна Володимирівна
15.11.2021 в 17:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Каминіна Ольга
22.09.2021 в 23:02
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 11 відгуків