Урок з використанням інтерактивної дошки.Алгебра і початки аналізу 10 клас профільний рівень. "Обернені тригонометричні функції".

№

Слайд

Зміст

Примітки

1.

Організаційний етап

Вчитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.

Вчитель. Напротязі всього шкільного курсу математики ми розглянули прямі та обернені дії над числами. Наприклад, дія, обернена додаванню – віднімання, множенню – ділення, піднесенню до степеня – добування кореня. На минулому уроці ми з’ясували, що дія, обернена до знаходження тригонометричних функцій – знаходження так званих аркфункцій.

Слайд має інформаційно- ілюстративний характер. Перехід до наступного слайду:

2.

Мотивація навчальної діяльності

Вчитель пропонує учням поринути у історію позначень обернених тригонометричних функцій (ОТФ).

Вчитель.

Позначати обернені тригонометричні функції за допомогою приставки arc (від лат. arcus, дуга) вперше почав австрійський математик Карл Шерфер (1716-1783).

Англійська та німецька математичні школи до кінця ХІХ століття пропонували інші позначення: sin-1, 1\(sin) але вони не закріпились.

Слайд має інформаційно- ілюстративний характер. Перехід до наступного слайду:

3.

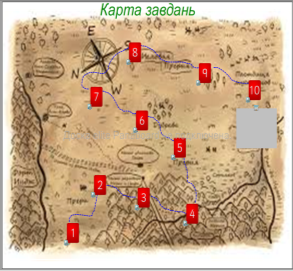
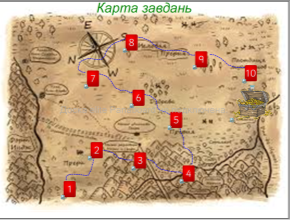
Формулювання мети та завдань уроку

Вчитель. На сьогоднішньому уроці ми удосконалимо знання означень та властивостей ОТФ. Перед вами карта завдань. Виконавши всі запропоновані завдання, ми дізнаємось ім’я французького математика, завдяки якому закріпилося позначення ОТФ таким, яким ми користуємось сьогодні.

Перехід до завдання відбувається за гіперпосиланням до відповідного номера

( - ).

Перехід до останнього слайду здійснюється, відкривши затемнену частину екрану

↓

4.

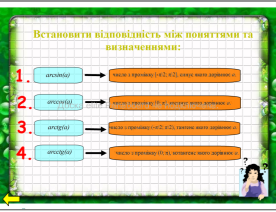
Актуалізація опорних знань учнів

Відповідно до мети уроку перед розв'язуванням письмових вправ слід активізувати такі знання і вміння учнів:

• відтворювати означення:

arcsin(a), arccos(a), arctg(a), arcctg(a);

• обчислювати значення основних аркфункцій;
• розпізнавати відповідні до тригонометричних обернені функції;
• визначати властивості ОТФ (область визначення, множина значень, парність/непарність, нулі функцій);
• розпізнавати графіки відповідних аркфункцій.

Для виконання завдання використовується перо.

Вказівка:

(Перетягування)

Перевірка:

Повернення до карти завдань:

(Гіперпосилання)

5.

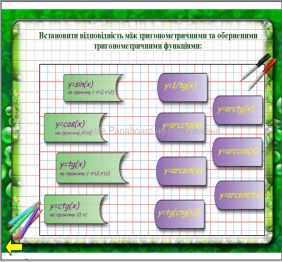
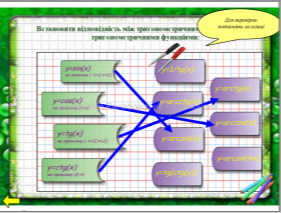
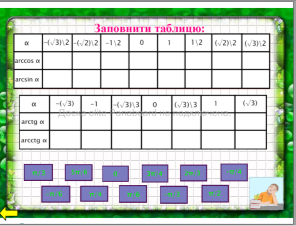
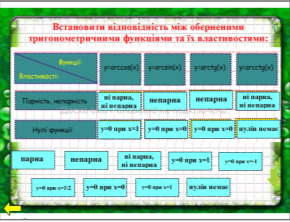
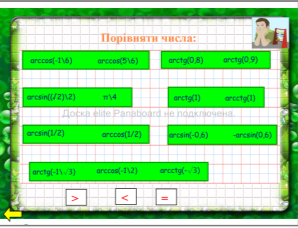
Для виконання завдання використовується перетягування.

Перевірка здійснюється наступним чином: неправильні відповіді завдяки заздалегідь встановленому порядку, розташовуються на задньому плані, правильні, відповідно – на передньому.

Повернення до карти завдань:

(Гіперпосилання)

6.

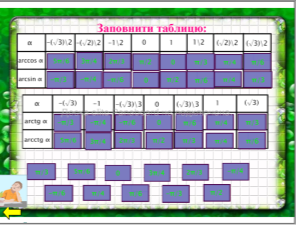
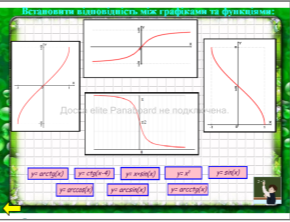
Для виконання завдання використовують множинне клонування.

Перевірка:

(Перетягування)

Повернення до карти завдань:

(Гіперпосилання)

7.

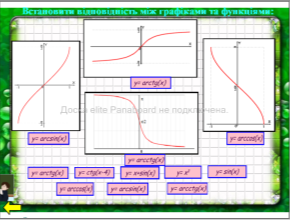
Для виконання завдання використовують множинне клонування.

Перевірка:

(Перетягування)

Повернення до карти завдань:

(Гіперпосилання)

8.

Для виконання завдання використовують множинне клонування.

Перевірка:

(Перетягування)

Повернення до карти завдань:

(Гіперпосилання)

9.

Для виконання завдання використовують перетягування.

Перевірка:

(Перетягування)

Повернення до карти завдань:

(Гіперпосилання)

10.

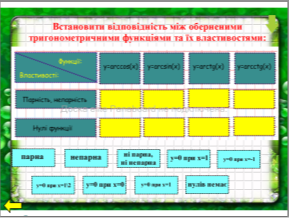
Удосконалення вмінь

Учні продовжують роботу над засвоєнням властивостей обернених тригонометричних функцій.

Для виконання завдання використовують множинне клонування.

Вказівка:

(Перетягування)

Перевірка:

Повернення до карти завдань:

(Гіперпосилання)

11.

Для виконання завдання використовують множинне клонування (альтернативний варіант – використання пера).

Перевірка:

(Перетягування)

Повернення до карти завдань:

(Гіперпосилання)

12.

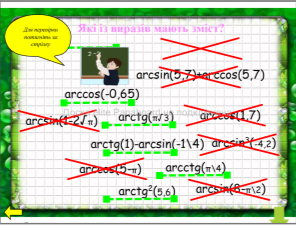
Для виконання завдання використовується перетягування.

Вказівка:

(Перетягування)

Перевірка:

та

Повернення до карти завдань:

(Гіперпосилання)

13.

Для виконання завдання використовують множинне клонування (альтернативний варіант – використання пера).

Перевірка:

(Перетягування)

Повернення до карти завдань:

(Гіперпосилання)

14.

Підсумок уроку

Вчитель. Ось і закінчилась наша подорож по історичним сторінкам минулого обернених тригонометричних функцій. Саме завдяки Жозефу-Луї Лагранжу, ми користуємось позначенням ОТФ з приставкою arc.

Слайд має інформаційно- ілюстративний характер. Перехід до наступного слайду:

15.

Рефлексія

Вчитель пропонує учням обрати той малюнок із зображенням емоції (веселий, байдужий, сумний), який найбільше відповідає їхньому настрою.

Для виконання завдання використовують множинне клонування.

Перехід до наступного слайду:

Музичний супровід:

16.

Домашнє завдання

Різнорівневе домашнє завдання: для дітей із різним рівнем навчальних досягнень