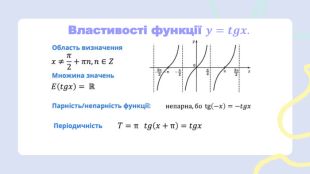
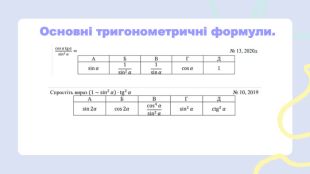
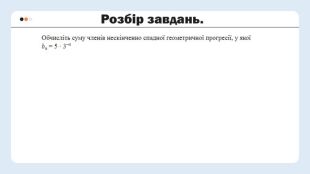
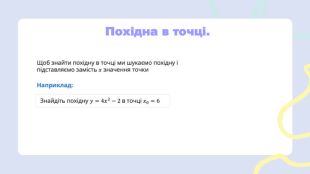
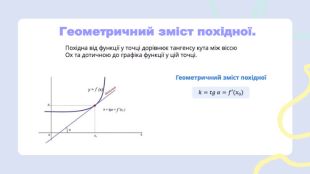
Презентація з алгебри по темі: "Вся алгебра до НМТ".
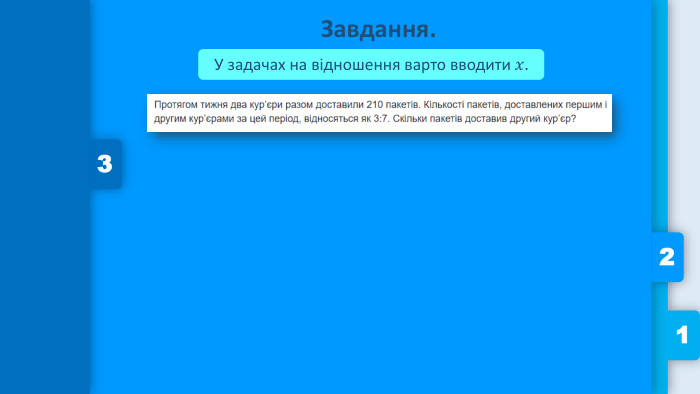
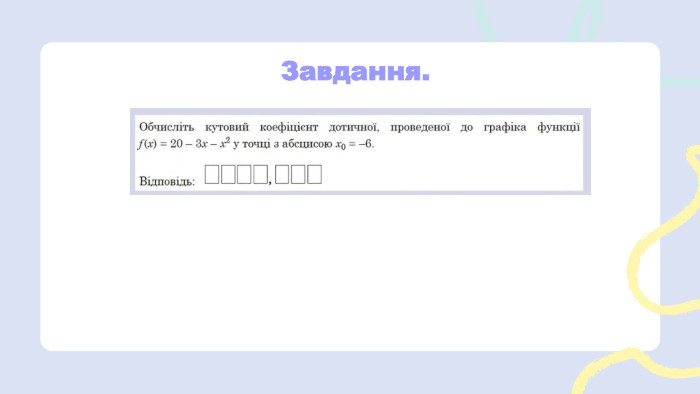
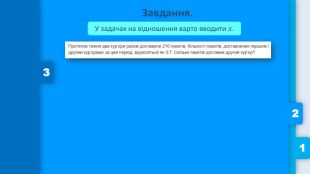
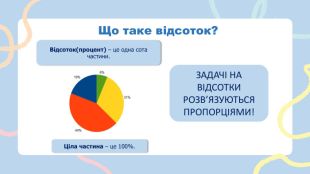
УСЯ АЛГЕБРАДО НМТ. RYSETSKIY MAXIM123
УСЯ АЛГЕБРАДО НМТ. RYSETSKIY MAXIM1 Що таке відношення?Відношення показує скільки частинок щось становить від іншого.1:2 23
УСЯ АЛГЕБРАДО НМТ. RYSETSKIY MAXIM1 Що таке відношення?Відношення показує скільки частинок щось становить від іншого.1:2 2 Завдання. У задачах на відношення варто вводити 𝑥. 3
УСЯ АЛГЕБРАДО НМТ. RYSETSKIY MAXIM1 Що таке відношення?Відношення показує скільки частинок щось становить від іншого.1:2 2 Завдання. У задачах на відношення варто вводити 𝑥. 3 Що таке пропорція?Пропорція – це рівність двох відношень.3 :4=6 :81 :2=4 :851=255 Основна властивість пропорції. Добуток крайніх членів дорівнює добутку середніх.51=255→1∙25=5∙5 𝑥2=84→ 3𝑥=124→
Що таке відсоток?Відсоток(процент) – це одна сота частини. Ціла частина – це 100%. ЗАДАЧІ НА ВІДСОТКИРОЗВ’ЯЗУЮТЬСЯ ПРОПОРЦІЯМИ!
Завдання.
Завдання.
Завдання.
Степені. Степінь з від’ємним показником.𝑎−𝑛=1𝑎𝑛, 𝑎≠0 (2)−3=(−5)−2=
Степені. Множення степеней з однаковими основами.𝑎𝑚∙𝑎𝑛=𝑎𝑚+𝑛 62∙6=43∙42=
Степені. Ділення степеней з однаковими основами.𝑎𝑚:𝑎𝑛=𝑎𝑚𝑎𝑛=𝑎𝑚−𝑛 512:59=2829=
Степені. Число підноситься до декілька степеней.(𝑎𝑚)𝑛=𝑎𝑚∙𝑛 (23)2=(4𝑥𝑎2𝑦3)2=
Що таке функція?Функція – це залежність однієї величини від іншої.𝑦=4𝑥+3 𝑓(𝑥)=4𝑥+3 𝑥 −незалежна змінна, аргумент𝑦 −залежна змінна, функція функції
Нулі функції – таке значення 𝑥 при якому 𝑦=0.𝑦=4𝑥−8? На графіку нуль функції – це точка перетину графіку з віссю абсцис.𝒙𝟏 𝒙𝟐 𝒙𝟏,𝒙𝟐−нулі функції.
Завдання.
Завдання.
ПАРНА ФУНКЦІЯ
ПАРНА ФУНКЦІЯ
ПАРНА ФУНКЦІЯ
НЕПАРНА ФУНКЦІЯ
НЕПАРНА ФУНКЦІЯ
Область визначення.
Область значення.
Область визначення – це всі значення змінної х при яких функція має зміст. Позначення D(f)Вид функціїОбласть визначенняу = f(х), де f(х) многочлен. R або (-∞; ∞)g(x)≠0f(x)≥0g(x)˃0 Область значень – це всі значення змінної у. Позначення Е (f)
Завдання.
Завдання.
Лінійна функція.
Завдання.
Лінійне рівняння. Лінійне рівняння - це рівняння виду𝑎∙𝑥=𝑏 де 𝑎 і 𝑏 −деякі числа, 𝑥−невідоме 2𝑥=10 12𝑥=8 12𝑥+4=8
Завдання.
Завдання.
Квадратне рівняння.
Дискримінант.
Дискримінант. Знаки дискримінант. Якщо 𝐷<0, то квадратне рівняння не має розв′язку. Якщо 𝐷=0, то квадратне рівняння має один корінь. Якщо 𝐷>0, то квадратне рівняння має два різних коренів.
Теорема Вієта.
Завдання.
Завдання.
Завдання.3𝑥2+5𝑥+2=0
Квадратична функція.
Квадратична функція.
Нулі функції.
Проміжки. Дужки𝑥<𝑎 𝑥>𝑎 −∞ +∞ 𝑎 𝑥<𝑎 𝑥>𝑎 𝑥≥𝑎 𝑥≤𝑎 якщо знак строгийякщо знак нестрогийзафарбована точкавиколота точкадужка кругла «(« - точка не включаєтьсядужка квадратна «[« - точка включається
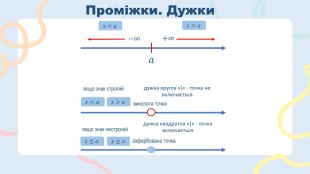
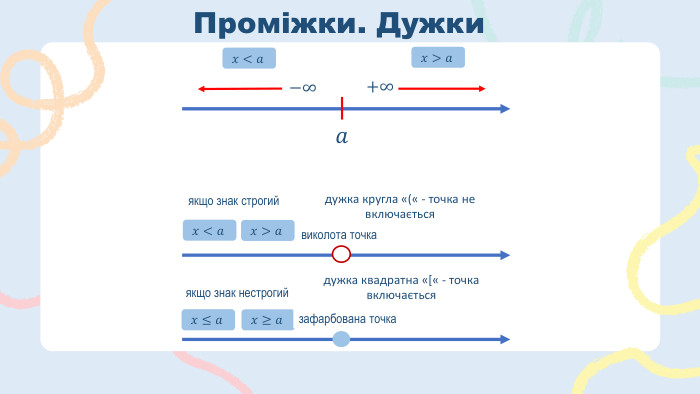
Властивості нерівностей.1. Можна переносити з одного боку нерівності в інший, але змінювати знак на протилежній.2. Можна розкривати дужки і зводити подібні доданки.3. Можна множити і ділити обидві частини нерівності на одне й теж саме число, крім 0!4. При діленні чи множені нерівності на від’ємне число, знак нерівності треба розвернути!!!!5𝑥+4<19
Лінійна нерівність. Лінійна нерівність – це нерівність виду:𝑎𝑥<𝑏,де 𝑎 і 𝑏 −деякі числа, 𝑥 −змінна Окремі випадки:0𝑥>𝑎, 𝑎−від′ємне 𝑥∈𝑅0𝑥<𝑎,𝑎−від′ємне 𝑥∈∅ Запам’ятай!Від’ємний коефіцієнт перед x змінює знак нерівності:−𝑥>4𝑥<−4
Лінійна нерівність. Приклад:6𝑥+2−2𝑥≥06𝑥+12−2𝑥≥06𝑥−2𝑥≥−124𝑥≥−12𝑥≥−3 −3 𝑥∈[−3;+∞)
Лінійна нерівність
Завдання 1.
Квадратична нерівність. Квадратична нерівність – це нерівність виду:𝑎𝑥2+𝑏𝑥+𝑐≥0,де 𝑎 і 𝑏 −деякі числа, 𝑥 −змінна Є два методи розв’язку квадратичних нерівностей: Метод параболи;Метод інтервалів.
Метод параболи. Для цього методу потрібно базово розуміти, що таке квадратична функція. Квадратична функція має вигляд:𝑦=𝑎𝑥2+𝑏𝑥+𝑐параболаде 𝑎напрямок віток𝑐перетин з віссю 𝑂𝑦вершина параболи:𝑥в=−𝑏2𝑎, 𝑦в=𝑦(𝑥в)
Метод параболи
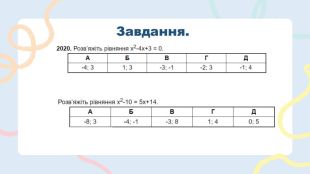
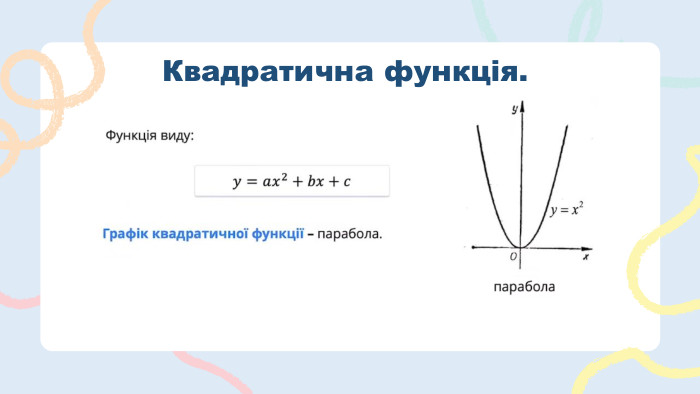
Метод параболи. Кроки розв’язання квадратичної нерівності: Знаходимо нулі функції, прирівнюючи квадратичну функцію до нуля, використовуючи дискримінант. Враховуючи кількість коренів і знак коефіцієнта 𝑎, креслиться графік параболи. Обираються порожні або зафарбовані точки, в залежності від вигляду знака нерівності. Зафарбовується правильний інтервал. Записуємо відповідь. Лайфхак!Якщо хочеш, щоб гілки параболи завжди були спрямовані вгору, у випадках, коли 𝑎<0, треба спочатку обидві частини нерівності помножити на (−1). Не забудь, що на протилежний поміняється знак нерівності.
Метод параболи
Метод параболи2𝑥2−7𝑥−4≤0
Метод інтервалів. Кроки розв’язання квадратичної нерівності: Нулі функції.2. На числовій прямій позначаємо ці точки та знаходимо знак кожного проміжку.3. Залежно від умови завдання обираємо правильні проміжки.
Приклади. Розв’яжіть нерівність: 𝑥−35−𝑥>0
Приклади. Розв’яжіть нерівність: 𝑥2+7𝑥−30≥0
Модуль.
Модуль.
Рівняння з модулем.
Рівняння з модулем.
Корінь.
Корінь.
Корінь.
Винесення/внесення числа.
Ірраціональність в знаменнику.
Ірраціональні рівняння. Якщо під коренем міститься невідоме – це ірраціональне рівняння.𝑥+3=73𝑥+𝑥=103𝑥+5−3𝑥−5=10 ОДЗ квадратного кореня. Число, яке стоїть під квадратним коренем має бути більше за 0.2. Значенням квадратного кореня має бути більше за 0.𝑥=𝑎𝑥≥0,𝑎≥0
Ірраціональні рівняння. Рівняння типу:𝑥=𝑎Поширений прийом розв’язання ірраціональних рівнянь – зведення у квадрат.
Ірраціональні рівняння.
Ірраціональні рівняння.
Ірраціональні нерівностіНерівність називають ірраціональною, якщо вона містить змінну під знаком кореня. Розв’язання: В загальному, розв’язок ірраціональних нерівностей такий ж як для ірраціональних рівнянь𝑛𝑥≥𝑎(𝑛𝑥)𝑛≥𝑎𝑛→𝑥≥𝑎𝑛
Ірраціональні нерівностіОДЗ: Для коренів парного степеня – підкореневий вираз ≥𝟎. Для коренів непарного степеня обмежень немає - 𝒙∈𝑹. Окремі випадки!3𝑥−9≤4𝑥+2 Для нерівностей такого типу потрібне подвійне ОДЗ:3𝑥−9≥04𝑥+2≥0𝑥∈[3;+∞) ЗАПАМ’ЯТАЙ!𝒙>−𝟐𝒙∈𝑹𝒙<−𝟐𝒙∈∅
Ірраціональні нерівності
Приклад. Розв′яжіть нерівність:𝑥2−5𝑥+4≤2
Показникова функція.
Властивості.
Завдання.
Показникові рівняння.
Завдання.
Завдання.
Завдання.
Завдання.
Завдання.
Завдання.
Завдання.
Завдання.
Показникові нерівностіПоказниковими вважаються нерівності, які включають в себе показникову функцію.𝑎𝑓(𝑥)>𝑎𝑔(𝑥) 𝑎𝑓(𝑥)<𝑎𝑔(𝑥)𝑎𝑥>𝑎𝑦→𝑥>𝑦 при 𝑎>1𝑎𝑥>𝑎𝑦→𝑥<𝑦 при 0<𝑎<1 2𝑥<322𝑥<25𝑥<5
Завдання
Завдання
Логарифмічні рівняння.
Логарифмічні рівняння.
Логарифмічні рівняння.
Логарифмічні рівняння.
Логарифмічні нерівність
Логарифмічні нерівність
Логарифмічні нерівність
Завдання
Логарифмічні нерівність
Логарифмічні нерівність
Завдання
Завдання
Системи рівнянь(підстановка.)
Системи рівнянь(додавання.)
Системи рівнянь(графічний.)
Системи рівнянь(заміна.)
Системи нерівностей
Системи нерівностей
Завдання
Завдання
Властивості функції 𝒚=𝒔𝒊𝒏𝒙.
Властивості функції 𝒚=𝒄𝒐𝒔𝒙. Лише косінус парний, всі інші тригонометричні функції непарні!
Властивості функції 𝒚=𝒕𝒈𝒙.
Завдання.
Основні тригонометричні формули.
Основні тригонометричні формули.
Основні тригонометричні формули.
Що таке прогресії?Прогресія- послідовність величин, кожна з яких залежна від попередньої. Ця залежність спільна для всієї прогресіїї Приклади прогресійарифметична прогресія(+)геометрична прогресія(*)
Що ж таке арифметична прогресія?Арифметична прогресія- це числова послідовність, де до кожного наступного члена додається число d.
Розбір завдань.
Формула n-го члена арифметичної прогресіїФормула n-го члена арифметичної прогресії
Розбір завдань.
Розбір завдань.
Формула суми арифметичної прогресіїСума перших n членів арифметичної прогресії
Розбір завдань.
Розбір завдань.
Що ж таке геометрична прогресія?Геометрична прогресія- це числова послідовність, де до кожного наступного члена множиться на число q.
Розбір завдань.
Формула n-го члена геометричної прогресіїФормула n-го члена геометричної прогресії
Розбір завдань.
Розбір завдань.
Формула перших n членів геометричної прогресіїСума перших n членів геометричної прогресії
Розбір завдань.
Нескінченно спадна геометричної прогресії
Сума всієї нескінченно спадної геометричної прогресії
Розбір завдань.
Розбір завдань.
Додаткова інформація.
Похідна.
Похідна суми чи різниці.
Похідна в точці.
Геометричний зміст похідної.
Завдання.
Механічний зміст похідної.
Завдання.
опції драйв(вперед) і реверс(назад)
НАПРИКЛАД
НАПРИКЛАД
ПОХІДНА-ІНТЕГРАЛ: ОПЦІЇ ДРАЙВ-РЕВЕРС
Первісна. Інтеграл𝑓𝑥𝑑𝑥=𝐹𝑥+𝐶−Невизначений інтеграл.𝑎𝑏𝑓𝑥𝑑𝑥 −Визначений інтеграл.
Первісна. Інтеграл
Первісна. Інтеграл
Первісна. Інтеграл
Первісна. Інтеграл
Визначений інтеграл(Площа).
Визначений інтеграл(Площа).
Визначений інтеграл(Площа).
Визначений інтеграл(Площа).
Визначений інтеграл(Площа).
Перестановки. Вчитель фізкультури захотів ваш клас построїть в шеренгу. Кількість перестановок – факторіал кількості предметів.
Факторіал.
Завдання.
Розміщення.
Розміщення.
Завдання.
Комбінації.
Комбінації.
Завдання.
КІНЕЦЬ!ДЗ В TELEGRAM!
про публікацію авторської розробки
Додати розробку