Розв’язування симетричних систем рівнянь вищих степенів із двома невідомими

 Розв’язування симетричних систем рівнянь вищих степенів із двома невідомими

 У цій статті я хочу розглянути один цікавий спосіб розв’язування симетричних систем рівнянь вищих степенів із двома невідомими у полі дійсних чисел. Такі системи  часто були і є невід’ємним атрибутом математичних олімпіад.

 Розглянемо систему рівнянь:

, де

Така система є симетричною: невідомі та є рівноправними і можуть бути замінені одна одною, при цьому система не зміниться. При цьому, якщо існує деякий розв’язок системи розв’язком системи буде також пара

Для розв’язування такої системи введемо наступні позначення;

Отже, , ,   і т. д.

Крім того для легко вивести наступне рекурентне співвідношення:

Розглянемо конкретний приклад.

Розв’язати систему рівнянь:

Отже:

Тепер спробуємо виразити через

Звідси:

Скоротимо на 6 і отримаємо звичайне квадратне рівняння:

Оскільки , отримуємо сукупність двох систем:

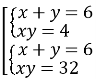
Перша система є теоремою Вієта для квадратного рівняння виду .

Звідси:

Друга система є теоремою Вієта для квадратного рівняння виду .

, тому друга система розв’язку немає.

Отже, розв’язки вихідної системи

Як бачимо, даний метод привів нас від системи 5 степеня, до квадратного рівняння відносно

Думаю, що доцільно ознайомити із даним методом тих учнів, які цікавляться математикою на поглибленому рівні.