Урок "Правильні многокутники"

Урок №1.

Тема уроку. Правильні многокутники

Мета уроку: формування поняття правильного многокутника, центра і центрального кута правильного многокутника. Формування вмінь застосовувати вивчений матеріал до розв’язування задач.

Тип уроку: комбінований.

Наочність і обладнання: моделі многокутників, підручник, презентація PowerPoint

Хід уроку

І. Організаційний момент.

ІІ. Повторення й узагальнення знань про многокутники.

Приклади многокутників у природі. (мал. 1.) (слайди  3-4)

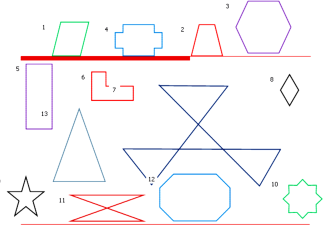Бесіда з учнями: (Мал. 2, 3, 4)

1. Сформулюйте означення многокутника, його вершини, сторін, діагоналей.
2. Які многокутники вам відомі?     Приклади многокутників (слайд 5)
3. Що таке кут многокутника?
4. Який многокутник називається опуклим (неопуклим) (слайд 6).
5. Чи можна побудувати чотирикутник з двома прямими і двома тупими кутами? Відповідь поясніть.
6. Напівправильні многокутники (слайд 7).

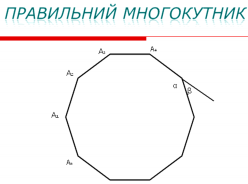
 ІІІ. Сприйняття і усвідомлення нового матеріалу

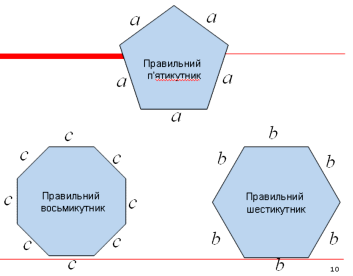
   Серед різномаїття опуклих многокутників виділяють такі многокутники, у яких усі сторони й усі кути рівні. Такі многокутники називаються правильними  (мал.5)                                             (слайд 8)

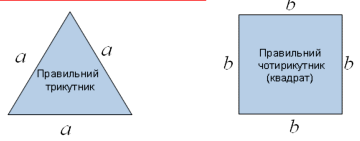
Запитання до класу:  (мал. 6)           (слайди 9-10)

1. Який трикутник є правильним7
2. Який чотирикутник є правильним?
3. Знайдіть кути правильного восьмикутника.
4. Скільки сторін має правильний многокутник, якщо кут при його вершині дорівнює 120⁰?

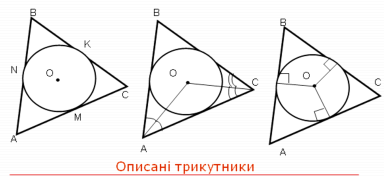IV. Повторення відомостей про вписані й описані трикутники

Бесіда.   

Запитання до класу з використанням таблиці (мал. 7) . (слайди 12 – 13)

1. Яке коло називається описаним навколо трикутника?
2. Чи можна описати коло навколо будь-якого трикутника?
3. Де міститься центр кола, описаного навколо трикутника?
4. Яке коло називається вписаним у трикутник?
5. Чи можна вписати  коло в будь-який трикутник?
6. Де міститься центр кола, вписаного в трикутник?

V. Сприйняття і усвідомлення нового матеріалу

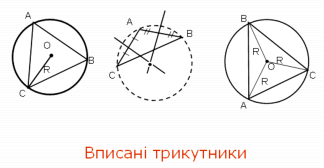
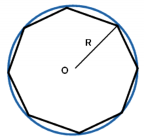
   Навколо будь-якого правильного многокутника можна  описати коло  і  до того  ж  тільки одне.

Многокутник називається вписаним у коло, якщо всі його вершини лежать на колі (мал.. 8).        (слайд 15)

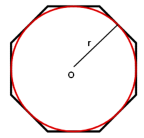
     В будь-який правильний многокутник можна вписати коло  і  до того ж  тільки одне.

Многокутник називається описаним навколо кола, якщо всі його сторони дотикаються до цього кола (мал.. 9).   (слайд 16)

Теорема.    Правильний многокутник є вписаним у коло й описаним навколо кола. 

                                                                                                                                                      (слайд  17)      

(Пропоную теорему довести разом з учнями. Вчитель біля дошки, а учні допомагають з місця)

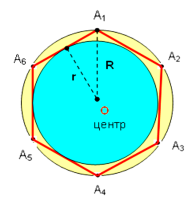
Для правильного многокутника центри вписаного і описаного кіл співпадають (мал.. 10). (слайд 18)

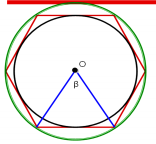
Означення центрального кута.

Кут під яким видно сторону правильного многокутника з його центра,  називається центральним кутом многокутника. (Мал. 11. Слайд 19)

Запитання до класу

1. Чому дорівнює центральний кут правильного трикутника?
2. Чому дорівнює центральний кут правильного чотирикутника?
3.  Чому дорівнює центральний кут правильного n-кутника?

6.  Закріплення й осмислення нового матеріалу.

Розв’язування прав

Вправа 1. (Слайд 20)

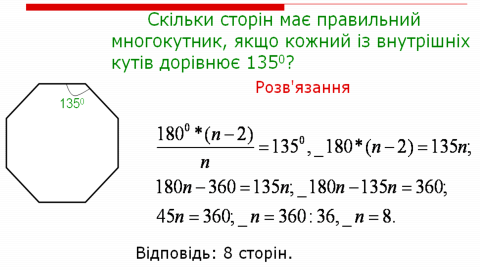
Вправа 2. (Слайд 21)

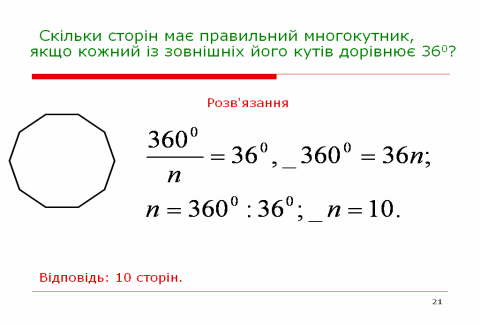
7. Домашнє завдання

Опрацювати §11.

Завдання 12

9(б), 10(в).

Задача.

    Дано правильний шестикутник. Доведіть, що радіус описаного кола в двічі більший радіуса вписаного кола.

8. Підсумок уроку

1. Який многокутник називається правильним?
2. Який многокутник називається вписаним у коло? (описаним навколо кола?)
3. Чи завжди можна вписати коло в правильний многокутник? (описати коло навколо правильного многокутника?)
4. Що таке центр правильного многокутника? (апофема?)
5. Що таке центральний кут правильного многокутника? Чому він дорівнює?