Презентація з геометрії для 11 класу "Поняття многогранника. Формула Ейлера"
Про матеріал
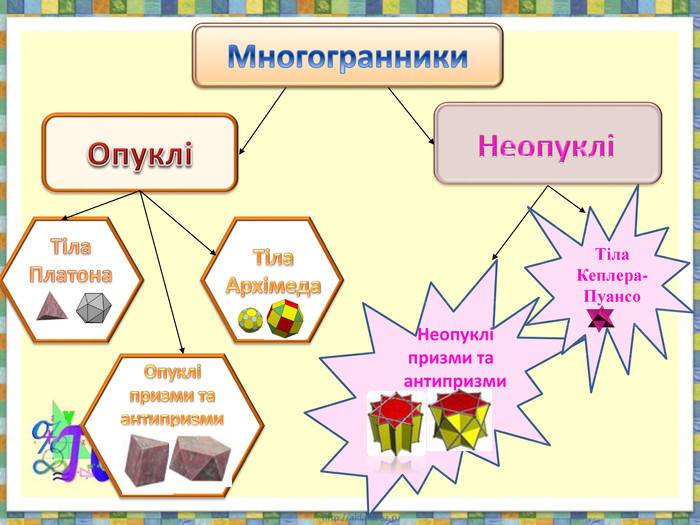
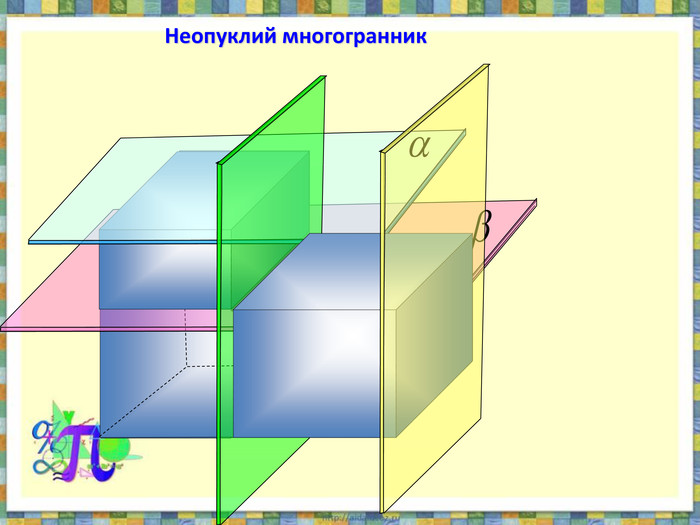
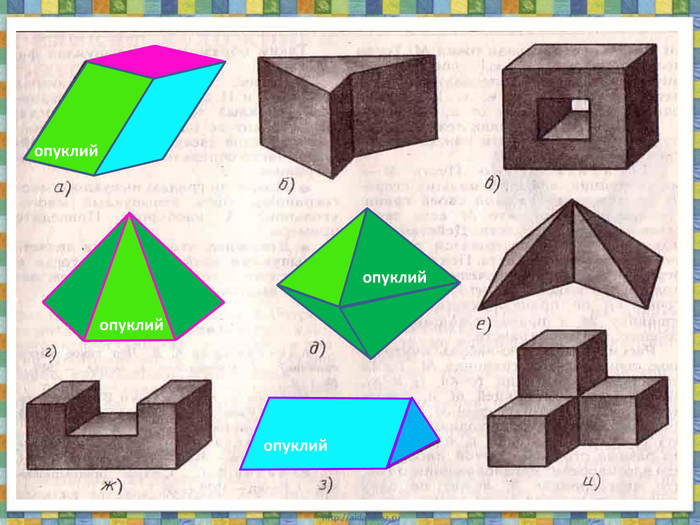
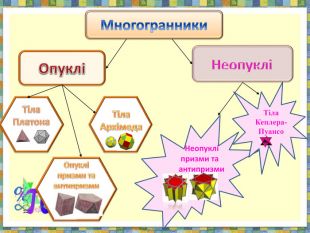
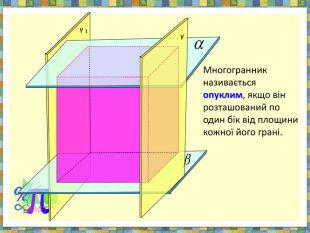
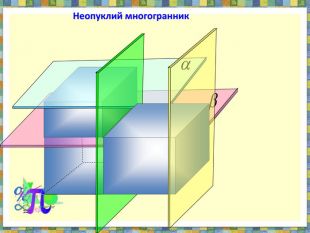
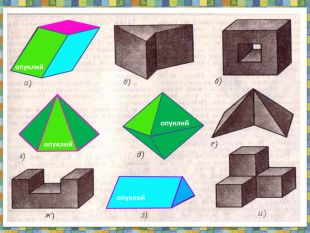
Проезентація "Поняття многогранника. Формула Ейлера" містить означення опуклого та неопуклого многогранника,
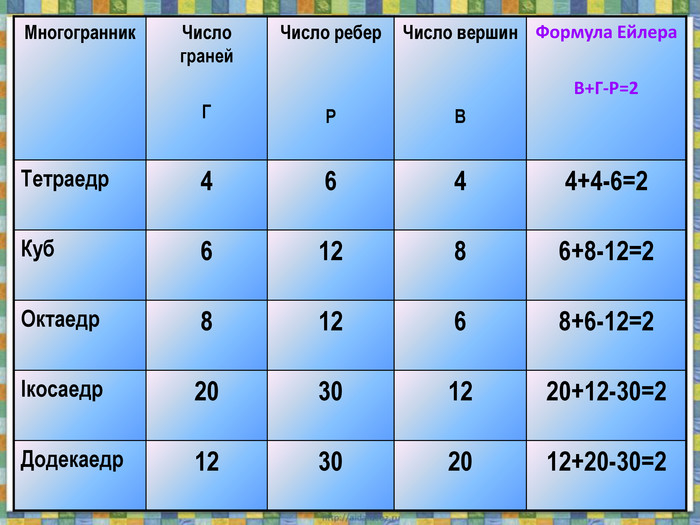
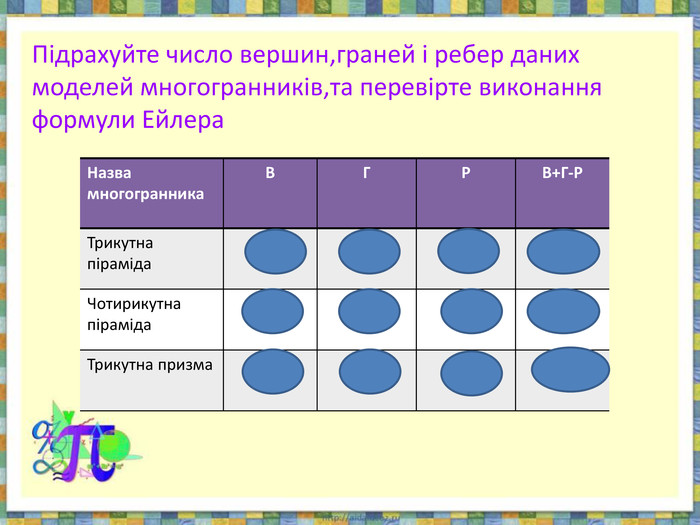
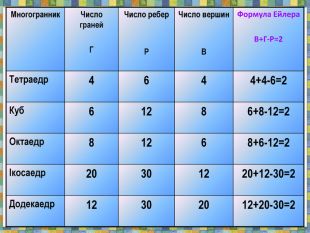
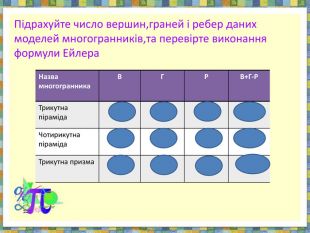
теорему Ейлера для опуклих многогранників.Всі означення проілюстровані анімованими малюнками. Також є практичні завдання.
многогранникиПерегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Чудова презентація!
-
Використаю при поясненні теми.Дуже гарні анімації!
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку