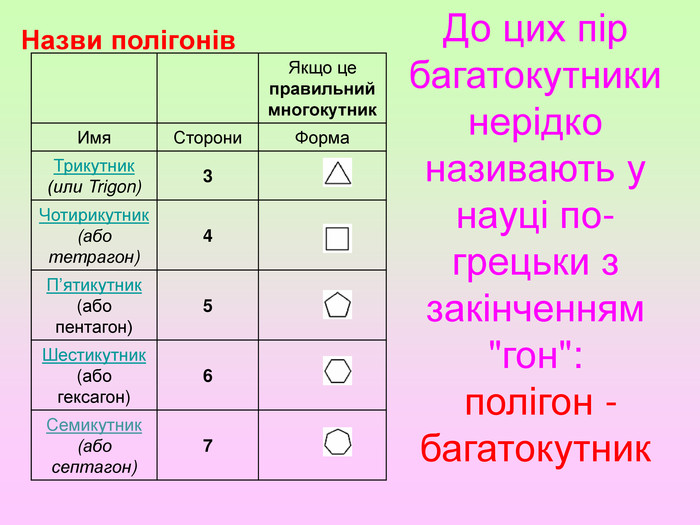
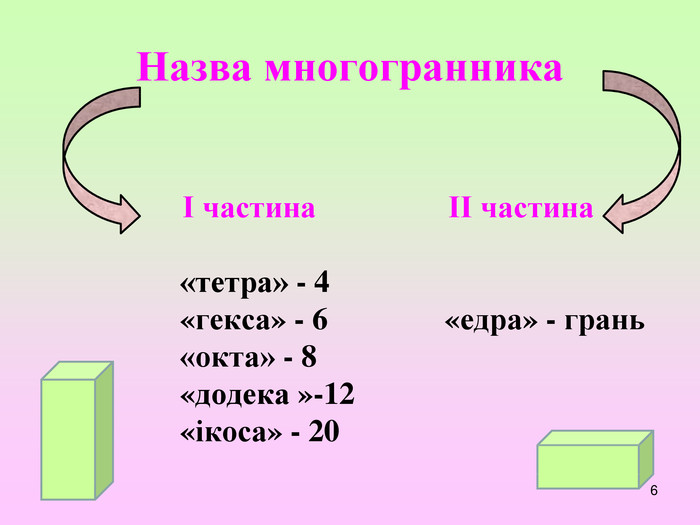
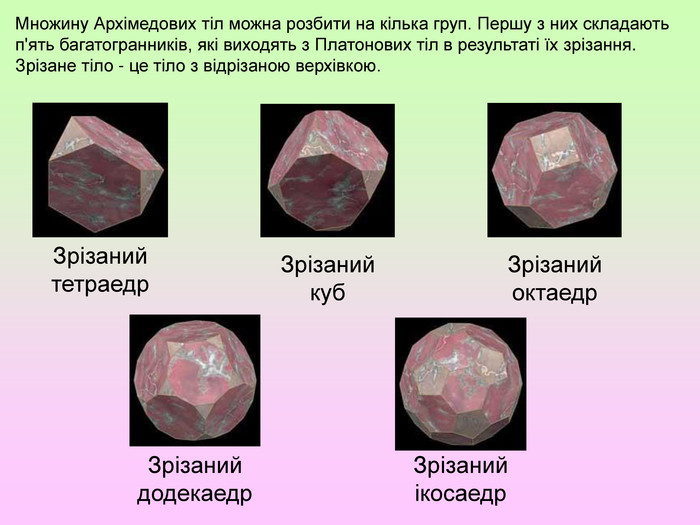
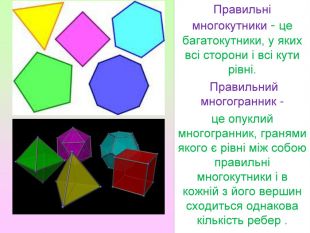
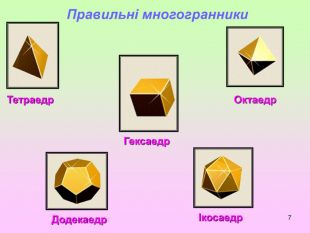
Презентація з геометрії для 11 класу "Правильні і напівправильні многогранники"
Про матеріал
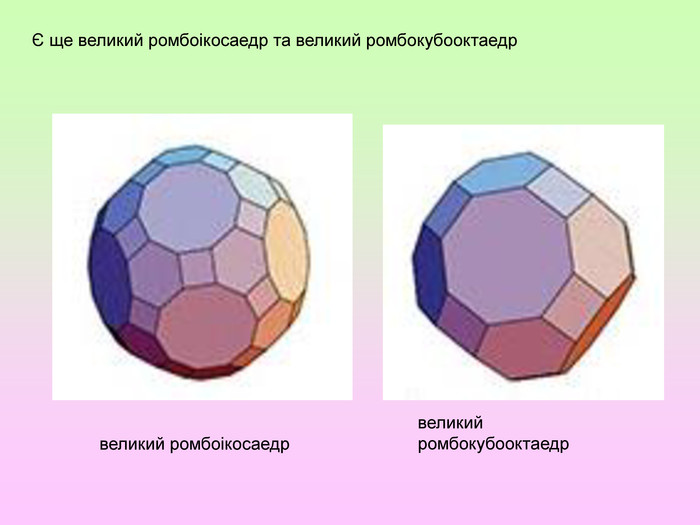
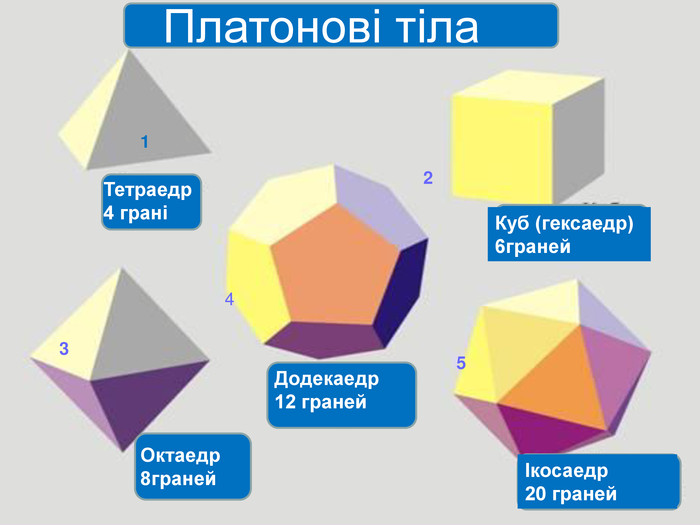
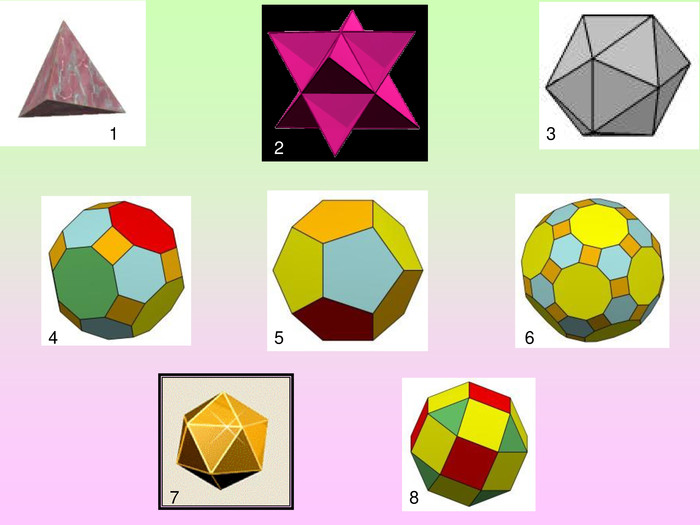
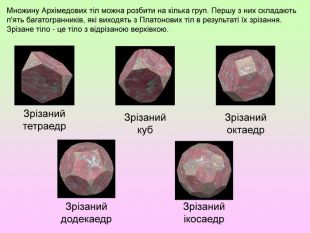
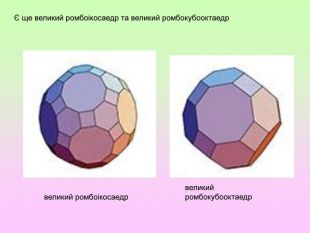
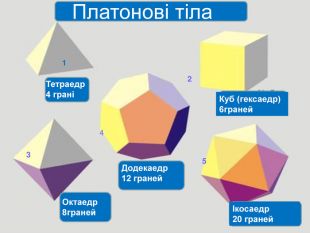
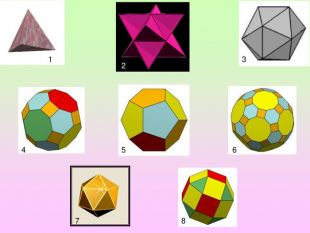
Презентація з геометрії для 11 класу "Правильні і напівправильні многогранники" знайомить учнів з тілами Архімеда та
Платоновими тілами.Можна використати як на уроці, так і в позакласній роботі.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
-
-
Ознайомлю дітей на факультативі!
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку