Презентація з теми: "Лінійні рівняння з двома змінними"
Про матеріал
Зміст уроку:
1. Що таке лінійне рівняння з двома змінними.
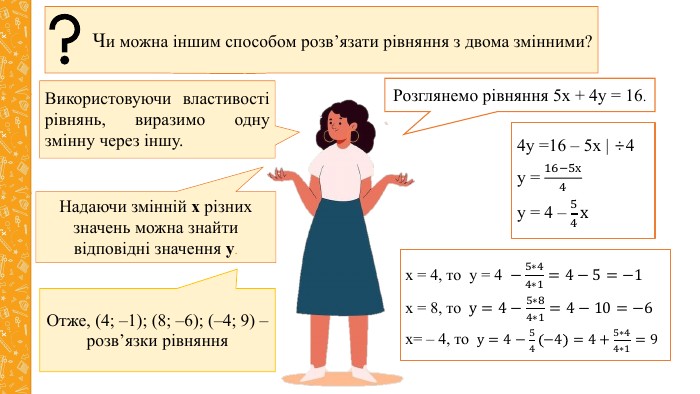
2. Що є розв’язком лінійного рівняння з двома змінними.
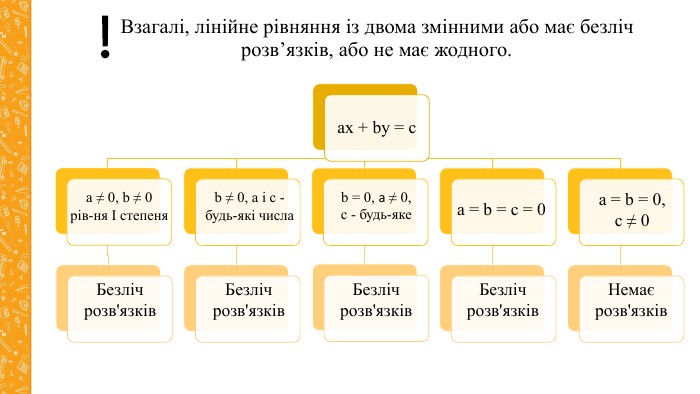
3. Окремі випадки лінійних рівнянь з двома змінними.
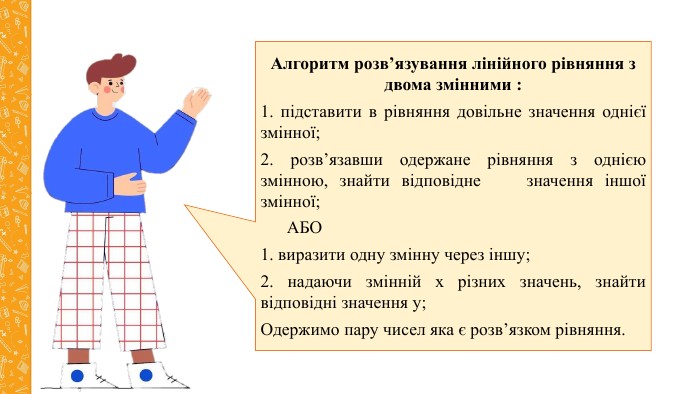
4. Алгоритм розв’язування лінійного рівняння з двома змінними.
Обов'язково запустіть презентації (F5), бо вона інтерактивна!
Також до презентації є конспект до уроку, який також можна завантажити окремим файлом. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку