Презентація за темою :"Квадратний тричлен.Розкладання квадратного тричлена на множники.
Про матеріал
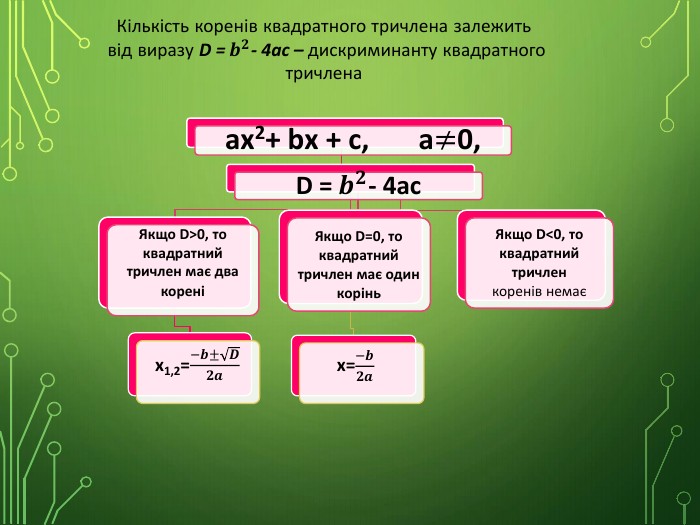
Презентація до уроку алгебри з теми "Квадратний тричлен. Розкладання квадратного тричлена на множники". Мета уроку: домогтися засвоєння поняття квадратного тричлена, коренів квадратного тричлена; сформувати вміння виконувати розкладання квадратного тричлена на множники
Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 8 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
До уроку
§ 3. Квадратні рівняння Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку