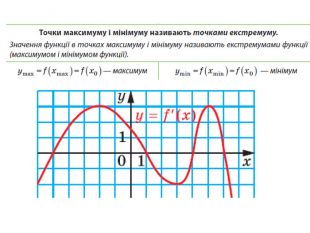
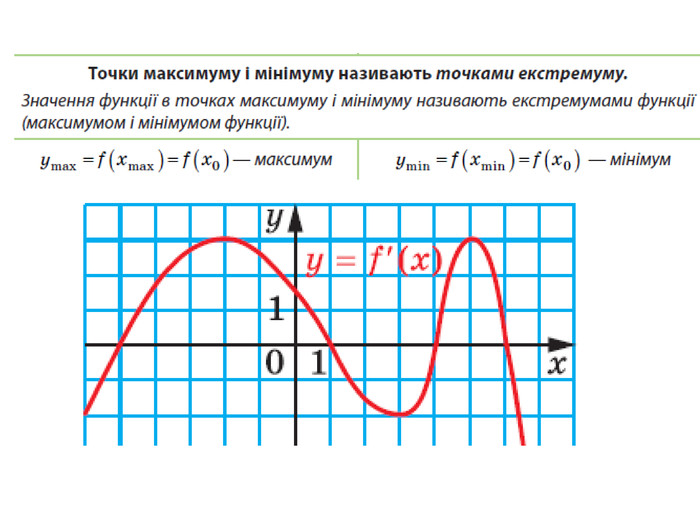
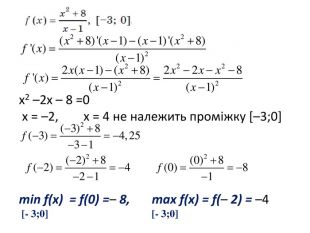Презентація за темою: "Найбільше та найменше значення функції"

Найбільше і найменше значення функції

у’= – 2x +6– 2x +6 = 0– 2x = – 6 x = 33+- f(x) зростає на f(x) спадає на ymax =f(xmax) = – 32 + 6∙3 – 5 = 4 екстремум функції, максимум функції точка екстремуму, точка максимуму

Яку кількість продукції треба випустити підприємству, щоб отримати найбільший прибуток? Як, маючи обмежені ресурси, ви-конати виробниче завдання в найкоротший час? Як організувати доставку товару в торговельні точки так, щоб витрати палива були найменшими? Такі й подібні задачі на пошук оптимального розв’язку займають значне місце в практичній діяльності людини.

Знайдіть найбільше і найменше значення функції на вказаному проміжку f ’(x) = 6x – 3x2 6x – 3x2 = 0 3x(2 – x) = 0x = 0, x =2f (- 1) = 3(– 1)2 – (– 1)3 =3 – (– 1) = 4f (0) = 3(0)2 – (0)3 = 0f (2) = 3(2)2 – (2)3 = 4f (3) = 3(3)2 – (3)3 =0 min f(x) = 0, max f(x) = 4 [- 1;3] [- 1;3]

f ’(x) = 4x3 – 4x4x3 – 4x = 0 4x(x2 –1) = 0 4x(x –1)(x +1) = 0 x = 0, x =– 1, x = 1x =– 1 не належить проміжку [0;2]f (0) = 5f (1) = 14 – 2∙12 + 5 = 4f (2) = 24 – 2∙22 + 5 = 13 min f(x) = f(1) = 4, max f(x) = f(2) = 13 [0;2] [0;2]

x2 –2x – 8 =0 x = –2, x = 4 не належить проміжку [–3;0] min f(x) = f(0) =– 8, max f(x) = f(– 2) = –4 [- 3;0] [- 3;0]

x2 =16 x = 4, x = –4 не належить проміжку [1;6]f(1) = 2 , f(4) =0,5 + 0,5 =1, f(6) =3/4 + 1/3=13/12min f(x) = f(4) = 1, max f(x) = f(1) = 2 [1;6] [1;6] [1;6] 1818

Подайте число 8 у вигляді суми двох таких невід’ємних чисел, щоб добуток одного із цих чисел і куба другого числа був найбільшим.х – одне число, (8 – х) – друге числоf(x)=(8 – х)х3 [0;8] f(x)= 8х3 – х4f’(x)=24x 2 – 4х324x 2 – 4х3 = 04x2 (6– х) = 0x = 0 x = 6f(0)= 0, f(6)= (8 – 6)63 =432, f(8)= 0 Відповідь: 8 = 6 + 2

Подайте число 180 у вигляді суми трьох невід’ємних доданків так, щоб два з них відносились як 1 : 2, а добуток усіх трьохдоданків був найбільшим.х – одне число, 2х – друге, (180 – х – 2х) – третєf(x)=х2х(180 – 3х) [0;180] f(x)= 2х2 (180 – 3х)=360х2 – 6х3f’(x)=720x – 18х2720x – 18х2 = 018x (40– х) = 0x = 0 x = 40f(0)= 0, f(40)= 3200 (180 – 120) >0, f(180)< 0 Відповідь: 180 = 40 + 80 + 60

Дом. завдання: знайти найбільше і найменше значення функції на вказаних проміжках1) f (x) = x3– 6x2 + 2, [–1;2] 2)3) [0;4] 4) Подайте число 12 у вигляді суми двох таких невід’ємних чисел, щоб добуток квадрата одного із цих чисел і подвоєногодругого числа був найбільшим.