Презентація Задачі на рівнобедрений трикутник
Про матеріал
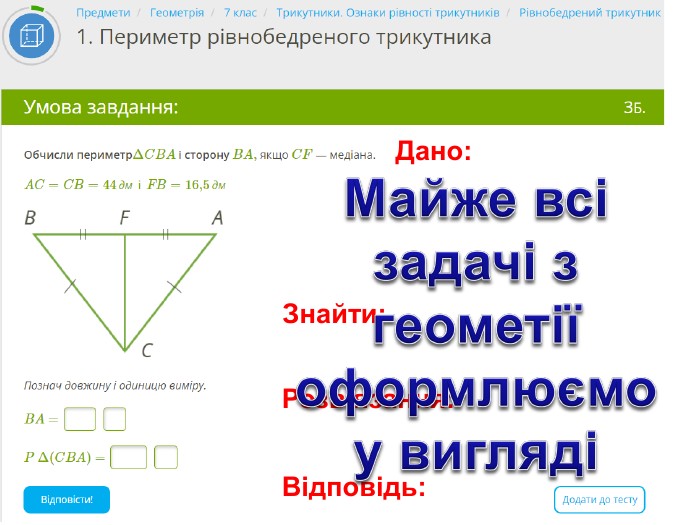
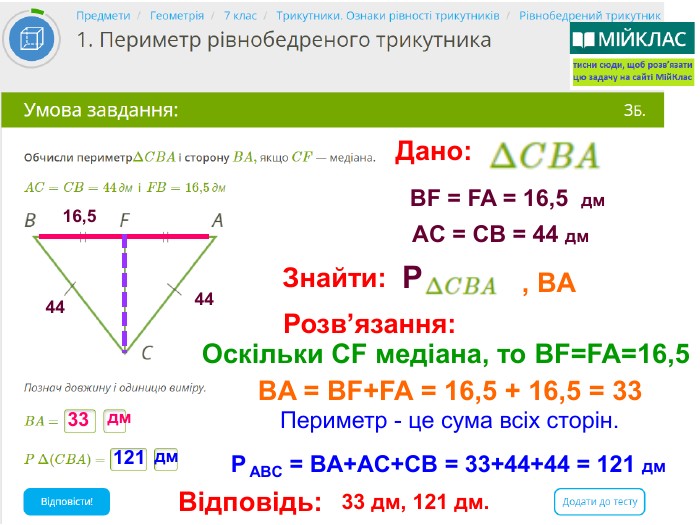
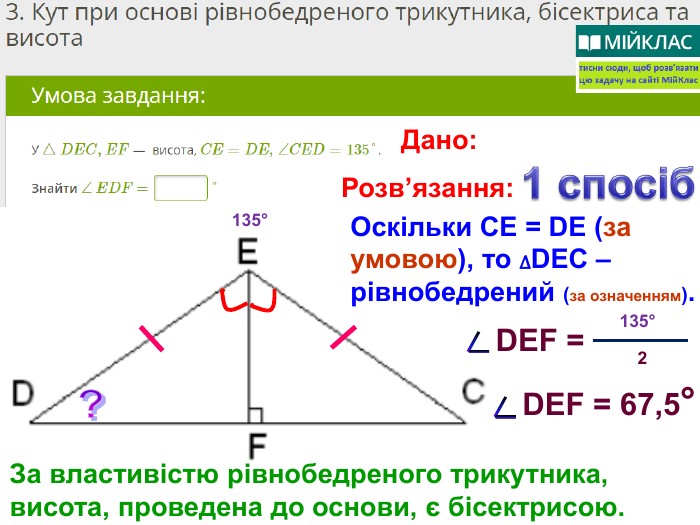
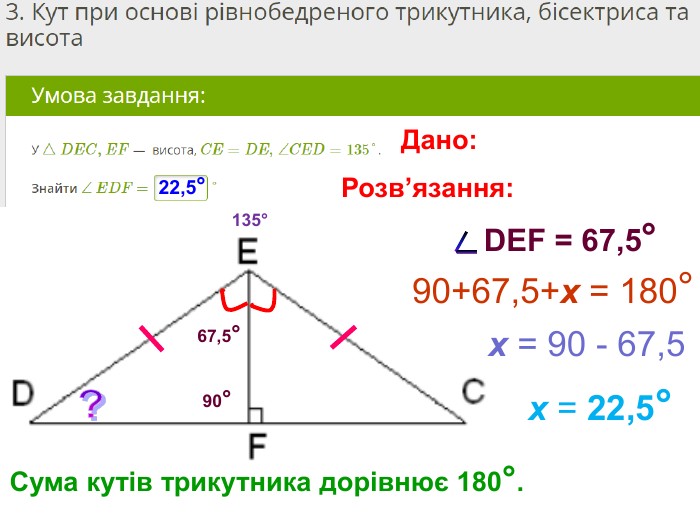
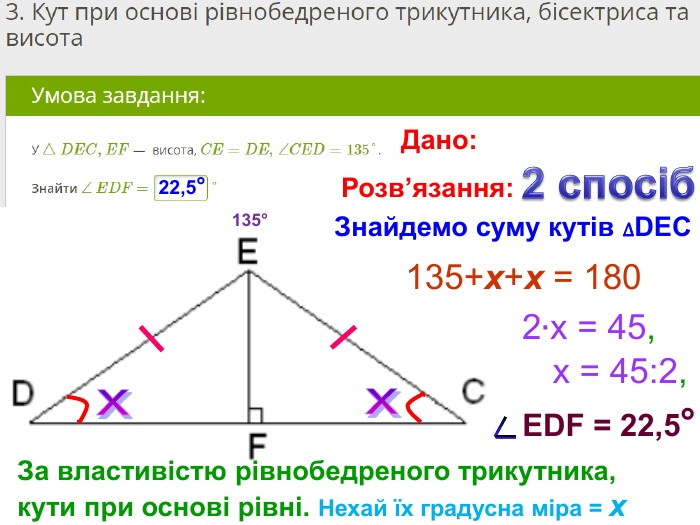
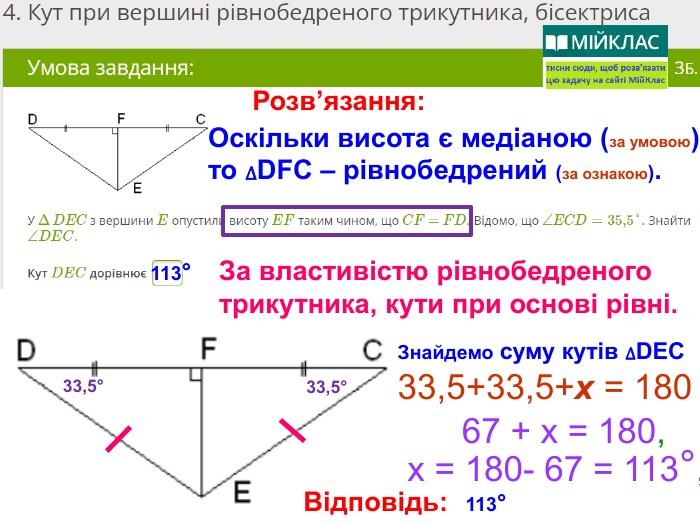
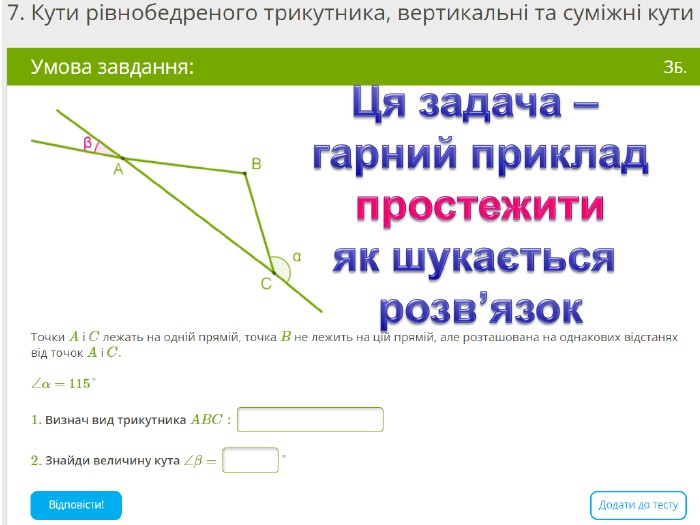
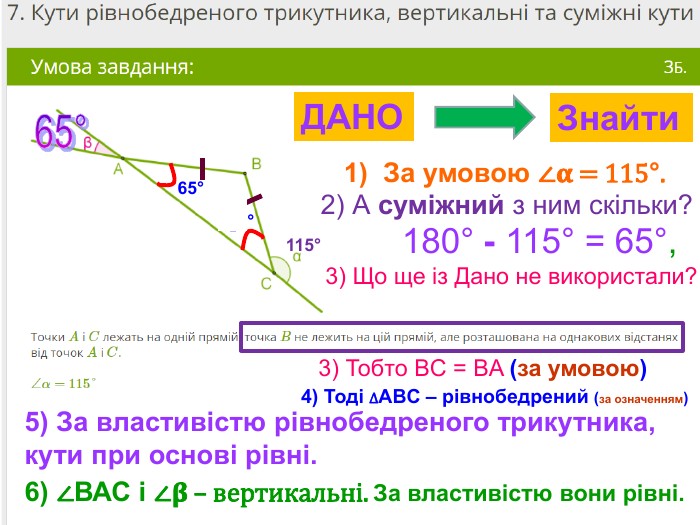
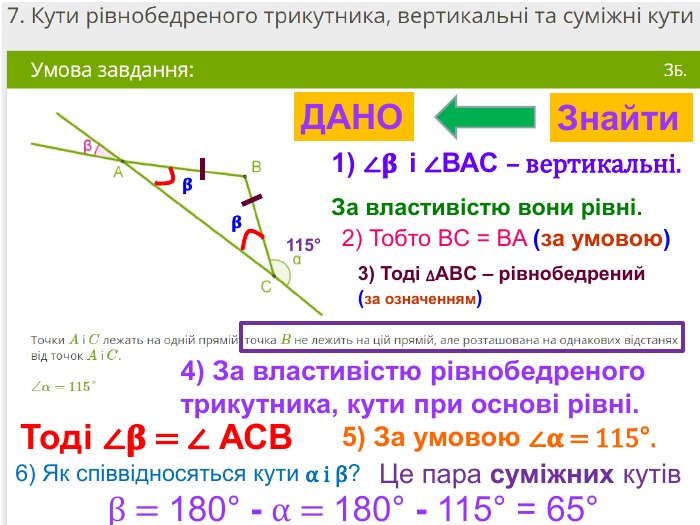
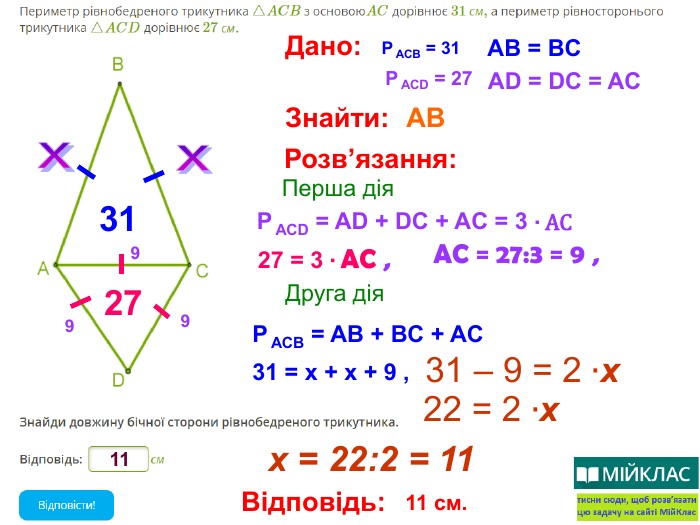
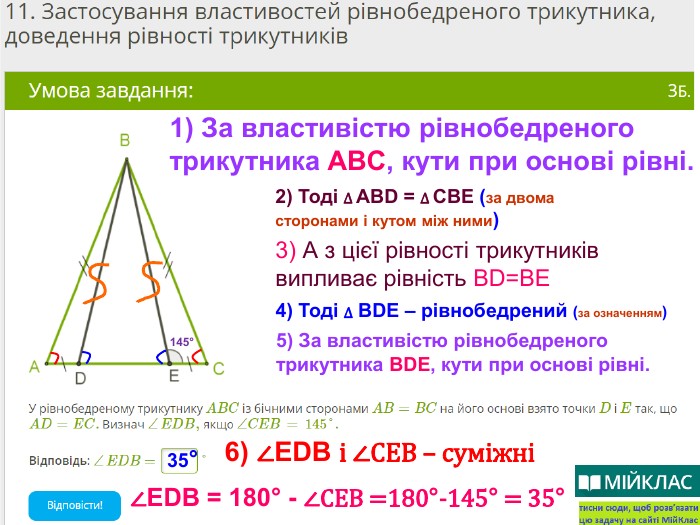
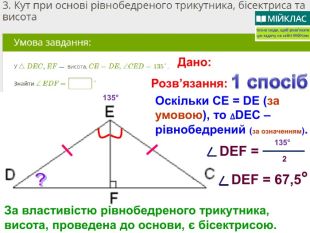
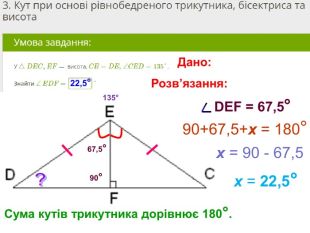
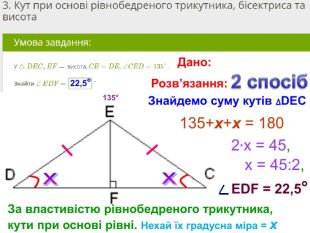
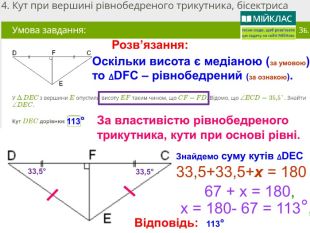
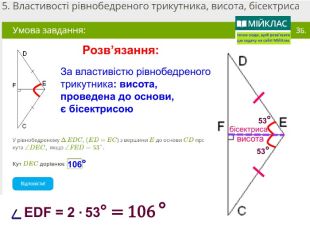
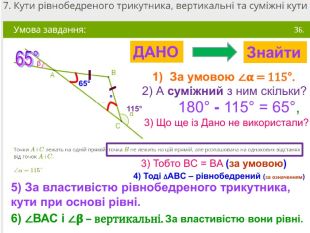
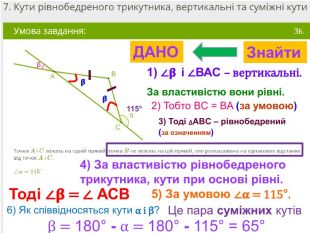
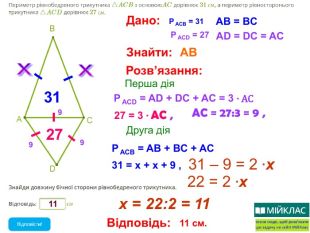
Презентація, в якій показано розв’язання 10 задач, взятих із сайту Мій Клас, на використання властивостей рівнобедреного трикутника. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку