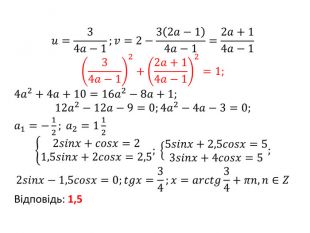Презентація "Задачі з параметрами"
Про матеріал
Презентація містить приклади основних методів розв'язування задач з параметрами: графічний, використання властивостей функцій. Розглянуто завдання ІІІ частини ЗНО Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


![Область визначення. Розв'язати рівняння: 𝑥2𝑥2−11−𝑥2=𝑎 Розв'язання: 𝑥≤1 – область визначення тригонометричних функцій 𝑦=𝑠𝑖𝑛𝑥,𝑦=𝑐𝑜𝑠𝑥 Підстановка: 𝒙=𝒄𝒐𝒔𝒕, 𝑡∈[0;𝜋]𝑐𝑜𝑠𝑡∙2𝑐𝑜𝑠2𝑡−11−𝑐𝑜𝑠2𝑡=𝑎 𝑐𝑜𝑠𝑡∙𝑐𝑜𝑠2𝑡∙𝑠𝑖𝑛𝑡=𝑎 ∙4 1−𝑐𝑜𝑠2𝑡=𝑠𝑖𝑛𝑡=𝑠𝑖𝑛𝑡, 𝑡∈[0;𝜋]𝑠𝑖𝑛4𝑡=4𝑎⇒𝑎∈−14 ;14 Область визначення. Розв'язати рівняння: 𝑥2𝑥2−11−𝑥2=𝑎 Розв'язання: 𝑥≤1 – область визначення тригонометричних функцій 𝑦=𝑠𝑖𝑛𝑥,𝑦=𝑐𝑜𝑠𝑥 Підстановка: 𝒙=𝒄𝒐𝒔𝒕, 𝑡∈[0;𝜋]𝑐𝑜𝑠𝑡∙2𝑐𝑜𝑠2𝑡−11−𝑐𝑜𝑠2𝑡=𝑎 𝑐𝑜𝑠𝑡∙𝑐𝑜𝑠2𝑡∙𝑠𝑖𝑛𝑡=𝑎 ∙4 1−𝑐𝑜𝑠2𝑡=𝑠𝑖𝑛𝑡=𝑠𝑖𝑛𝑡, 𝑡∈[0;𝜋]𝑠𝑖𝑛4𝑡=4𝑎⇒𝑎∈−14 ;14](/uploads/files/334031/92133/98128_images/2.jpg)


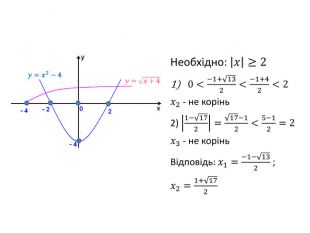
![Необхідно, щоб один із коренів належав відрізку [0; 3], а інший – ні.1) 0≤𝑎+2≤3𝑎−1<0;𝑎−1>3𝑎∈[−2;1) 2) 0≤𝑎−1≤3𝑎+2<0;𝑎+2>3 𝑎∈(1;4] Відповідь: 𝑎∈[−2;1)∪(1;4] Необхідно, щоб один із коренів належав відрізку [0; 3], а інший – ні.1) 0≤𝑎+2≤3𝑎−1<0;𝑎−1>3𝑎∈[−2;1) 2) 0≤𝑎−1≤3𝑎+2<0;𝑎+2>3 𝑎∈(1;4] Відповідь: 𝑎∈[−2;1)∪(1;4]](/uploads/files/334031/92133/98128_images/5.jpg)






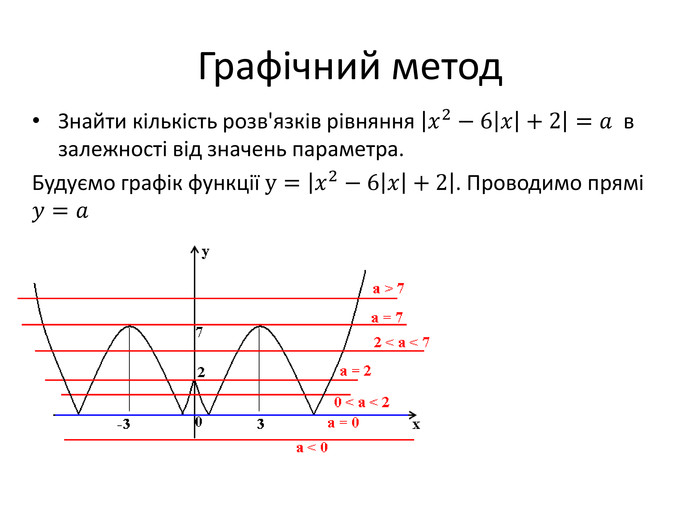
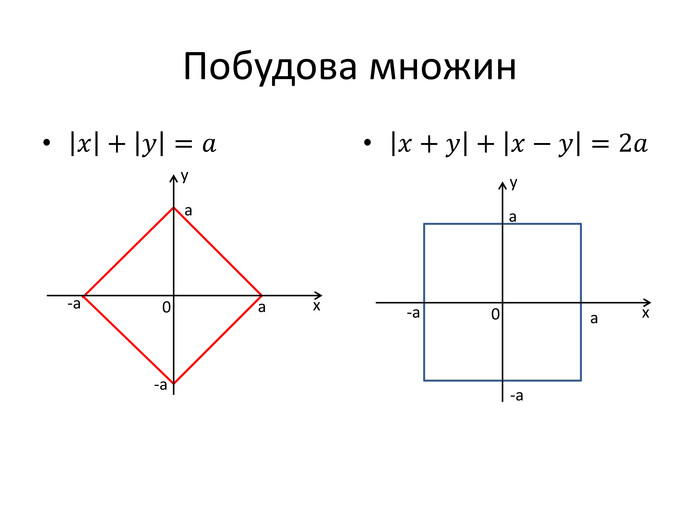





![(2015) При яких значеннях параметра 𝑎 рівняння 𝑥2−2𝑎+1𝑥+6𝑎−3𝑡𝑔𝜋𝑥−1449𝑥2−84𝑥𝑎+36𝑎2=0 на проміжку [0; 1] має рівно два різні корені? Знаменник: 449𝑥2−84𝑥𝑎+36𝑎2=47𝑥−6𝑎2=|7𝑥−6𝑎| Розглянемо рівняння: 𝑡𝑔𝜋𝑥−1=0;𝑡𝑔𝜋𝑥=1;𝑥=14+𝑛, 𝑛∈𝑍. Корінь 𝑥=14 належить данному відрізку за умови 6𝑎−74≠0, 𝑎≠724 Квадратичне рівняння 𝑥2−2𝑎+1𝑥+6𝑎−3=0. 𝐷4=(𝑎+1)2−6𝑎+3=(𝑎−2)2 . 𝑥1=𝑎+1−𝑎+2=3; 𝑥2=𝑎+1+𝑎−2=2𝑎−1 Необхідно, щоб 0≤2𝑎−1≤1⇒12≤𝑎≤1. Обмеження: 2𝑎−1≠142𝑎−1≠67𝑎 ; 𝑎≠58𝑎≠78 Відповідь: 𝑎∈12 ; 58∪58 ; 78∪78 ; 1 (2015) При яких значеннях параметра 𝑎 рівняння 𝑥2−2𝑎+1𝑥+6𝑎−3𝑡𝑔𝜋𝑥−1449𝑥2−84𝑥𝑎+36𝑎2=0 на проміжку [0; 1] має рівно два різні корені? Знаменник: 449𝑥2−84𝑥𝑎+36𝑎2=47𝑥−6𝑎2=|7𝑥−6𝑎| Розглянемо рівняння: 𝑡𝑔𝜋𝑥−1=0;𝑡𝑔𝜋𝑥=1;𝑥=14+𝑛, 𝑛∈𝑍. Корінь 𝑥=14 належить данному відрізку за умови 6𝑎−74≠0, 𝑎≠724 Квадратичне рівняння 𝑥2−2𝑎+1𝑥+6𝑎−3=0. 𝐷4=(𝑎+1)2−6𝑎+3=(𝑎−2)2 . 𝑥1=𝑎+1−𝑎+2=3; 𝑥2=𝑎+1+𝑎−2=2𝑎−1 Необхідно, щоб 0≤2𝑎−1≤1⇒12≤𝑎≤1. Обмеження: 2𝑎−1≠142𝑎−1≠67𝑎 ; 𝑎≠58𝑎≠78 Відповідь: 𝑎∈12 ; 58∪58 ; 78∪78 ; 1](/uploads/files/334031/92133/98128_images/19.jpg)


![(2014) При якому найбільшому значенні параметра система 2𝑎−1𝑠𝑖𝑛𝑥+𝑐𝑜𝑠𝑥=2𝑎𝑠𝑖𝑛𝑥+2𝑎−1𝑐𝑜𝑠𝑥=𝑎+1 має безліч розв'язків ? 𝑠𝑖𝑛𝑥=𝑢;𝑐𝑜𝑠𝑥=𝑣;𝑢,𝑣∈[−1;1]!!! 𝑢2+𝑣2=12𝑎−1𝑢+𝑣=2 ∙(2𝑎−1)𝑎𝑢+2𝑎−1𝑣=𝑎+1(2𝑎−1)2𝑢−𝑎𝑢=3𝑎−3;𝑢=3(𝑎−1)(𝑎−1)(4𝑎−1) Якщо 𝑎=1, то з першого рівняння системи маємо: 𝑠𝑖𝑛𝑥+𝑐𝑜𝑠𝑥=2 немає розв'язків (2014) При якому найбільшому значенні параметра система 2𝑎−1𝑠𝑖𝑛𝑥+𝑐𝑜𝑠𝑥=2𝑎𝑠𝑖𝑛𝑥+2𝑎−1𝑐𝑜𝑠𝑥=𝑎+1 має безліч розв'язків ? 𝑠𝑖𝑛𝑥=𝑢;𝑐𝑜𝑠𝑥=𝑣;𝑢,𝑣∈[−1;1]!!! 𝑢2+𝑣2=12𝑎−1𝑢+𝑣=2 ∙(2𝑎−1)𝑎𝑢+2𝑎−1𝑣=𝑎+1(2𝑎−1)2𝑢−𝑎𝑢=3𝑎−3;𝑢=3(𝑎−1)(𝑎−1)(4𝑎−1) Якщо 𝑎=1, то з першого рівняння системи маємо: 𝑠𝑖𝑛𝑥+𝑐𝑜𝑠𝑥=2 немає розв'язків](/uploads/files/334031/92133/98128_images/22.jpg)

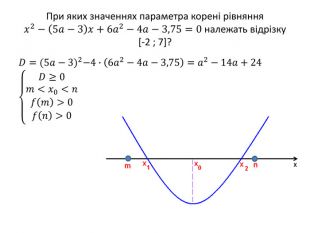
![При яких значеннях параметра корені рівняння 𝑥2−2𝑎+1𝑥−3𝑎2+7𝑎−2=0 належать відрізку [-2 ; 7]? 𝐷=(2𝑎+1)2−4∙−3𝑎2+7𝑎−2=16𝑎2−24𝑎+9=(4𝑎−3)2 𝑥1=2𝑎+1−4𝑎+32=−𝑎+2 ;𝑥2=2𝑎+1+4𝑎−32=3𝑎−1 −2≤−𝑎+2≤7−2≤3𝑎−1≤7 ; −5≤𝑎≤4−13≤𝑎≤83 Відповідь: 𝑎∈−13;83 При яких значеннях параметра корені рівняння 𝑥2−2𝑎+1𝑥−3𝑎2+7𝑎−2=0 належать відрізку [-2 ; 7]? 𝐷=(2𝑎+1)2−4∙−3𝑎2+7𝑎−2=16𝑎2−24𝑎+9=(4𝑎−3)2 𝑥1=2𝑎+1−4𝑎+32=−𝑎+2 ;𝑥2=2𝑎+1+4𝑎−32=3𝑎−1 −2≤−𝑎+2≤7−2≤3𝑎−1≤7 ; −5≤𝑎≤4−13≤𝑎≤83 Відповідь: 𝑎∈−13;83](/uploads/files/334031/92133/98128_images/24.jpg)
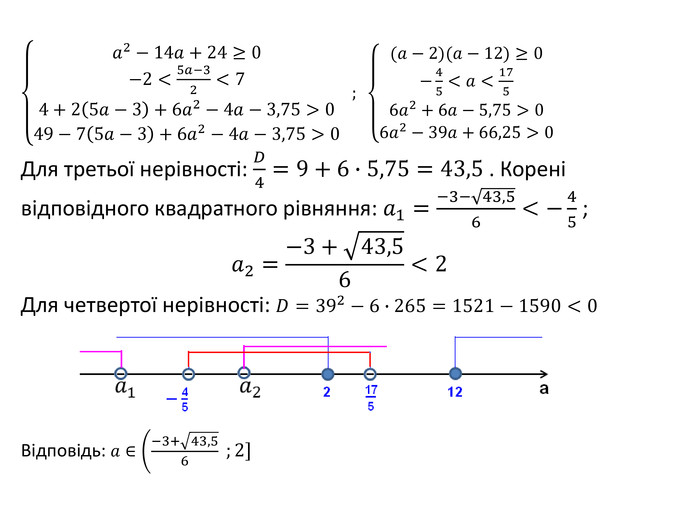
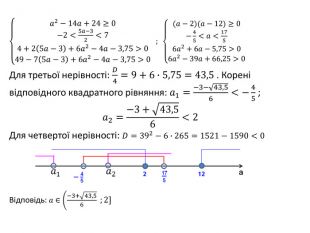
![При яких значеннях параметра корені рівняння 𝑥2−5𝑎−3𝑥+6𝑎2−4𝑎−3,75=0 належать відрізку [-2 ; 7]? 𝐷=(5𝑎−3)2−4∙6𝑎2−4𝑎−3,75=𝑎2−14𝑎+24𝐷≥0𝑚<𝑥0<𝑛𝑓𝑚>0𝑓𝑛>0 При яких значеннях параметра корені рівняння 𝑥2−5𝑎−3𝑥+6𝑎2−4𝑎−3,75=0 належать відрізку [-2 ; 7]? 𝐷=(5𝑎−3)2−4∙6𝑎2−4𝑎−3,75=𝑎2−14𝑎+24𝐷≥0𝑚<𝑥0<𝑛𝑓𝑚>0𝑓𝑛>0](/uploads/files/334031/92133/98128_images/25.jpg)