Презентація "ЗАСТОСУВАННЯ ПОХІДНОЇ ДЛЯ РОЗВ'ЯЗУВАННЯ ЗАДАЧ НА ОПТИМІЗАЦІЮ"
Про матеріал
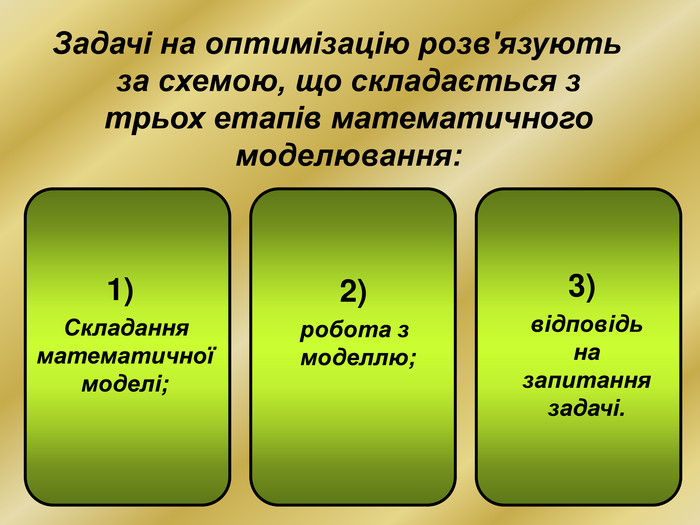
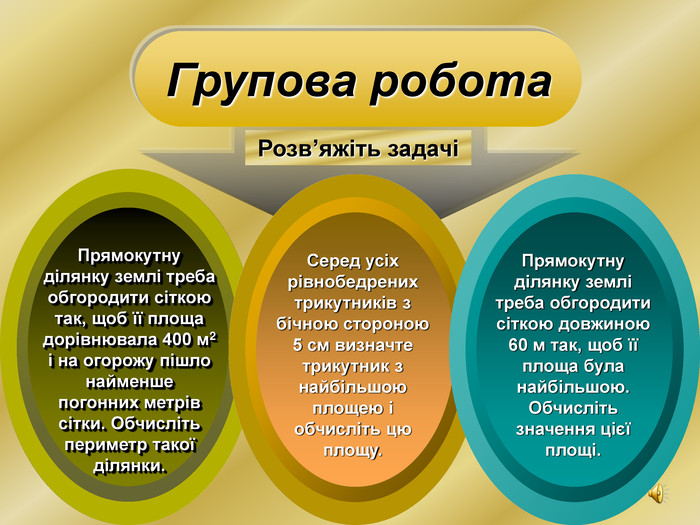
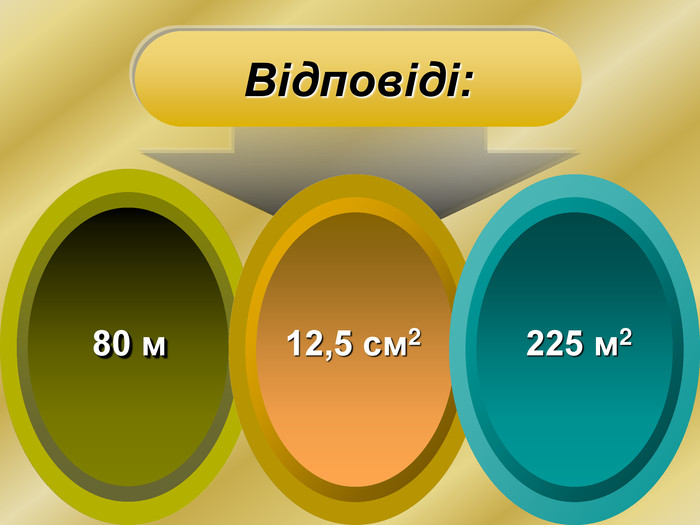
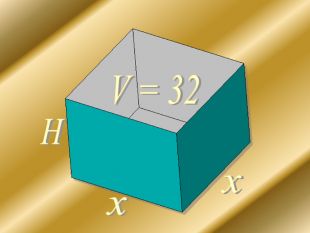
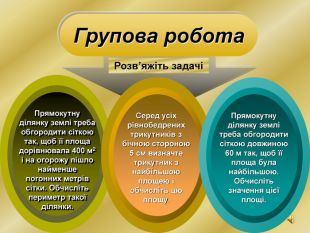
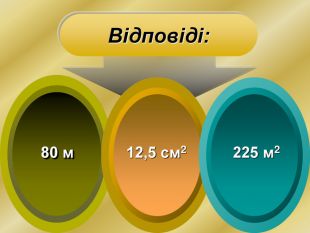
Презентація призначена для використання на уроках алгебри для формування в учнів вміння застосовувати знання з теми "Похідна" для розв'язування прикладних задач. При мінімальній кількості годин математики у 10 класі можна запропонувати учням опрацювати даний матеріал самостійно. Презентація містить музичний супровід, який, при бажанні можна приглушити, чи відключити на пристрої. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую, дуже якісний контент.
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку