Презентація "Властивості тригонометричних функцій!
Про матеріал
Опис та розбір загальних властивостей тригонометричних функцій, а саме: множина значень, область визначення, парність, періодичність, знаки за одиничним колом. Висвітлено блок формул, які доцільно використовувати в дані темі.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
Дякую за роботу
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




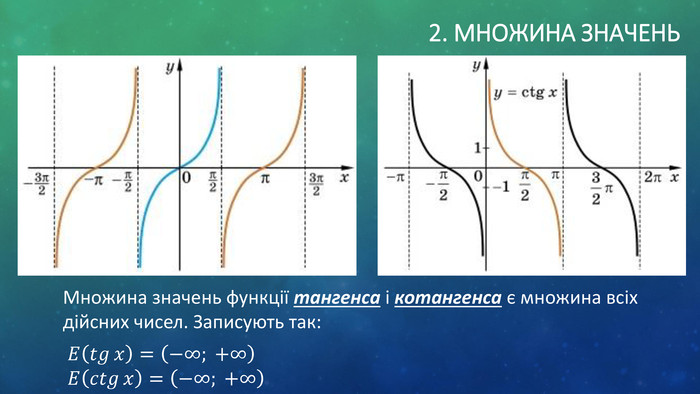
![2. Множина значень. Множиною значень функції синуса та косинуса є проміжок [-1;1]. Це можна записати так: 𝐸sin𝑥=−1;1 𝐸cos𝑥=−1;1 2. Множина значень. Множиною значень функції синуса та косинуса є проміжок [-1;1]. Це можна записати так: 𝐸sin𝑥=−1;1 𝐸cos𝑥=−1;1](/uploads/files/188961/229072/245054_images/4.jpg)