Урок . "Степенева функція . Побудова графіків в Microsoft Excel"

Про матеріал

Інтегрований урок алебри та інформатики. Учні мають можливість дослідити властивості степеневої функції, вдосконалити навички побудови графіків в Microsoft Excel , навчаються працювати в групі.

Перегляд файлу

Тема. Степенева функція . Побудова графіків в Microsoft Excel

Інтегрований урок з алгебри та інформатики

Мета: сформувати поняття степеневої функції, познайомити учнів з її властивостями , графіком , вдосконалювати навички побудови графіків Продемонструвати можливості застосування Microsoft Excel для обчислень, побудов графіків . Розвивати творчі здібності учнів, логічне мислення та спрямувати увагу на виконанні завдань при побудові графіків. Виховувати вміння працювати в групі, виховувати інтерес до навчання.

Тип уроку: комбінований

Обладнання: ПК з відповідним програмним забезпеченням, роздатковий матеріал ,картки із завданням), інтерактивна дошка.

Хід уроку.

І Перевірка домашнього завдання.

Усні вправи. 1.Обчисліть: ³√8 , ⁴√81,⁵√-1, ³√-27.

2. Подайте вирази у вигляді степеня з раціональним показником:

√2 ,³√6 , 1/⁷√2 , ⁵√1/х².

3. Обчисліть: 9^1/2 , 27^1/3 , 8^2/3 , 81^3/4.

4.Розв’язати ірраціональне рівняння √15-х + √3-х =6.

Клас ділиться на 3 рівносильні групи.

1 група : способом піднесення до степеня.

2 група: способом зведення до системи ірраціональних рівнянь.

3 група : помноживши обидві частини рівняння на вираз , спряжений лівій частині.

ІІ. Актуалізація опорних знань.

Ми з вами вивчали різні функції, будували графіки , вивчали їх властивості. Давайте згадаємо які властивості функцій ми знаємо. Для цього кожна група нехай на даному аркуші запишуть відомі їм властивості функцій.

Представник групи , яка перша справилася з завданням , зачитує властивості функцій , які вони пригадали. Представники інших груп доповнюють властивості , які були упущені.Потім відкриваєм бічну дошку, щоб учні перевірили чи всі вивчені властивості функцій вони згадали.

Запис на дошці:

Область визначення.
Область значень.
Точки перетину з осями координат.
Парність , непарність.
Проміжки знакосталості.
Проміжки зростання і спадання функції.
Найбільше і найменше значення функції.

ІІІ Вивчення нового матеріалу.

Степеневою функцією називається функція виду у = х^p, де р — постійне дійсне число, а х (основа) — змінна.

Які з наступних функцій будуть степеневими?

у=х⁴ , у=3х^{5 ,} у=( х+1,43)² , у=х^√3 , у=1\х , у= 4^х , у=√х .

Пригадаємо властивості степеневих функцій та їх графіки які ви вивчали раніше та дослідимо нові властивості .

Результати наших досліджень будемо записувати до таблиці.

Таблиця результатів досліджень

Графік функції

Властивості функцій

У= х²

У= х⁶

У= х¹⁰

У= х

У= х ³

У= х ⁷

У= х^-1

У= х ^-3

У= х ^–7

У= х ^-2

У= х ^-6

У= х ^-10

У= х ^1/2

У= х ^1/3

У= х ^1/4

Р- парне натуральне число

Р- непарне число

Р- ціле непарне від’ємне число

Р- ціле парне від’ємне число

Р= 1/к , де к- натуральне число

На уроках інформатики для обчислень функцій та побудов графіків ви застосувували Microsoft Excel . Сьогодні ці ваші вміння допоможуть нам при дослідженні властивостей степеневої функції.

Побудуємо в середовищі Microsoft Excel графіки кожної групи та запишемо їх властивості за поданою схемою.

Область визначення.
Область значень.
Точки перетину з осями координат.
Парність , непарність.
Проміжки знакосталості.
Проміжки зростання і спадання функції.
Найбільше і найменше значення функції

На допомогу вам прийде алгоритм побудови графіка функції.(Додаток 2)

(Учні , сідаючи за комп’ютери , утворюють міні – групи по 2- 3 чоловіка. На робочому столі комп’ютерів вони відкривають Microsoft Excel

Учні будують графіки функцій , які задані в таблиці . Після побудови кожної групи графіків учні записують властивості даних функцій у таблицю. )

Релаксація (в ході роботи за комп’ютером)

Вправи для зняття втоми м’язів та очей.

Для покращення фокусування ока подивитись на кінчик носа, потім одразу перевести погляд у далечінь. В обох випадках погляд затримати на кілька секунд. Повторити вправу 4-5 разів.

Заплющити очі на 3-5 секунд, а потім розплющити їх на такий же час. Повторити вправу 4-5 разів.

Після завершення роботи на екран для преревірки проєктується таблиця досліджень , пропущені дані досліджуємо колективно. (Додаток 1)

Таблиця результатів досліджень

Графік функції

Властивості функцій

У= х²

У= х⁶

У= х¹⁰

У= х

У= х ³

У= х ⁷

У= х^-1

У= х ^-3

У= х ^–7

У= х ^-2

У= х ^-6

У= х ^-10

У= х ^1/2

У= х ^1/3

У= х ^¼

Р- парне натуральне число

1.D(y)=R

2. E(y)=[0;1)

3.(0;0)

4.Парна.

5.у>0 при хє(-∞; 0)U( 0; ∞)

6.Зростає при хє (-∞; 0] , спадає при хє [ 0; ∞).

7. Х_min=0, найменше значення –0.

Р- непарне число

1.D(y)=R,

2. E(y)=R

3.(0;0)

4.Непарна.

5.у<0 при хє(-∞; 0) , у>0 при хє ( 0; ∞)

6.Зростає при хє R

7. Не має.

Р- ціле непарне від’ємне число

1.D(y)= (-∞; 0)U( 0; ∞)

2. E(y)= (-∞; 0)U( 0; ∞)

3. Немає.

4.Непарна.

5.у>0 при хє ( 0; ∞) , у<0 при хє(-∞; 0)

6. Зростає при хє(-∞; 0)U( 0; ∞)

7. Не має.

Р- ціле парне від’ємне число

1.D(y)= (-∞; 0)U( 0; ∞)

2. E(y)= ( 0; ∞)

3. Немає.

4.Парна.

5.у>0 при хє(-∞; 0)U( 0; ∞) , у<0 не має.

6.Зростає при хє ( 0; ∞) , спадає при хє(-∞; 0)

Р= 1/к , де к- натуральне число

ІV Самостійна робота.

Кожна міні – група отримує картку.

-Побудувати графіки функцій

у= х ^-4 та у=х^1.5 і порівняти їх властивості.

- Побудувати графіки функцій

у= х^-5 та у=х⁸ і порівняти їх властивості.

- Побудувати графіки функцій

у= х ^-4 та у=х⁴ і порівняти їх властивості.

V Підсумок уроку.

- Які функції ми сьогодні вивчали?

- Дайте означення степеневої функції.

- Від чого залежить графік і властивості степеневої функції?

- За допомогою якої програми ми будували графіки степеневих функцій?

VІ Домашнє завдання.

1 Установіть відповідність між функціями,заданими формулами (1–4), та їхніми властивостями (А–Д).

1	y =x ⁹	А	Функція спадає на проміжку (- + 1; ∞)
2	y= x^-12	Б	Областю визначення функції є проміжок (-∞; 1 - ]
3	y=( x + 1)^-3/4	В	Множиною значень функції є проміжок [0;+ ∞)
4	y =(x + 1)^1,2	Г	Парна функція
		Д	Непарна функція

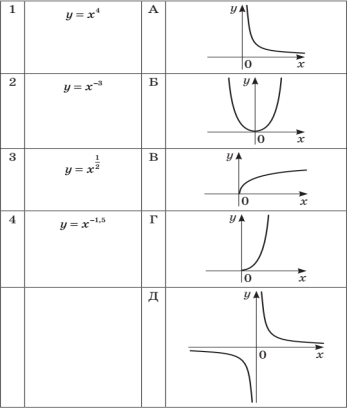
2 Установіть відповідність між функціями (1–4) та ескізами їхніх графіків (А–Д).

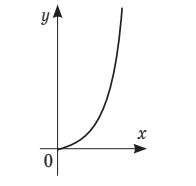
3 Графік якої з наведених нижче функцій зображено на рисунку?

Додаток 1

Таблиця результатів досліджень

Графік функції

Властивості функцій

У= х²

У= х⁶

У= х¹⁰

У= х

У= х ³

У= х ⁷

У= х^-1

У= х ^-3

У= х ^–7

У= х ^-2

У= х ^-6

У= х ^-10

У= х ^1/2

У= х ^1/3

У= х ^¼

Р- парне натуральне число

1.D(y)=R

2. E(y)=[0;1)

3.(0;0)

4.Парна.

5.у>0 при хє(-∞; 0)U( 0; ∞)

6.Зростає при хє (-∞; 0] , спадає при хє [ 0; ∞).

7. Х_min=0, найменше значення –0.

Р- непарне число

1.D(y)=R,

2. E(y)=R

3.(0;0)

4.Непарна.

5.у<0 при хє(-∞; 0) , у>0 при хє ( 0; ∞)

6.Зростає при хє R

7. Не має.

Р- ціле непарне від’ємне число

1.D(y)= (-∞; 0)U( 0; ∞)

2. E(y)= (-∞; 0)U( 0; ∞)

3. Немає.

4.Непарна.

5.у>0 при хє ( 0; ∞) , у<0 при хє(-∞; 0)

6. Зростає при хє(-∞; 0)U( 0; ∞)

7. Не має.

Р- ціле парне від’ємне число

1.D(y)= (-∞; 0)U( 0; ∞)

2. E(y)= ( 0; ∞)

3. Немає.

4.Парна.

5.у>0 при хє(-∞; 0)U( 0; ∞) , у<0 не має.

6.Зростає при хє ( 0; ∞) , спадає при хє(-∞; 0)

Р= 1/к , де к- натуральне число

Додаток 2

Побудова графіків функцій в Microsoft Excel

Операції	Дії користувача
В першому рядку робочого листа набираємо назву функції Записати в комірки А1 і В1 х та у відповідно. Заповнити діапазон А2:А22 числами від *-10* до 10 з кроком 1	І спосіб Записати в А2 число *-10, в А3 число -9, виділити діапазон А2:А3, натиснувши маркер заповнення, протягнути до комірки А22. ІІ спосіб* У комірку А2 ввести -10, Enter, Правка, Заполнить,
Обчислити *значення функції* у діапазоні В2:В22	Виділити комірку В2, у рядок формул ввести =(математичний запис формули) (потрібне нам значення х знаходиться в комірці А2). Скопіювати формулу у комірки діапазону В3:В22
Побудувати *графік* функції	Виділити діапазон А1:В22, (або Вставка, Диаграмма), вибрати Точечная, Далее, в полі Название диаграммы ввести назву функції , Далее, Готово
Додати *лінії сітки*	Диаграмма, Параметры диаграммы, Линии сетки, Основные линии Х та У, ОК
Відформатувати створений графік	Правою клавішею мишки клацнути на лінії графіка, обрати Формат рядов данных, задати колір та товщину лінії Правою клавішею клацнути на сірій області графіка, обрати Формат области построения, обрати Заливка прозрачная Правою клавішею мишки клацнути на білій області діаграми, обрати Формат области диаграммы, Способы заливки, обрати кольори та відповідний тип .