ПРИКЛАДНІ ЗАДАЧІ ПО ПЛАНІМЕТРІЇ ТА СТЕРЕОМЕТРІЇ З ТЕМИ «КОНУС»

ПРИКЛАДНІ ЗАДАЧІ ПО ПЛАНІМЕТРІЇ ТА СТЕРЕОМЕТРІЇ З ТЕМИ «КОНУС»

Задача 1

Картоплю насипали в купу конічної форми. Довжина кола основи купи 12 м, твірна -3м.Скільки тон картоплі знаходиться в купі? Маса 1м³ картоплі 800 кг.

Дано:    конус, С = 12 м, l = 3м.

Знайти:     V_к , m.

Розв’язання:

C = 2R.    R =  Мм.

З  трикутника ОВS за т. Піфагора: м.

Об’єм шукаємо за формулою:

(м³⁾

m = 2,98 · 800 = 2384 кг.

Відповідь:2384 кг картоплі в купі.

Задача 2.

Головна частина ракети, яка повинна входити в щільні шари атмосфери із швидкістю 7900м/с є конусом з кутом розхилу 220 . Скільки матеріалу необхідно на виготовлення цієї частини ракети, якщо її довжина 7,2 м.

По статистиці на Землі щорічно гине від розрядів блискавки 6 чоловік на 1 000 000 жителів( частіше в південних країнах) Цього б не траплялось, якби скрізь були громовідводи, так як утворюється конус безпеки. Чим вище громовідвід, тим більший об’єм такого конуса. Деякі люди намагаються під деревом, але дерево не провідник, на ньому заряди накопичуються і дерево може бути джерелом напруги.

“Громовідвід”

Обчислити висоту громовідводу та площу, яку він захищає, якщо радіус “захищеного” круга 50 м, а кут між громовідводом і твірною конуса безпеки 60 0Розв’язання:

h= 50м : tg 60°= 29,4м

S= 3.14 *2500 = 7850м2= 78,5а

Відповідь: 29,4м; 78,5а

Задача 3

Скільки потрібно оленячих шкур, площею 3,8 м2, для покриття чума (переносне житло у вигляді конуса), якщо діаметр основи 16м, а основна жердина √20м.

Розв’язання

R = 16:2 = 8

L2= √202 + 82 =84, L = 2√21м

S = 3,14*8*2√21= 230,23м2

230,23: 3,8 = 60,6 ≈61(штук)

Відповідь:61 штук.

Задача 4

Нехай довжина основи конічної купи щебеню 12м. Довжина двох твірних 4,6 м. Знайти площу поверхні купи щебеню.

Розв’язування:

L = 4,6/2 = 2,3 м

R = 12,1 /6,28 1,9 м

S = π · R · L = 3,14 * 1,9*2,3 = 13,7(м2)

Відповідь: 13,7 м2

Задача 5

Верхня частина башні має форму конуса, радіус основи якого 11/πм, а твірна 9м..Бічну поверхню планують покрити мозаїкою. Скільки мішків клею потрібно купити для виконання цієї роботи, якщо витрати клею 5 кг на 1м2, а в одному мішку 25 кг

Розв’язання

S=πRL

S = π*11/π*9= 99м2

25:5 = 5м2 99: 5 = 19,8 ( мішків)

Відповідь: 20 мішків.

Задача 6

 Конусоподібний намет  висотою 4,5 м і діаметром основи 6 м покрито тканиною. Скільки тканини пішло на намет?

Розв’язання

 Для того, щоб знайти кількість тканини, яку витратили на намет, необхідно знайти бічну поверхню конуса. Бічна поверхня конуса обчислюється за формулою: S= π RL. Знайдемо радіус основи: ОК=3 (м).  Твірну конуса l = MK знайдемо з прямокутного ∆MОK (∠О = 90Твірну конуса l = MK знайдемо з прямокутного ∆MОK (∠О = 90 ) за теоремою Піфагора. Знайдемо бічну поверхню конуса: (м 2 ).

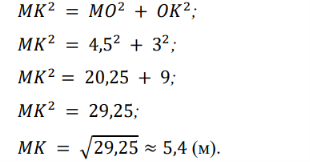
S=3.14*3*3.5=50,9 (м20

Відповідь: 50,9 м2

Задача 7.

Ліхтар закріплений на висоті 8 м. Кут розсіювання ліхтаря 120 градусів.Визначити, яку поверхню освітлює ліхтар.

Розв’язування.

Освітлювальна поверхня кола- основа конуса.Лампа ліхтаря-його вершина. Промені, які напрямлені на коло основи- твірні конуса. В осьовому перерізіконуса- рівнобедрений трикутник в я кому проведено висоту, тоді кути в прямокутному трикутнику 30 та60 градусів.З цього слідує, що твірна дорівнює 16 см. Радіус  основи за теоремою Піфагора: (см)

Площа освітленох поверхні:

Π*1.92=603 м кв

Відповідь:  603 м кв

Задача 8.

Обчислити скільки метрів герлянди  знадобиться для прткрашення ялинки Герлянда буде висіти під кутом 30 градусів при вершині Висота ялинки-12 м довжина вітки ялинки при основі-5 м.

Розв’язування.

Форму ялинки розглянемо, як конуссссс з висотою 12 м та радіусом 5 м. Нитки герлянд, закріплені на вершині ялинки по бічній поверхні під кутом 60 градусів. 360/30=12 (ниток)-герлянд на ялинці.Довжина нитки це цого твірна.В осьовому перерізі конуса- рівнобедрений трикутник.Розглянемо прямокутний трикутний , в якому твірна дорівнює 12м.Тоді довжмна всієї герлянди 12*13=156(м).

Відповідь: 156м.