Прикладні задачі з планіметрії

ПРИКЛАДНІ ЗАДАЧІ З ПЛАНІМЕТРІЇ

 

Вивчення математики, зокрема геометрії, традиційно здійснюється через розв’язування задач, і прикладних задач особливо. При цьому бажано:

• щоб задача демонструвала практичне застосування математичних ідей і методів;
• ілюструвала матеріал, що вивчається на уроці;
• містила відомі або інтуїтивно зрозумілі учням поняття та терміни, а також реальні числові дані, що не ведуть до громіздких обчислень.

За таких умов використання прикладної задачі, складеної на матеріалах суміжних предметів, може дати потрібний педагогічний ефект і необхідні практичні знання.

Я пропоную добірку задач практичного змісту для 7 – 9 класів.

Дана добірка задач може слугувати для педагогів допоміжним дидактичним матеріалом при проведенні уроків математики. А саме: для роботи з учнями, що виявляють цікавість до математики, при підготовці до занять шкільного математичного гуртка, математичної олімпіади, допомагати учням при підготовці до міжнародного конкурсу «Кенгуру».

Розв’язуючи прикладні задачі, діти мають можливість підвищити рівень якості знань, розширити кругозір в області математики. Також даний матеріал сприяє творчій самоосвіті школярів, розвитку пізнавальної активності.

В своїй практиці задачі з добірки я використовую на уроках геометрії, демонструючи міжпредметні зв’язки та зв'язок математики з реальною дійсністю.

 

Задачі для 7 класу

Ознайомлення школярів з прикладними задачами слід розпочинати вже з 7 класу. Тому пропоную для 7 класу добірку таких задач.

Задача 7.1. На сільській дорозі, яка є прямою, послідовно стоять чотири хати на відстані 100м одна від одної. У якій точці дороги треба викопати колодязь, щоб сума відстаней від нього до всіх хат була найменшою.

Задача 7.2. У деякому царстві 6 міст з’єднали прямими шляхами, які не перетиналися так, щоб між будь-якими двома містами був прямий як стріла шлях. Цей шлях може проходити через інше місто (або міста). Соловей-розбійник грабує тільки на Великих дорогах, тобто на таких прямих шляхах, де містяться всі міста царства, за винятком одного-двох. Покажіть, що в деякому царстві можна розмістити міста так, що Великих доріг не буде.

Задача 7.3. Який кут утворюють годинна і хвилинна стрілки годинника, коли вони показують: 1) 6год; 2) 3год; 3) 4год?

Задача 7.4. Скільки разів на добу стрілки годинника утворюють: 1) розгорнутий кут; 2) прямий кут?

Задача 7.5. Відстань між Сумами та Житомиром дорівнює 480км. Житомир розташований на відстані 140км від Києва. Визначте відстань від Києва до Сум, вважаючи, що всі три міста розташовані на одній прямій.

Розв’язування.

Математична модель: знайти довжину відрізка, якщо відомі довжини відрізків, з яких він складається.

Позначимо відстань між Сумами та Житомиром СЖ = 480км, а відстань між Житомиром та Києвом  ЖК = 140км (рис. 1.)

Рис. 1.

Отже, потрібно знайти довжину відрізка СК:

СК = СЖ + ЖК

СК = 480 + 140,

СК = 620

Тобто відстань від Києва до Сум дорівнює 620км.

Відповідь: 620км.

Задача 7.6. Північний вітер змінився на північно-східний. Який кут повороту вітру?

 

Задачі для 8 класу

Для 8 класу можна запропонувати такий підбір прикладних задач.

Задача 8.1. Довжина кімнати 5,4м, а ширина 4,2м. В кімнаті два вікна шириною 1,2м і висотою 1,6м. Освітленість кімнати вважається нормальною, якщо площа (світлова площа) вікон складає 20% від площі підлоги. Чи нормальна освітленість кімнати?

Задача 8.2. На більярдному столі прямокутної форми лежить дві кульки. Вкажіть декілька направлень ударів, при яких перша кулька попадає в другу (розташування кульок оберіть самостійно).

Задача 8.3. Задача Бхаскари. Квітка лотоса при вертикальному положенні стебла піднімалась над водою на фута. Вітер відхилив її на 2 фути від попереднього положення (по поверхні води). Після цього квітка лотоса опинилася на рівні води. Визначте глибину озера в цьому місці.

Задача 8.4. Задача Л.Пізанського (ХІІ – ХІІІ). Дві вежі, одна з яких заввишки 40 футів, а друга – 30 футів, розташовані на відстані 50 футів одна від одної. До криниці, що була між ними, одночасно з кожної вежі злетіла пташка. Рухаючись з однаковою швидкістю, вони прилетіли до криниці одночасно. Знайдіть відстань від криниці до найближчої вежі (у футах).

Задача 8.5. Задача ал-Каші. Спис стояв у воді вертикально і піднімався над водою на 3 лікті. Вітер відхилив його так, що вершина списа зрівнялась з поверхнею води на відстані 5 ліктів від початкового положення списа. Знайти довжину списа.

Задача 8.6. 25 горіхів розклали у вигляді квадрата. Покажіть, що їх можна розмістити у вигляді таких двох рівносторонніх трикутників, що сторона одного із них дорівнює стороні квадрата, а другого – на одиницю менша.

Задача 8.7. Одна допитлива мураха зацікавилася геометрією. Вона повзе по ламаній, всі ланки якої рівні, повертає лише за годинниковою стрілкою і завжди на один і той же кут. При яких кутах повороту вона повернеться в початкову точку?

Задача 8.8. Бетонна плита з прямолінійними сторонами повинна мати форму прямокутника. Як за допомогою мотузки перевірити правильність форми плити?

Задача 8.9 До горизонтальної балки на двох однакових нитках підвішено вантаж масою Р (рис. 2.). Визначте силу натягу ниток.

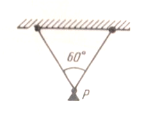
Рис. 2.

Задача 8.10. З якою силою F треба утримувати вантаж масою Р на похилій площині, щоб він не скочувався вниз?

Задача 8.11. Чи можна з круглого листа заліза діаметром 1,4м вирізати квадрат із стороною 1м?

Задача 8.12. Чи можуть побачити один одного космонавти, які летять над поверхнею Землі на висоті 230км, якщо відстань між ними по прямій дорівнює 2200км? Радіус Землі 6370км.

Задача 8.13. Між двома фабричними будівлями побудовано похилий жолоб для транспортування металів. Відстань між будівлями дорівнює 10м, а кінці жолоба розташовані на висоті 8м і 4м над землею. Знайдіть довжину жолоба.

Задача 8.14. На прямолінійному шосе треба знайти місце для автобусної зупинки так, щоб сума відстаней від неї до населених пунктів А і В була найменшою. Розгляньте два випадки: а) населені пункти розміщені з різних боків від шосе (рис. 3.а)); б) населені пункти розміщені з одного боку від шосе (рис. 3.б)).

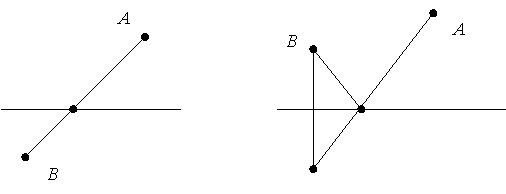
а                                                                              б

Рис. 3.

Задача 8.15. Тінь від вертикальної жердини, висота якої дорівнює 7м, становить 4м (рис. 4.). Виразіть у градусах висоту сонця над горизонтом.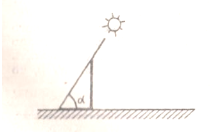
 

Рис. 4.

Задача 8.16. „Стрибок мавпи”. На дереві сиділи дві мавпочки: одна – на самій верхівці дерева, інша – на висоті 10 ліктів від землі. Другій мавпочці захотілося напитися води з джерела, що знаходиться на відстані 40 ліктів від дерева. Вона злізла з дерева і пострибала до води. У той самий час перша зістрибнула з дерева і потрапила до того ж джерела. Обидві мавпочки подолали однакову відстань. Скажи, о мудра людина, з якої висоти стрибнула друга мавпочка?

Задача 8.17. „Зламаний бамбук”. Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о юний математик, на якій відстані від землі було зламано бамбук?

Задача 8.18. Висоти двох вертикальних стовпів дорівнюють 5м та 12,5м. Відстань між ними 10м. Знайти найменшу довжину троса, яким можна з’єднати верхні кінці стовпів.

 

Задачі для 9 класу

Для 9 класу пропоную підбір задач з окремих тем.

 

Площа круга та його частин

Задача 9.1. Дерево має 1,884м в обхваті. Чому дорівнює площа перерізу, що має приблизно форму кола?

Задача 9.2. Вода тече по двох трубах із однаковою швидкістю. Перша труба має діаметр 20см, а друга – 15см. У скільки разів подача води з другої труби менша ніж з першої?

Задача 9.3. Круглу клумбу, радіус якої 6м, розділили на дві рівні частини колом, центр якого збігається з центром клумби. Чому дорівнює радіус цього кола?

Задача 9.4. Дві труби, внутрішні діаметри яких дорівнюють 15мм і 25мм, потрібно замінити однією, не змінюючи їхньої пропускної здатності. Яким має бути внутрішній діаметр нової труби?

Задача 9.5. Два прожектори розміщені один напроти іншого на прямолінійних паралельних протилежних берегах ріки. Відстань між прожекторами дорівнює 12км. Прожектори можуть освітлювати місцевість радіусом 10км кожний. Чому дорівнює площа поверхні ріки, освітлюваної цими прожекторами?

Задача 9.6. Коза прив’язана до кілка мотузкою, довжина якої 10м. Знайти площу ділянки, на якій вона може пастися.

Задача 9.7. Верблюд пробіг два кола по арені цирку, радіус якої 5м. Яку відстань пробіг верблюд?

Задача 9.8. Щоб зробити викройку спідниці „сонце” для дівчинки, побудували два концентричні кола, довжина одного з цих кіл дорівнює довжині „обхвату талії” 62,8см, а радіус другого кола більший радіусу першого на 60см (довжину спідниці). Скільки квадратних метрів тканини потрібно на пошиття спідниці?

Задача 9.9. На будинку встановлено годинник із круговим циферблатом, що має діаметр 8,8м. Знайти площу циферблата цього годинника та порівняти її з площею класної кімнати.

 

Подібність фігур

Задача 9.10. Тінь, що відкидається стовпом на поверхню землі, дорівнює 9м, у той самий час стрижень висотою 2м відкидає тінь 2,4м. Знайти висоту стовпа.

Задача 9.11. Стовп висотою 15м закривається монетою діаметром 2см, якщо тримати її на відстані 70см від ока. Знайти відстань від стовпа до спостерігача.

Задача 9.12. Як знайти висоту предмета, до основи якого можна підійти?

Задача 9.13. Як знайти висоту предмета, до основи якого не можна підійти?

Задача 9.14. На рисунку 5 зображено план садиби у масштабі 1:1000. Визначте розміри садиби (довжину і ширину).

Рис. 5.

Задача 9.15. Довжина тіні фабричної труби дорівнює 35,8м. У той самий час вертикально поставлена жердина завдовжки 1,9м дає тінь довжиною 1,62м (рис. 6.). Знайдіть висоту труби.

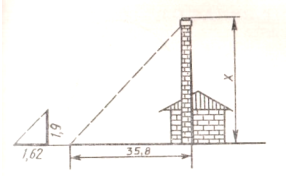
Рис. 6.

Задача 9.16. Як далеко видно з літака, який летить на висоті 4км над Землею, якщо радіус Землі 6370км?

Задача 9.17. Обчисліть радіус горизонту, що видно з вершини телебашти в Останкіно, висота якої 537м.

 

Теореми косинусів і синусів

Задача 9.18. Два пароплави починають свій рух одночасно з одного порту та рухаються рівномірно по прямих, що перетинаються під кутом φ. Швидкість першого пароплава – а км/год, іншого – b км/год. Обчислити, на якій відстані будуть знаходитися пароплави через х годин.

Задача 9.19. О 7 год. ранку пасажирський літак вилетів з міста А. Після півгодинної зупинки в місті В о 8 год. 10 хв. літак зробив поворот на 35° вправо та о 9 год. здійснив посадку в місті С. Знайти відстань між містами А та С, якщо середня швидкість літака на кожній ділянці польоту дорівнювала 320 км/год.

Задача 9.20. Залізний стрижень довжиною а потрібно зігнути під прямим кутом так, щоб відстань між кінцями дорівнювала А. Де має знаходитися точка згину? За яких умов задача має розв’язок? Розглянути цю задачу за умови, що кут згину дорівнює 60°, 120°.

Задача 9.21. Зі спостережного пункту помічають під кутом 63,5° літак, що пролітає над вежею, висота якої 79,5м. Пряма, що сполучає спостережний пункт із верхівкою вежі, утворює з горизонтальною площиною кут 20°45'. На якій висоті знаходиться літак?

Задача 9.22. З вертольота, що знаходиться над шосейною дорогою, було помічено колону машин, яка рухається по ній. Початок колони видно під кутом 75°, а кінець – під кутом 70°. Знайти довжину колони, якщо вертоліт знаходиться на висоті 1650м.

Задача 9.23. Дорога вгору піднімається двома уступами у вигляді ламаної лінії. Перший уступ утворює з горизонтом кут 30°, другий – 65°, а пряма, що сполучає вершину гори з її основою, нахилена до горизонту під кутом 60°. Довжина першого уступу дорівнює 1км. Знайти висоту гори.

Задача 9.24. Судно йде на схід зі швидкістю 12 вузлів. О 13 год. 10 хв. азимут напрямку на маяк дорівнював 70°, а о 13 год. 40 хв. – 20°. На якій відстані від судна знаходиться маяк о 13 год.? (1 вузол відповідає 1 морській милі за годину.)

Задача 9.25. У стіні шахти на однаковій висоті пробито два штреки, входи у які віддалені один від одного на 4м. Перший штрек має довжину 350м і спрямований перпендикулярно до стіни. Довжина другого штреку дорівнює 420м, і він спрямований під кутом 125° до стіни шахти. Кінці цих штреків сполучено третім штреком. Яка довжина третього штреку? У якому напрямку треба розмістити штрек від кінців даних штреків, якщо роботу треба починати з обох кінців одночасно?

Задача 9.26. Спостерігач знаходиться на відстані 50м від вежі, висоту якої він хоче виміряти. Основу вежі він бачить під кутом 10° до горизонту, а вершину – під кутом 45° до горизонту. Яка висота вежі?

Задача 9.27. На горі стоїть вежа висотою 100м. Біля підніжжя гори знаходиться одна людина. Інша спостерігає її спочатку з вершини вежі під кутом 60° до горизонту, а потім з її основи під кутом 30°. Знайти висоту гори.

 

 

Правильні многокутники

Задача 9.28. Села А та В знаходяться на однаковій відстані від міста М. На прямій, що проходить через М і В, розміщені ще два села С та D. До якого із сіл (А чи В) ближче розміщено село С, село D?

Задача 9.29. Чотири будинки розміщені у вершинах земельної ділянки, що має форму опуклого чотирикутника. Де на цій ділянці потрібно викопати колодязь, щоб сума всіх відстаней від кожного будинку до колодязя була найменшою?

Задача 9.30. Кути квадратного залізного листа зі стороною а зрізали так, що отримали правильний восьмикутник. Знайти його сторону.

Задача 9.31. На колі потрібно розмістити центри отворів для 15 болтів так щоб відстань між центрами отворів була 30мм. Якої довжини має бути радіус кола?

Задача 9.32. Як скласти паркет із правильних восьмикутників і квадратів; із дванадцятикутників і трикутників?

Задача 9.33. Чи можна скласти паркет із правильних десятикутників і п’ятикутників?

Задача 9.34. З яких правильних многокутників одного виду можна скласти паркет?

Задача 9.35. Кінець валика діаметром 4см обпиляне у вигляді квадрата. Визначте, який найбільший розмір може мати сторона квадрата.

Задача 9.36. Знайдіть радіус земної кулі, виходячи з того, що 1м становить одну 40-мільйонну частку довжини екватора.

Задача 9.37. На скільки б подовшав земний екватор, якби радіус земної кулі збільшився на 1см?

Задача 9.38. Шків має у діаметрі 1,4м і робить 80 обертів за хвилину. Знайдіть швидкість точки на ободі шківа.

Задача 9.39. Який кут утворюють радіуси Землі, проведені до двох точок на її поверхні, відстань між якими дорівнює 1км? Радіус Землі дорівнює 6370км.

 

Довжина кола

Задача 9.40. Ведуче колесо паровоза робить 6 об/с, діаметр колеса 120см. Знайти швидкість паровоза.

Задача 9.41. Піднімаючи воду з колодязя, вал робить 18 обертів. Обчислити глибину колодязя, якщо діаметр вала 20см.

Задача 9.42. Довжина хвилинної стрілки на Спаській вежі Московського Кремля 3м 27см. Який шлях пробігає її кінець за 1 хв.? за 1 годину?

Задача 9.43. З жерсті зробили одну трубу діаметром 18см і три однакові труби тієї самої довжини. Обчислити радіус менших труб.

Задача 9.44. Як обчислити радіус планети, якщо широти пунктів А та В, у яких зроблено вимірювання, дорівнюють відповідно φ і ω, а довжина дуги меридіана між ними дорівнює s?

Задача 9.45. Діаметри коліс трактора дорівнюють 75 і 90см. Який шлях пройде трактор, якщо на цьому шляху переднє колесо зробить на 230 обертів більше, ніж заднє?

Задача 9.46. Довжина орбіти автоматичної космічної станції „Салют” дорівнює 41500км. Вважаючи орбіту круговою, знайти висоту станції над Землею, якщо радіус Землі 6370км.

Задача 9.47. Припустимо, що земну кулю та футбольний м’яч обтягнуто по екватору обручами. Якщо в обох випадках збільшити довжину обручів на 1м і розмістити знову обручі на однаковій відстані від поверхні об’єктів, то утворяться зазори. У якому випадку зазор більший?

Задача 9.48. За два обороти по круговій орбіті навколо Землі космічний корабель пролетів 84152км. На якій висоті над поверхнею Землі знаходиться корабель, якщо радіус Землі дорівнює 6370км?

Задача 9.49. Знайти довжину маятника стінного годинника, якщо кут його коливання становить 38°, а довжина дуги, що описує кінець маятника, дорівнює 24см.

Задача 9.50. Тепловоз пройшов 1413м. Знайти діаметр колеса, якщо воно зробило 300 обертів.

Задача 9.51.Радіус заокруглення шляху залізничного полотна дорівнює 5км, а довжина дуги заокруглення – 400м. Яка градусна міра дуги заокруглення?

Задача 9.52. Скільки спиць у колесі, якщо кожний з кутів, розміщених між двома сусідніми спицями, дорівнює 18^o ?

Задача 9.53. Зубчасте колесо з 60 зубцями зчеплене з іншим, що має 75 зубців. На який кут повернеться друге колесо при одному повному оберті першого?

Задача 9.54. Діаметри двох зчеплених зубчастих коліс відносяться як 3 : 8. На який кут повернеться більше колесо при одному повороті меншого?

Задача 9.55. На який кут повернеться Земля навколо своєї осі за 8 год.? На який кут за цей час повернеться годинна стрілка?

Задача 9.56. Як змінюється кут між годинною і хвилинною стрілками впродовж 1хв; 12хв; 46хв?

 

Площі многокутників

Задача 9.57.Основа постаменту пам’ятника має форму квадрата зі стороною 6м. Навколо пам’ятника розміщена клумба шириною 2м. Знайти площу клумби.

Задача 9.58. Освітлення кімнати вважається нормальним, якщо площа прорізів вікон не менша за 0,2 площі підлоги. Визначити, чи нормально освітлена ваша класна кімната.

Задача 9.59. Необхідно відштукатурити стіну довжиною 8,25м і висотою 4,32м, що має три вікна розміром 2,2м 1,2м кожне. Знайти площу поверхні стіни, яку необхідно відштукатурити.

Задача 9.60. Сад має форму прямокутника зі сторонами 580м і 376м. Скільки в ньому яблунь, якщо на кожну яблуню припадає в середньому 16м²? Який виторг дав сад після продажу яблук, якщо з 1га зібрано по 35т яблук і кожна тонна продана в середньому по 2,5грн?

Задача 9.61. Підлогу кімнати, що має прямокутну форму розміром 11м 8,8м, потрібно вистелити паркетом, одна плитка якого має розмір 5см 25см. Скільки потрібно плиток паркету, якщо на припасування і прирізку витрачається 3 % від загальної площі?

Задача 9.62. Кожну із двох рівновеликих ділянок потрібно обнести огорожею. Одна ділянка має форму квадрата зі стороною 80м, а інша – форму прямокутника, одна сторона якого дорівнює 50м. На яку огорожу буде потрібно більше матеріалу і на скільки, якщо на кожні 12м потрібно 1м³ пиломатеріалів?

Задача 9.63. Трактор, рухаючись зі швидкістю 15км/год, тягне за собою дискову сівалку з робочою шириною захвату 6м. Скільки гектарів можна засіяти у такий спосіб за 8-годинний робочий день?

Задача 9.64. До будинку необхідно зробити добудову з трьох стін, використовуючи одну зі стін будинку. Виявилося, що цегли вистачить на 100м стіни (по периметру трьох нових стін). Добудова має бути максимальною за площею. Які розміри добудови вибрати?

Задача 9.65. Прямокутна квіткова клумба займає площу 216м². Уздовж довгих сторін необхідно прокласти доріжки шириною 2м, уздовж коротких – шириною 3м. Які мають бути розміри прямокутної ділянки (клумби разом з доріжкою), щоб площа доріжок була найменшою?

Задача 9.66. Один новосел вирішив вистелити різнобарвними квадратними плитками підлогу в кухні площею 7,29м² і купив такий набір: 1 плитка зі стороною 120см, 3 плитки зі стороною 90см, 9 плиток із стороною 60см і 2 плитки зі стороною 30см. Інший новосел для такої самої підлоги купив 2 плитки зі стороною 120см, 2 плитки зі стороною 90см, 8 плиток зі стороною 60см і 2 плитки зі стороною 30см. Хто з них вигадав?

Задача 9.67. Ділянку, що має форму прямокутника, потрібно розділити двома межами, що виходять з одного кута, на три рівновеликі частини. Як це зробити?

Задача 9.68. Ділянку, що має форму прямокутника, потрібно розділити трьома межами на чотири рівновеликі частини. Як це зробити?

Задача 9.69. Поверхня озера має форму квадрата. У вершинах квадрата на березі озера ростуть чотири дуби. Треба удвічі збільшити площу поверхні озера так, щоб нове озеро зберегло форму квадрата і щоб усі чотири дуби залишилися на своїх місцях. Як це зробити?

Задача 9.70. Потрібно вистелити підлогу кімнати розміром 6м 4м плитками правильної шестикутної форми. Скільки таких плиток необхідно мати, якщо сторона плитки 20см?

Задача 9.71. Підлогу прямокутного фойє театру, розміри якого 4,6м 8,4м, потрібно покрити керамічною плиткою двох різних кольорів (порівну кожного кольору). Скільки потрібно плиток кожного кольору, якщо плитка має форму правильного шестикутника зі стороною 10см?

Задача 9.72. Сторони двох земельних ділянок квадратної форми дорівнюють 100м та 150м. Знайдіть сторону рівновеликої їм квадратної ділянки.

Задача 9.73. На плані, виконаному в масштабі 1 : 200, місце для установки деякого об’єкта займає 360см². Яку площу воно займає насправді?

 

 

Використані джерела

1.     Бевз Г.П. Геометрія 7 / Григорій Петрович Бевз, Валентина Григорівна Бевз, Наталія Григорівна Владімірова – Тернопіль: Підручники і посібники, 2006. – 208 с.
2.     Бурда М.І. Геометрія 7 / Михайло Іванович Бурда, Ніна Анатоліївна Тарасенкова. – К.: Зодіак – ЕКО, 2007. – 208 с.
3.     Бурда М.І. Геометрія 8 / Михайло Іванович Бурда, Ніна Анатоліївна Тарасенкова. – К.: Зодіак – ЕКО, 2008. – 240 с.
4.     Варданян С.С. Задачи по планиметрии с практическим содержанием / С.С. Варданян. – М.: Просвещение, 1989. – 258 с.
5.     Гуменюк О.В. Спробуй розв'яжи!: Цікаві математичні задачі / О.В. Гуменюк. – К.: ВЦ «Академія», 1998. – С. 58.
6.     Игнатьев В.А. Сборник математических задач повышенной трудности / В.А. Игнатьев, Я.А. Шор. – М.: Просвещение, 1990. – 57 с.
7.     Александров А.Д. Геометрия, 7-11. / Александр Данилович Александров, Алексей Леонидович Вернер – М.: Просвещение, 1991. – 312 с.
8.     Апостолова Г.В. Геометрія, 7-11 / Галина Вадимівна Апостолова. – К.: Поліграф сервіс, 2001. – 205 с.
9.     Погорєлов О.В. Геометрія: підручник для 7-11 кл. серед. шк. – 3-е вид. / Погорєлов Олексій Васильович. – К.: Освіта, 1993. – 384 с.