Презентація " Вектори на площині"
Про матеріал
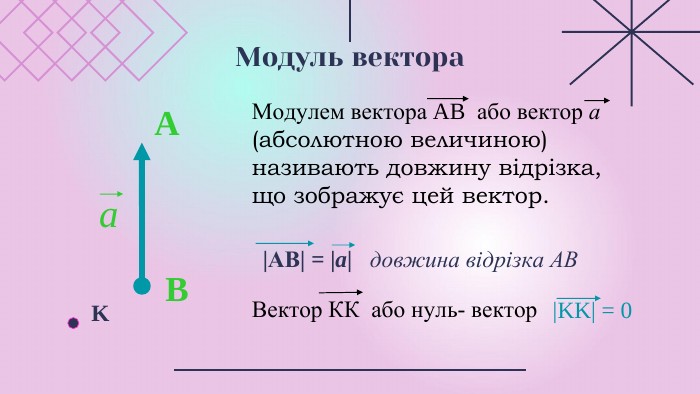
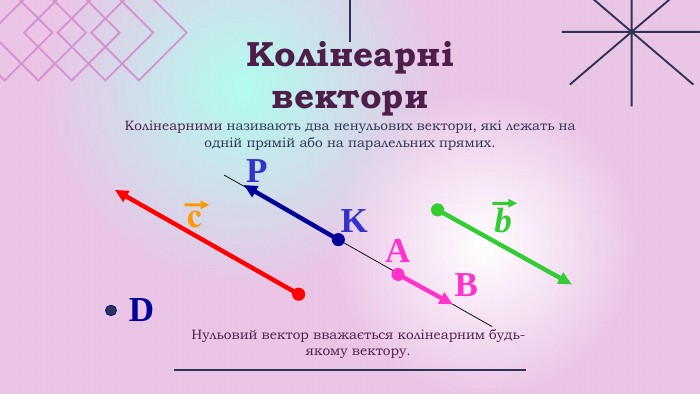
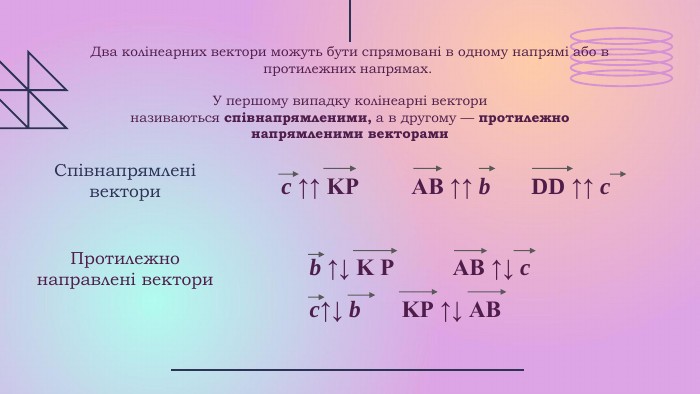
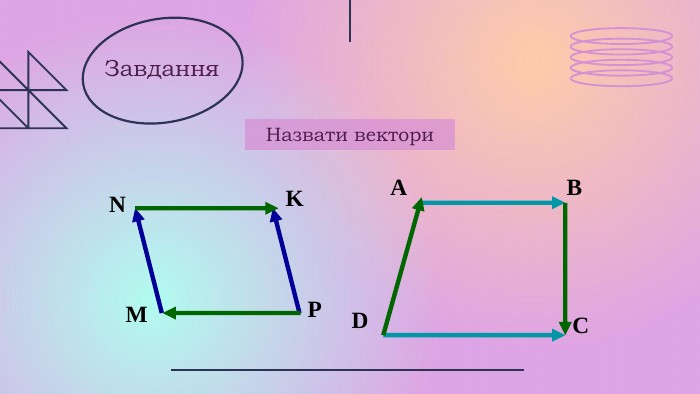
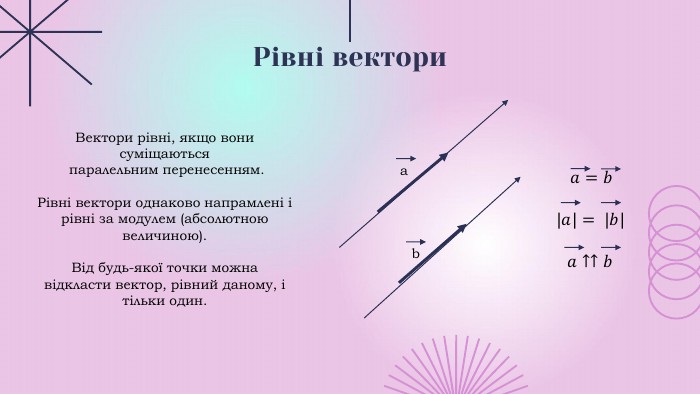
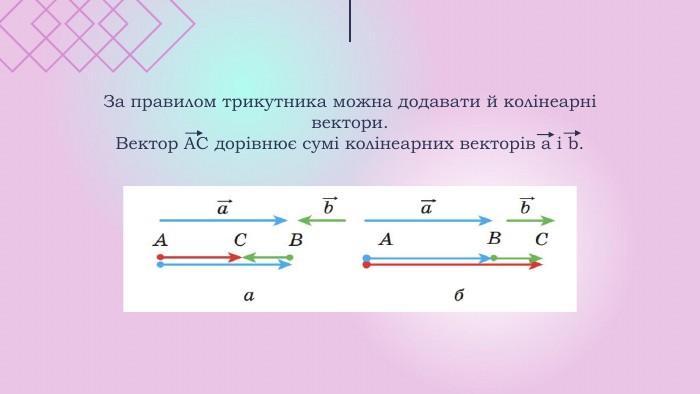
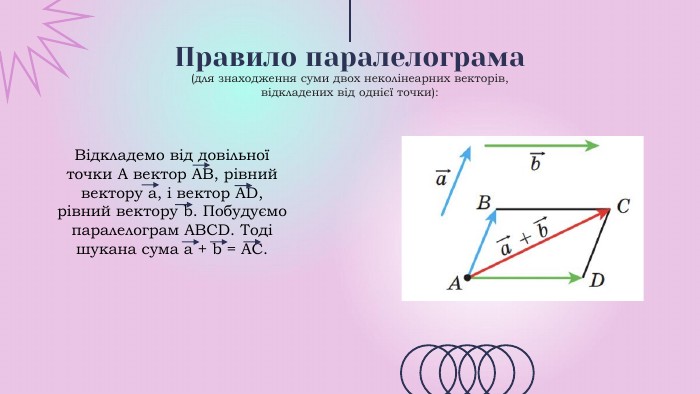
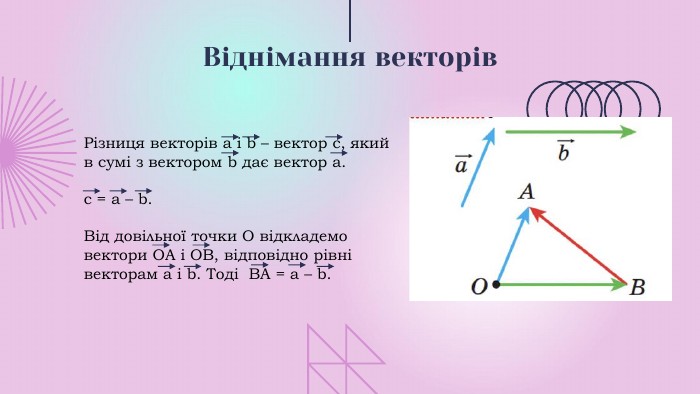
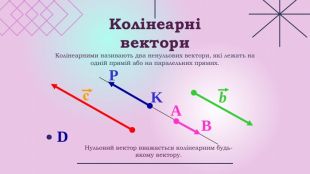
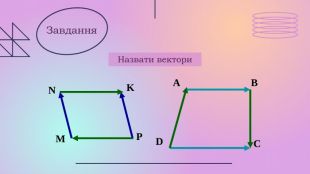
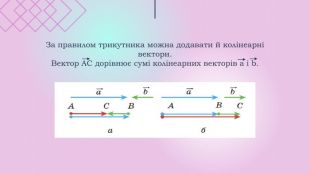
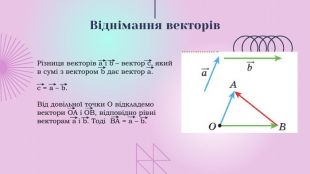
Презентації розкриває сутність теми " Вектори на площині", містить теоретичний та практичний матеріал ( означення, властивості, формули, завдання, рисунки).
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку