Метод інтервалів.

Розв'язування раціональних  нерівностей  методом інтервалів.

Презентація створена учителем математики

Матвійчук Тетяною Володимирівною

■ І. Перед ознайомленням із новим матеріалом пригадайте теоретичний матеріал:

■ 1.Розвязування лінійних нерівностей.

■ 2. Які перетворення не порушують рівносильність нерівності?

■ 3. Що є розв’язком нерівності?

■ 4.Графічна ілюстрація розв’язків нерівностей.

■ 5. Квадратна нерівність та способи її розв’язання.

■ 6.Функція. Її властивості. Область визначення функції . Нулі функції.  Проміжки знакосталості функції. (повторити §2 п.3 ст. 28-29.

Рис 3.1).

■ 7. Розкладання квадратного тричлена на лінійні множники.

ІІ. Ознайомлення із новим матеріалом

Нерівності виду

𝒙 − 𝒂𝒙 − 𝒃𝒙 − 𝒄 … 𝒙 − 𝒌 >, <, ≥, ≤ 𝟎 або

розв’язуються методом інтервалів

Алгоритм розв’язування нерівностей методом інтервалів

1).  Знайдіть D ( f )   функції 𝒚 =𝒇 𝒙 .

2). Знайдіть нулі функції (прирівняйте до нуля кожну дужку).

3). На числову пряму (на область визначення 𝒚 =𝒇 𝒙 ) в порядку зростання розташуйте нулі функції.

4). Нулі  функції розбивають область визначення функції 𝒚 =𝒇 𝒙 на проміжки знакосталості, крайній правий з яких завжди додатний і далі іде чергування знаків, якщо функція 𝒚 =𝒇 𝒙 є неперервною та відсутні особливі випадки.

5). Запишіть розв'язки нерівності.

ОСОБЛИВІ ВИПАДКИ

(ЗАУВАЖЕННЯ)

1). Коефіцієнт біля змінної повинен бути додатним.

2). Відсутні однакові лінійні множники.

3). Відсутні нелінійні множники, які далі не розкладаються.

4). Множники у парній кратності на знак нерівності не впливають.

Приклади розв'язання  нерівностей

1).

Нулі функції:

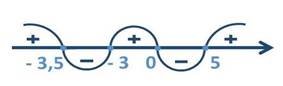Запишемо відповідь, використовуючи числову пряму. Так як  - знак нестрогої нерівності, то дужки будуть квадратні. До відповіді візьмемо проміжки зі знаком «+».

Відповідь: .

2).

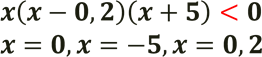Оскільки у першій дужці коефіцієнт біля  від’ємний, помножимо  ліву і праву частину нерівності на (-1), при цьому змінимо знак нерівності. Отримаємо рівносильну нерівність: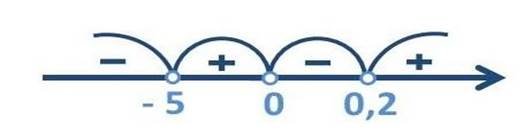    

До відповіді візьмемо проміжки зі знаком «-».

Дана нерівність строга, тому дужки будуть круглі.

Bідповідь:  .

3) 

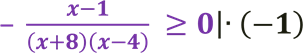
Перед  дробом знак «-» приберемо, помноживши обидві частини нерівності  на (-1). Отримаємо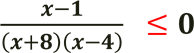

 – нулі функції.

Областю визначення функції 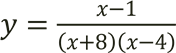 є всі дійсні числа

крім -8 і 4, тому ці

числа на числовій прямій зображаємо у вигляді світлих кружочків.

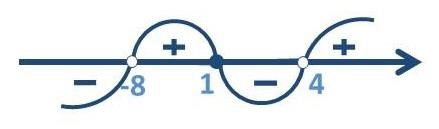                                             Відповідь: .

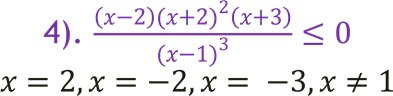
Нуль функції – 2 до нерівності входить у другому (парному) степені, тому при переході через нього функція не змінює знак.

Це не стосується нуля функції 1, який не належить  області визначення. Оскільки 1 корінь непарної кратності.

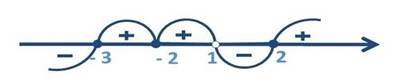
Зверніть увагу, що при , ліва частина нерівності перетворюється у нуль, що задовольняє умову нерівності, тому до розв’язків включено число -2.

Відповідь:

5).

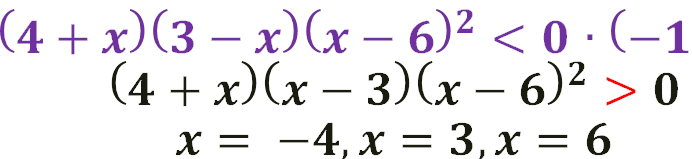
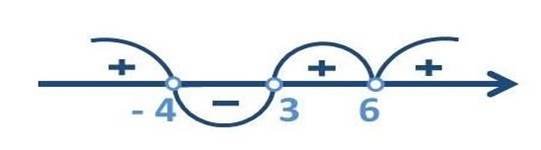
Відповідь: 

1.Опрацюйте §2 п.310 ст.112 – 115. Особливу увагу зверніть на розв’язання Прикладів 1, 2 та 3.

2.Розв'яжіть самостійно: № 10.1 (3, 5), 10.3 (3, 4), 10.7 ( 3, 4).

ДЯКУЮ ЗА УВАГУ!  БАЖАЮ УСПІХІВ!