Проблемне навчання на прикладі уроків математики

МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИУКРАЇНСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ ІМЕНІ М. П. ДРАГОМАНОВАФАКУЛЬТЕТ МАТЕМАТИКИ, ІНФОРМАТИКИ ТА ФІЗИКИЗаочне відділення. Робота З ДИСЦИПЛІНИ «Комп”ютерно-орієнтовані системи навчання математики» На ТЕМУ «Проблемне навчання на прикладі уроків математики»Виконала:студентка 1 курсу групи 1ммз. СО Мігульова Ольга Віталіївна

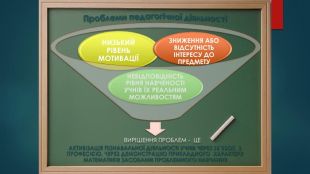
НИЗЬКИЙ РІВЕНЬ МОТИВАЦІЇНЕВІДПОВІДНІСТЬ РІВНЯ НАВЧЕНОСТІ УЧНІВ ЇХ РЕАЛЬНИМ МОЖЛИВОСТЯМЗНИЖЕННЯ АБО ВІДСУТНІСТЬ ІНТЕРЕСУ ДО ПРЕДМЕТУВИРІШЕННЯ ПРОБЛЕМ - ЦЕАКТИВІЗАЦІЯ ПІЗНАВАЛЬНОЇ ДІЯЛЬНОСТІ УЧНІВ ЧЕРЕЗ ЗВ’ЯЗОК З ПРОФЕСІЄЮ, ЧЕРЕЗ ДЕМОНСТРАЦІЮ ПРИКЛАДНОГО ХАРАКТЕРУ МАТЕМАТИКИ ЗАСОБАМИ ПРОБЛЕМНОГО НАВЧАННЯПроблеми педагогічної діяльності

порівняльна характеристика традиційного і проблемного навчання {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Традиційне навчання. Проблемне навчання. Навчальний матеріал подається у готовому вигляді. Педагог основну увагу звертає на програму навчання, дотримання її вимог, оцінювання учнів. Новий навчальний матеріал учні отримують під час вирішення теоретичних і практичних проблем, в процесі пошукової, дослідницької, самостійної діяльності. Під час учіння виникають певні прогалини, перепони й труднощі, викликані тимчасовим вилученням учня з процесу навчання. Контроль навчальних досягнень тільки частково пов’язаний з процесом навчання: він не єскладовою цього процесу. Під час вирішення проблемної ситуації учні навчаються самостійно долати труднощі. Підвищена пізнавальна активність учнів сприяє розвитку позитивних мотивів навчальної діяльності, зменшує необхідність формальної перевірки результатів.

порівняльна характеристика традиційного і проблемного навчання {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Темп навчання залежить від навчальної програми. Темп навчання залежить від індивідуально-психічних якостей учнів. Вчитель створює різні дидактичні ситуації, що відповідають особливостям тих, хто вчиться, їх рівню знань та інтелектуальним можливостям. Відсутність можливості досягнення більшістю учнів високих навчальних результатів; найбільше утруднення викликає використання й застосування отриманих знань й інформації на практиці. Результати навчання є достатньо високими та стійкими. Учні з легкістю використовують отримані знання на практиці та водночас розвивають своївміння й здібності.

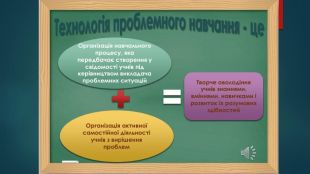
Організація навчального процесу, яка передбачає створення у свідомості учнів під керівництвом викладача проблемних ситуацій. Творче оволодіння учнів знаннями, вміннями, навичками і розвиток їх розумових здібностей. Організація активної самостійної діяльності учнів з вирішення проблем. Технологія проблемного навчання - це

В проблемному навчанні виділяють навчальну проблему, проблемні ситуації, задачу і запитання. Проблемна ситуація  ситуація, для оволодіння якою учень або колектив мають знайти й застосувати нові для себе знання чи способи дій. Вдало створена проблемна ситуація є важливою ланкою наступного засвоєння школярами знань проблемним шляхом, що складається з таких етапів: 1) організація проблемної ситуації (педагог  створює проблемну ситуацію, учень  усвідомлює суперечності у навчальному матеріалі, який вивчається); 2) формулювання проблеми (педагог  організовує обміркування проблеми та її формулювання, учень  формулює навчальну проблему); 3) індивідуальне або групове вирішення проблеми суб'єктами учіння (педагог  організовує вирішення проблеми, формулювання гіпотези, учень  висуває гіпотезу, яка пояснює досліджувану навчальну проблему); 4) верифікація (перевірка, тлумачення і систематизація) отриманої інформації (педагог  організовує перевірку гіпотези, учень  перевіряє гіпотезу шляхом експерименту, вирішення завдань, наукового пошуку тощо); 5) використання засвоєних знань у теоретичній та практичній діяльності (педагог  організовує узагальнення результатів попередніх дій і використання здобутих знань на практиці, учень  аналізує отримані результати. Формулює висновки, використовує їх у практичній діяльності)

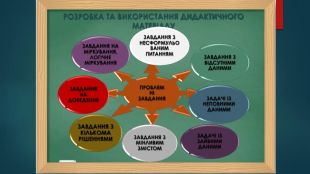
РОЗРОБКА ТА ВИКОРИСТАННЯ ДИДАКТИЧНОГО МАТЕРІАЛУПРОБЛЕМНІ ЗАВДАННЯЗАВДАННЯ З НЕСФОРМУЛЬОВАНИМ ПИТАННЯМЗАВДАННЯ З ВІДСУТНІМИ ДАНИМИЗАДАЧІ ІЗ НЕПОВНИМИ ДАНИМИЗАДАЧІ ІЗ ЗАЙВИМИ ДАНИМИЗАВДАННЯ З МІНЛИВИМ ЗМІСТОМЗАВДАННЯ З КІЛЬКОМА РІШЕННЯМИЗАВДАННЯ НА ДОВЕДЕННЯЗАВДАННЯ НА МІРКУВАННЯ, ЛОГІЧНЕ МІРКУВАННЯr

Приклади проблемних ситуацій, які використовують на уроках математики. Вивчення теми «Площа трикутника» (геометрія 8 клас) Задача. Три маляри повинні пофарбувати фронтон будинку у формі прямокутного трикутника зі сторонами 3 м та 4 м. Чи вистачить їм 1 банки фарби, якщо на ній написано: площа покриття 10 г/м2?

Переведемо задачу на математичну мову. Знайдіть площу S прямокутного трикутника, якщо один із катетів 3 м, а інший – 4 м. Окремі учні здогадалися – знаючи формулу площі прямокутника, зможуть розв’язати це завдання. Перша проблемна ситуація: Як обчислити площу прямокутного трикутника, знаючи формулу для знаходження площі прямокутника? Учні пропонують: добудувати цей трикутник до прямокутника (Якщо прямокутний трикутник добудуємо до прямокутника, то ми отримаємо два рівні трикутники, які рівні за двома катетами). Обчислюють площу прямокутника, а потім знаходять площу прямокутного трикутника.

Друга проблемна ситуація: Чи завжди можемо використовувати формулу, якщо трикутники бувають різної форми?Задача. Найти площу довільного гострокутного трикутника. За допомогою навідних питань учні знаходять спосіб. Вони пропонують добудувати гострокутний трикутник до паралелограма.• Доводимо, що отримані 2 трикутники рівні за 3-ю ознакою рівності трикутників.• Згадуємо формулу площі паралелограма;• Виводимо формулу площі будь-якого гострокутного трикутника;• Відповідаємо на питання задачі: площа будь-якого гострокутного трикутника дорівнює половині твору його основи на висоту.

Третя проблемна ситуація: Знайти площу будь-якого тупокутного трикутника. З цією проблемою учні справляються швидко. Вирішення основної проблеми. Знайти площу довільного трикутника. Проаналізувавши всі випадки, зробіть висновок. Запитання. Чому дорівнює площа довільного трикутника? Передбачувана відповідь учнів. Площа довільного трикутника дорівнює половині добутку його основи на висоту.

Тема «Логарифм числа»Пропонуємо розв’язати рівняння а). 5х = 25 і б). 5х = 10. Учні легко розв’язують рівняння а). х = 2 . А як розв’язати рівняння б), адже немаєтакого показника степеня піднісши до якого число 5 одержимо 10. Розв’язати такерівняння зможемо після вивчення поняття логарифма.

Створення проблемних ситуацій через виконання невеликих дослідницьких завдань. У початку системи координат поставлено коня. Він ходить як шаховий (тільки не в клітинах, а вузлах координатної сітки); зафарбуйте вузли координатної сітки у шаховому порядку. Опишіть, записуючи координати точок, один із маршрутів коня з точки з координатами (0;0) у точку (-1; 1). Придумайте маршрут із 5 ходів, що починається в точці (0; 0) і проходить через точки (4; 0) та (7; 3) із зупинками в цих точках. Чи може кінь колись потрапити у точку (2,5; 3)? Чи може кінь потрапити з точки (0; 0) у точку (2; 2) за 1995 ходів?

У початку координат стоїть слон. Він може ходити як шаховий слон (по вузлах координатної сітки). Опишіть один із найкоротших (за кількістю ходів) маршрут слона з точки (0; 0) у точку (-3, 7). Чому меншої кількості ходів слону не вистачить? Скільки таких найкоротших маршрутів?Опишіть маршрут із чотирьох ходів, що починається у точці (0; 0) і проходить (у будь-якому порядку) через точки (3, -1,5); (11, 5) та (-1;7). Чи можна з точки (0; 0) потрапити слоном у точку (1; 0)?Покажіть, у які точки можна потрапити слоном з початку координат, а які – не можна (зафарбуйте їх у різні кольори). Якщо з точки (0; 0) можна потрапити до точки (x; y), то за скільки ходів це вдасться зробити?

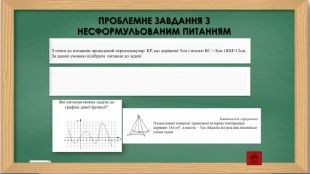
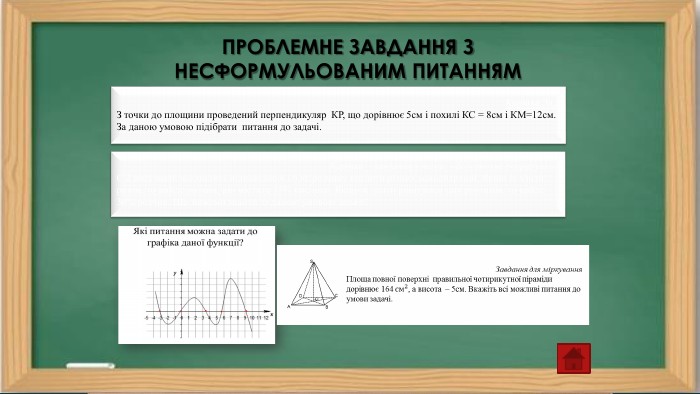
ПРОБЛЕМНЕ ЗАВДАННЯ З НЕСФОРМУЛЬОВАНИМ ПИТАННЯМКартка – завдання з теми: «Відсоткові розрахунки»Є 2 посудини, що містять відповідно 4 і 6 кг розчину кислоти різних концентрацій. Якщо їх злити разом, то вийде розчин, що містить 35% кислоти. Якщо ж злити рівні маси цих розчинів, то вийде 36% розчин. Що можемо знайти за даною умовою задачі?Картка № 3 З точки до площини проведений перпендикуляр КР, що дорівнює 5см і похилі КС = 8см і КМ=12см. За даною умовою підібрати питання до задачі.

Витрати на паливо для пароплава ділиться на частини. Одна з них не залежить від швидкості і дорівнює 480 гривень за годину. А друга частина витрат пропорційна кубу швидкості, причому при швидкості 10 км/годину ця частина витрат дорівнює 30 гривень. Необхідно знайти, при який швидкості сума витрат буде найменшою. Серед 30 деталей є браковані. Яка ймовірність того, що взяті навмання деталі будуть без дефекту?На сторінці текст повинен займати 384см2. Які повинні бути розміри сторінки? ПРОБЛЕМНІ ЗАВДАННЯ З ВІДСУТНІМИ ДАНИМИЯкі розрахунки необхідно знати для крою деталей сумки-бочечки? Оберіть їх самі і знайдіть витрату тканини в кв. метрах.

ПРОБЛЕМНІ ЗАВДАННЯ З КІЛЬКОМА РІШЕННЯМИКартка № 2Є іграшка "ванька- встанька". Неваляшка. На заводі іграшок замислились, а чі можна вдовконалити іргашку, зробити її цікавішою? І знайшли кілька варіантів не змінюючі зовнішність іграшки. А ваші варіанти які будуть? Тема уроку: «Розв'язування вправ»Довжина акваріума 80 см, ширина 45 см, а висота 55 см. Скільки води треба влити в цей акваріум, щоб рівень води був нижче верхнього краю акваріума на 10 см?rrrrr

Висновки Учень неспроможний і не повинен повторювати весь історичний шлях розвитку людського знання. Але принципам цього розвитку та узагальненим способам дії він повинен слідувати для того, щоб засвоювати їх, щоб розвивати способи творчої діяльності. Розглянуто можливості використання проблемного навчання під час уроків математики і на основі цього зроблено висновки у тому, що цей вид навчання необхідний і можливий при навчанні математики в основній школі, що він сприяє розвитку вміння логічно вибудовувати свої відповіді, розвитку творчої та самостійної особистості. Водночас проблемне навчання відповідає вимогам сучасності: навчати, досліджувати, досліджувати навчаючи. Лише так можна формувати творчу особистість, тобто реалізовувати основне завдання педагогічної праці.

Для успішного виконання проблемного завдання на початковому етапі вчителю необхідно: • організувати роботу з навчально-методичною літературою, графічними посібниками (таблицями, схемами, графіками, моделями); • виділити основні категорії та поняття;• розробити як алгоритмічні завдання (покроковий опис методів і прийомів задля досягнення поставленої мети), так і творчо розвиваючі;• рекомендувати роботу з інформаційними комп’ютерними технологіями для забезпечення пошуку та обміну інформацією;• дати можливість учням самим вибирати зручну для них форму роботи – індивідуально, у парах, у малих групах.

Організована подібним чином робота дозволяє учням:• вирішувати певні практичні завдання, що стоять перед ними не лише в рамках даного предмета, але і в різних життєвих ситуаціях;• висувати власні гіпотези, критично оцінювати реальну ситуацію. Необхідність організації навчально-виховної роботи з використанням технології проблемного навчання є особливо важливою для формування пізнавальної самостійності учнів, створюючи основу для їх успішної соціалізації.

Список використаних джерел1. В. Н. Осинський, “Активізація пізнавальної діяльності учнів на уроках математики в 9-10класах”, Київ “Радянська школа”, 1980.2“Дидактика сучасної школи” під редакцією В. А. Онищенка. Київ “радянська школа”,1987.3. В. Г.коваленко, І. Ф. Тесленко, “проблемний підхід до навчання математики”, Київ“Радянська школа”, 1985.4. М. Д. Касьяненко, “підвищення ефективності навчання математики”. Київ “Радянськашкола”, 1980.5. О. Я. Блох, Е. С. Канін та інші, “Методика викладання математики в середній школі.”Харків, “Основа”, 1992.6. «Методика навчання математики», Слепкань З.І.